Đề thi Olympic môn Toán lớp 10 trường THPT Đa Phúc, Hà Nội năm học 2016 - 2017

Đề thi Olympic môn Toán lớp 10

Đề thi Olympic môn Toán lớp 10 trường THPT Đa Phúc, Hà Nội năm học 2016 - 2017 được VnDoc.com sưu tầm và đăng tải, nhằm giúp các em học sinh có tài liệu ôn tập, luyện tập nhằm nắm vững được những kiến thức, kĩ năng cơ bản, đồng thời vận dụng kiến thức để giải các bài tập môn Toán một cách thuận lợi và tự kiểm tra đánh giá kết quả học tập của mình.

Đề thi Olympic truyền thống 30-4 năm 2014 môn Toán lớp 10

Đề thi học sinh giỏi môn Toán lớp 10 trường THPT Con Cuông, Nghệ An năm học 2015 - 2016

SỞ GD & ĐT HÀ NỘI TRƯỜNG THPT ĐA PHÚC

ĐỀ THI OLYMPIC MÔN TOÁN 10 NĂM HỌC 2016 – 2017 (Thời gian làm bài: 120 phút)

Câu 1. (3,5 điểm): Cho hàm số y = x² + 4x + 1 và hàm số y = -2x + m. Tìm m để đồ thị các hàm số đó cắt nhau tại hai điểm phân biệt A, B đồng thời khoảng cách từ trọng tâm G của tam giác OAB đến các trục tọa độ bằng nhau. (điểm O là gốc tọa độ)

Câu 2. (6.5 điểm):

a) Giải hệ phương trình: .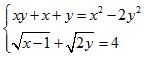

b) Giải phương trình: .

Câu 3. (1,5 điểm): Cho tam giác ABC thỏa mãn hệ thức . (h_b là độ dài đường cao ứng với cạnh AC). Chứng minh tam giác ABC là tam giác cân.

Câu 4. (3,5 điểm): Trong mặt phẳng Oxy, cho điểm A(3;1). Trên trục Ox, Oy lần lượt lấy hai điểm B, C sao cho tam giác ABC vuông tại A. Tìm tọa độ điểm B, C sao cho diện tích tam giác ABC lớn nhất biết hoành độ của điểm B và tung độ của điểm C không âm.

Câu 5. (3,0 điểm): Cho đường tròn tâm O và ba dây cung song song AB, CD, EF của đường tròn đó. Gọi H, I, K lần lượt là trực tâm của các tam giác ACF, AED, CEB. Chứng minh H, I, K thẳng hàng.

Câu 6. (2,0 điểm): Cho a, b, c > 0 thỏa mãn: a² + b² + c² + ab - 2bc - 2ca = 0.

Chứng minh: .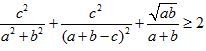

--------------- Hết ------------------

Đáp án đề thi Olympic môn Toán lớp 10