Đề thi học sinh giỏi môn Toán lớp 10 trường THPT Con Cuông, Nghệ An năm học 2015 - 2016

Đề thi học sinh giỏi môn Toán lớp 10

Đề thi học sinh giỏi môn Toán lớp 10 trường THPT Con Cuông, Nghệ An năm học 2015 - 2016 là đề thi học sinh giỏi cấp trường bậc THPT được VnDoc.com sưu tầm và đăng tải. Đây là tài liệu hữu ích dành cho các bạn học sinh lớp 10 luyện đề, ôn thi học sinh giỏi môn Toán. Chúc các bạn đạt kết quả cao trong các bài thi sắp tới.

Đề thi HSG môn Toán lớp 10 trường THPT Tam Quan năm 2015 -2016

Đề thi học sinh giỏi lớp 10 THPT tỉnh Thái Nguyên năm 2011 - 2012

Đề thi học sinh giỏi môn Toán lớp 10 trường THPT Lý Thái Tổ, Bắc Ninh năm học 2015 - 2016

SỞ GD & ĐT NGHỆ AN TRƯỜNG THPT CON CUÔNG ĐỀ CHÍNH THỨC

ĐỀ THI HỌC SINH GIỎI CẤP TRƯỜNG KHỐI 10 NĂM HỌC 2015 – 2016 Môn: TOÁN Thời gian: 150 phút (không kể thời gian phát đề)

Câu 1. (5,0 điểm) Cho phương trình: (m - 2)x² - (2m + 1)x + 3m - 3 = 0 (1)

a) Giải phương trình (1) khi m = 3.

b) Giả sử x₁, x₂ là hai nghiệm của phương trình (1). Tìm m sao cho (2m + 1)x₁ + (m - 2)x₂² = m - 2

Câu 2. (3,0 điểm) Giải phương trình:

Câu 3. (2,0 điểm) Cho a,b là các số thực thỏa mãn: a, b ∈ [1/4; 2] và a + b = 4ab. Tìm giá trị lớn nhất của biểu thức:

P = (a - b)² - 2(a + b)

Câu 4. (3,0 điểm) Cho sinα + cosα = √6/2, α ∈ (0; π/4). Tính giá trị biểu thức sau:

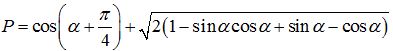
Câu 5. (4,0 điểm) Cho tam giác ABC. Điểm M thuộc cạnh BC sao cho MC = 3MB, I là điểm thuộc đoạn AM sao cho AI = 3IM. Xác định điểm K thuộc cạnh AC sao cho ba điểm B, I, K thẳng hàng.

Câu 6. (3,0 điểm) Trong mặt phẳng với hệ tọa độ Oxy, cho tam giác ABC có A(2; 6), đường phân giác trong của góc A cắt cạnh BC tại D(2; -3/2). Viết phương trình cạnh BC. Biết đường tròn ngoại tiếp tam giác AC có phương trình: x² + y² + x - 2y - 30 = 0.

Đáp án đề thi học sinh giỏi môn Toán lớp 10