Đề thi thử Quốc gia lần 2 năm 2015 môn Toán trường THPT Sông Lô, Tuyên Quang
Đề thi thử Quốc gia lần 2 năm 2015 môn Toán trường THPT Sông Lô, Tuyên Quang là đề luyện thi đại học môn Toán, thi thử đại học môn Toán có đáp án dành cho các bạn học sinh và thầy cô giáo tham khảo, nghiên cứu chuẩn bị cho kì thi THPT Quốc gia môn Toán.
Đề thi thử Quốc gia môn Toán
| TRƯỜNG THPT SÔNG LÔ (Đề thi có 01 trang) |
ĐỀ KTCL ÔN THI THPT QUỐC GIA LẦN 2 NĂM 2015 Môn thi : TOÁN Thời gian làm bài: 180 phút, không kể thời gian phát đề |
Câu 1 (2,0 điểm). Cho hàm số:
| y = | x + 2 | (1) |
| x - 1 |
a. Khảo sát sự biến thiên và vẽ đồ thị (H) của hàm số (1).
b. Viết phương trình tiếp tuyến của đồ thị hàm số tại giao điểm của đồ thị và đường thẳng y = 4.
Câu 2 (1,0 điểm).
a. Giải phương trình: cos2x + 7cosx + 4 = 0 .
b. Một hộp có 7 bút bi xanh, 8 bút bi đỏ và 5 bút bi đen chỉ khác nhau về màu, lấy ngẫu nhiên từ hộp trên 3 bút bi. Tính xác suất để trong 3 bút lấy ra có đủ 3 màu.
Câu 3 (1,0 điểm). Tìm giá trị lớn nhất và nhỏ nhất của hàm số trên đoạn [-0,5; 2]:

Câu 4 (1 điểm). Tính diện tích hình phẳng giới hạn bởi đồ thị các hàm số: y = x2 + x - 1 và y = x4 + x - 1.
Câu 5 (1,0 điểm). Trong không gian với hệ tọa độ Oxyz, cho bốn điểm A (-1;1;2), B(1;0;1), C(-1;1;0) và D (2;-1; -2).
a. Viết phương trình mặt phẳng (P) đi qua ba điểm B, C, D.
b. Viết phương trình mặt cầu (S) có tâm A và tiếp xúc với mặt phẳng (P).
Câu 6 (1 điểm). Cho hình chóp đều S.ABCD có cạnh bên và cạnh đáy cùng bằng a , gọi M là trung điểm của SC. Một mặt phẳng (P) chứa AM và song song với BD, lần lượt cắt SB, SD tại I K. Tính theo a thể tích khối đa diện SMIAK.
Câu 7 (1,0 điểm). Trong mặt phẳng Oxy, cho tam giác ABC cân tại A, phương trình đường trung tuyến kẻ từ đỉnh A là (d) 2x + y -3 = 0. Biết đỉnh B thuộc trục hoành, đỉnh C thuộc trục tung và diện tích tam giác ABC bằng 5. Tìm toạ độ các đỉnh A, B, C của tam giác ABC.

Đáp án đề thi thử Quốc gia môn Toán
| TRƯỜNG THPT SÔNG LÔ (HD chấm có 05 trang) |
HƯỚNG DẪN CHẤM KTCL ÔN THI THPTQG LẦN 2 NĂM 2015 Môn thi : TOÁN |
I. LƯU Ý CHUNG
- Hướng dẫn chấm chỉ trình bày một cách giải với những ý cơ bản phải có. Khi chấm bài học sinh làm theo cách khác nếu đúng và đủ ý thì vẫn cho điểm tối đa.
- Điểm toàn bài tính đến 0,25 và không làm tròn.
- Với bài hình học không gian (câu 6) nếu thí sinh không vẽ hình hoặc vẽ sai ở phần nào thì không cho điểm tương ứng với phần đó.
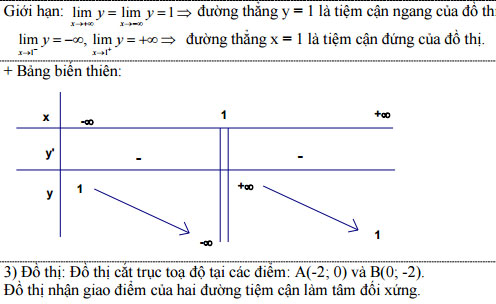
Câu 1: Cho hàm số y = (x + 2)/(x - 1) (1)
Khảo sát sự biến thiên và vẽ đồ thị (H) hàm số (1)
1) Tập xác định D = R\ {1}.
2) Sự biến thiên:
+) y' = -3/(x - 1)2 < 0, với mọi x thuộc D suy ra hàm số nghịch biến trên từng khoảng xác định. Hàm số không có cực trị.

b, Viết phương trình tiếp tuyến của đồ thị hàm số tại giao điểm của đồ thị và đường thẳng y = 4.
Phương trình hoành độ giao điểm y = (x + 2)/(x - 1) = 4
- x ≠ 1
- (x + 2) = 4(x - 1)
Giải ra ta được x ≠ 1, và x = 2 suy ra x = 2 suy ra M(2; 4) là giao điểm của đồ thị và đường thẳng y = 4.
Xét phương trình y' = -3/(x-1)2, hệ số góc tiếp tuyến tại điểm M(2; 4) là k = y'(2) = -3/(2 - 1)2 = -3
Phương trình tiếp tuyến là y = -3(x - 2) + 4 ↔ y = -3x + 10.
Câu 2:
a, Giải phương trình cos2x + 7cosx + 4 = 0
↔ 2cos²x + 7cosx + 3 = 0 ↔ cosx = -0,5
hoặc cosx = -3.
Suy ra cosx = -0.5 ↔ x = ± 2π/3 + k2π, k thuộc N.


