Đề thi thử THPT Quốc gia năm 2016 môn Toán trường THPT Lê Lợi, Thanh Hóa (Lần 1)

Đề thi thử THPT Quốc gia năm 2016 môn Toán

Đề thi thử THPT Quốc gia năm 2016 môn Toán trường THPT Lê Lợi, Thanh Hóa (Lần 1) có đáp án đi kèm, được VnDoc.com sưu tầm và đăng tải với hy vọng giúp các bạn học sinh ôn tập và nâng cao kiến thức môn Toán hiệu quả, từ đó chuẩn bị tốt nhất cho kì thi THPT Quốc gia 2016 sắp tới. Mời các bạn tham khảo.

Tuyển tập 20 đề thi thử THPT Quốc gia môn Toán năm 2016

Bộ đề thi thử THPT Quốc gia năm 2016 môn Toán - Số 1

Bộ đề thi thử THPT Quốc gia năm 2016 môn Toán - Số 2

SỞ GIÁO DỤC & ĐÀO TẠO THANH HÓA TRƯỜNG THPT LÊ LỢI

ĐỀ THI KSCL CÁC MÔN THI TỐT NGHIỆP THPT QUỐC GIA LẦN 1 NĂM HỌC 2015 -2016 Môn: Toán – lớp 12 (Thời gian làm bài: 180 phút, không kể giao đề)

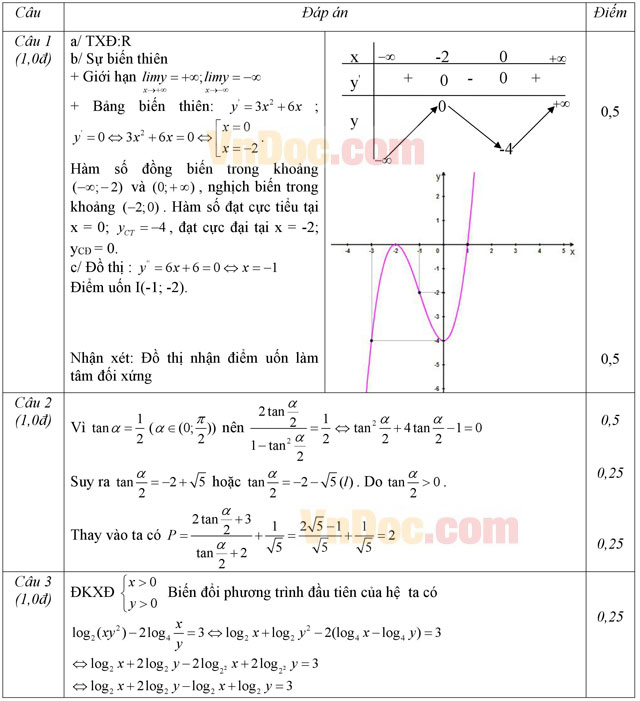
Câu 1. (1,0 điểm) Khảo sát sự biến thiên và vẽ đồ thị hàm số y = f(x) = x³ + 3x² - 4.

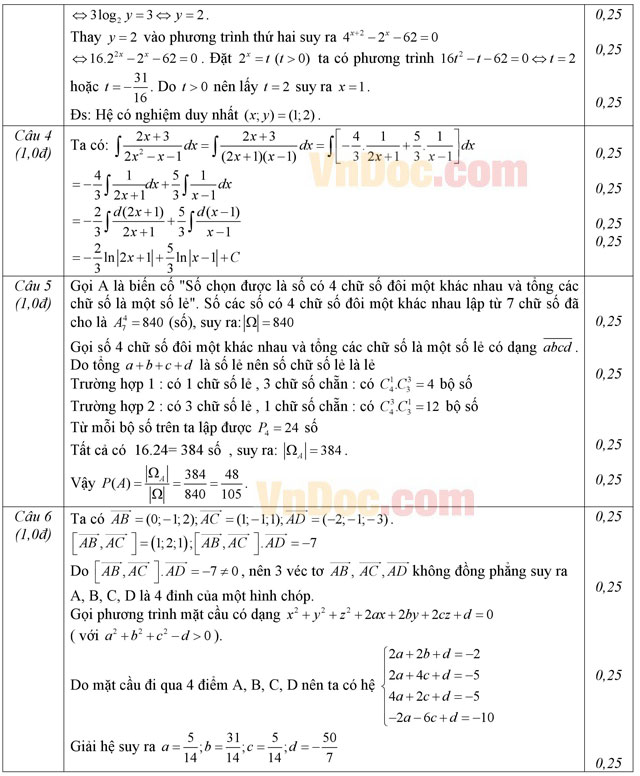
Câu 2. (1,0 điểm) Cho tanα = 1/2 (α ∈ (0; π/2)). Tính giá trị biểu thức:

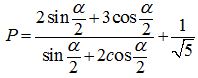
Câu 3. (1,0 điểm) Giải hệ phương trình .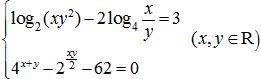

Câu 4. (1,0 điểm) Tìm họ nguyên hàm

Câu 5. (1,0 điểm) Gọi M là tập hợp các số có 4 chữ số đôi một khác nhau lập từ các chữ số 1, 2, 3, 4, 5, 6, 7. Lấy ra từ tập M một số bất kỳ. Tính xác suất để lấy được số có tổng các chữ số là số lẻ ?

Câu 6. (1,0 điểm) Trong không gian với hệ tọa độ Oxyz cho 4 điểm A(1; 1; 0); B(1; 0; 2); C(2;0; 1), D(-1; 0; -3). Chứng minh A, B, C, D là 4 đỉnh của một hình chóp và viết phương trình mặt cầu ngoại tiếp hình chóp đó .

Câu 7. (1,0 điểm) Cho hình chóp S.ABC có tam giác ABC vuông tại A, BC = 2a, góc ABC = 60⁰. Mặt phẳng (SAB) vuông góc với mp(ABC), tam giác SAB cân tại S, tam giác SBC vuông tại S. Tính thể tích khối chóp S.ABC và khoảng cách từ điểm A tới mp(SBC).

Câu 8. (1,0 điểm) Cho tam giác ABC. Đường phân giác trong của góc B có phương trình d₁: x + y - 2 = 0, đường trung tuyến kẻ từ B có phương trình d₂: 4x + 5y - 9 = 0. Đường thẳng chứa cạnh AB đi qua điểm M(2; 1/2), bán kính đường tròn ngoại tiếp tam giác ABC là R = 5/2. Tìm tọa độ đỉnh A .

Câu 9. (1,0 điểm) Giải phương trình sau trên tập số thực .

Câu 10. (1,0 điểm) Cho là các số thực thuộc đoạn [0; 1]. Tìm giá trị lớn nhất của biểu thức P = 2(x³ + y³ + x³) - (x²y + y²z + z²x)

Đáp án đề thi thử THPT Quốc gia năm 2016 môn Toán