Đề thi tuyển sinh vào lớp 10 THPT môn Toán trường PTNK, Đại Học Quốc Gia TP. HCM năm 2016 - 2017

Đề thi tuyển sinh vào lớp 10 THPT môn Toán

Đề thi tuyển sinh vào lớp 10 THPT môn Toán trường PTNK, Đại Học Quốc Gia TP. HCM năm 2016 - 2017 được VnDoc sưu tầm và đăng tải nhằm giúp các em học sinh có thêm nhiều tài liệu ôn thi vào lớp 10 môn Toán để tham khảo chuẩn bị tốt cho kì thi tuyển sinh sắp tới đây đạt kết quả cao. Mời các em cùng tham khảo.

Đề thi tuyển sinh vào lớp 10 THPT môn Toán sở GD&ĐT Hải Dương năm 2016 - 2017

Đề thi tuyển sinh vào lớp 10 THPT môn Toán sở GD&ĐT Hưng Yên năm 2016 - 2017

Đề thi tuyển sinh vào lớp 10 THPT môn Ngữ văn trường THPT Chuyên Lam Sơn, Thanh Hóa năm 2016 - 2017

ĐẠI HỌC QUỐC GIA TP. HCM TRƯỜNG PHỔ THÔNG NĂNG KHIẾU

ĐỀ THI TUYỂN SINH LỚP 10 Năm học: 2016 - 2017 Môn thi: Toán (không chuyên) Thời gian: 120 phút, không kể thời gian phát đề

Bài 1 (1 điểm) Biết a và b là các số dương, a ≠ b và

Tính S = a + b

Bài 2 (2 điểm)

a) Giải phương trình

b) Giải hệ phương trình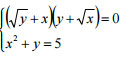

Bài 3 (2 điểm) Cho phương trình

b) Giải phương trình (1) khi m = -8

b) Tìm m để phương trình (1) có 2 nghiệm phân biệt x₁, x₂ sao cho

Bài 4 (2 điểm)

a) Ông An định cải tạo một mảnh vườn hình chữ nhật có chiều dài bằng 2,5 lần chiều rộng. Ông thấy rằng nếu đào một cái hồ có mặt hồ là hình chữ nhật thì sẽ chiếm mất 3% diện tích mảnh vườn, còn nếu giảm chiều dài 5m và tăng chiều rộng 2m thì mặt hồ là hình vuông là diện tích mặt hồ giảm đươkc 20m². Hãy tính các cạnh của mảnh vườn.

b) Lớp 9A có 27 học sinh nam và 18 học sinh nữ. Nhân dịp sinh nhật của bạn X (là một thành viên của lớp), các bạn trong lớp có rất nhiều món quà tặng X. Ngoài ra mỗi bạn nam của lớp làm 3 tấp thiệp và mỗi bạn nữ xếp 2 hoặc 5 con hạc để tặng bạn X. Biết số tấm thiệp và số con hạc bằng nhau, hỏi bạn X là nam hay nữ?

Bài 5 (3 điểm) Tam giác đều ABC có tâm 0, AB = 6a và các điểm M, N lần lượt thuộc các cạnh AB, AC mà AM = AN = 2a. Gọi I, J, K lần lượt là trung điểm của BC, AC và MN.

a) Chứng minh các điểm M, N, B, C cùng thuộc một đường tròn T. Tính diện tích tứ giác BMNC theo a

b) Tính bán kính đường tròn ngoại tiếp tam giác IJK. Chứng minh đường tròn đường kính NC tiếp xúc với AI.

c) AE tiếp xúc với đường tròn T tại E (E và B cùng phía đối với đường thẳng AI). Gọi F là trung điểm của OE, tính số đo của góc AFJ.

Đáp án đề thi tuyển sinh vào lớp 10 THPT môn Toán