Đề kiểm tra học kì 1 môn Toán lớp 10 năm học 2015 - 2016 trường THPT Nguyễn Trung Trực

Đề kiểm tra học kì 1 môn Toán lớp 10

Đề kiểm tra học kì 1 môn Toán lớp 10 năm học 2015 - 2016 trường THPT Nguyễn Trung Trực là tài liệu học tập hay được VnDoc.com sưu tầm và tổng hợp. Đề thi học kì 1 lớp 10 môn toán cơ bản này nhằm giúp các em học sinh ôn tập và củng cố kiến thức hiệu quả, đồng thời làm quen với cấu trúc đề năm nay. Mời các em cùng tham khảo.

Đề cương ôn tập học kì 1 môn Toán lớp 10 trường THPT Đa Phúc, Hà Nội năm học 2016 - 2017

Đề kiểm tra học kì 1 môn Hóa học lớp 10 năm học 2015 - 2016 trường THPT Thăng Long

Đề kiểm tra học kì 1 môn Tiếng Anh lớp 10 trường THPT Đoàn Thượng, Hải Dương năm 2014 - 2015

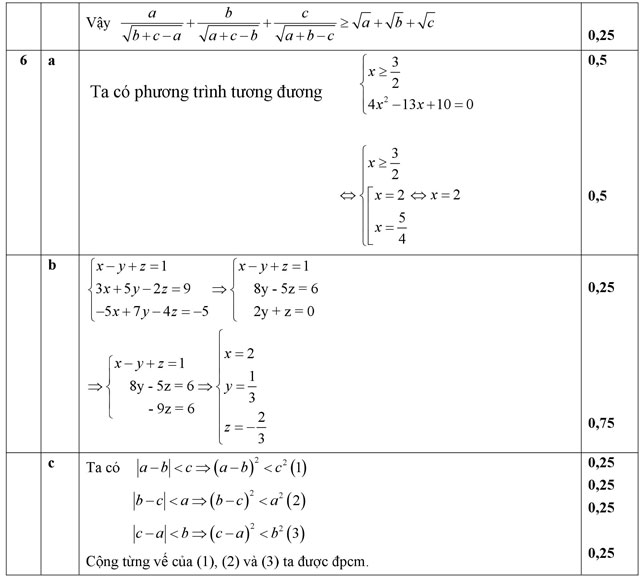
Trường THPT Nguyễn Trung Trực

ĐỀ THI HỌC KỲ I NĂM HỌC 2015-2016 MÔN: TOÁN – LỚP 10 Thời gian làm bài: 90 phút

A. PHẦN CHUNG CHO TẤT CẢ THÍ SINH (7 điểm)

Bài 1: (1,0 điểm) Nêu mệnh đề phủ định của mệnh đề sau, xét xem mệnh đề phủ định đó đúng hay sai:

a) Phương trình x² - 4x + 3 = 0 có nghiệm. b) 2²⁰¹¹ chia hết cho 8

c) Có vô số số nguyên tố chia hết cho 3. d) x² + x + 1 ≤ 0

Bài 2: (2,0 điểm)

a) Cho A = {n ∈ N*/ n < 6} và B = {0; 1; 4; 5; 7}. Xác định A ∩ B và B\A

b) Tìm tập xác định của hàm số

Bài 3: (2,0 điểm) Cho hàm số y = ax² + bx + 3

a) Xác định a, b của hàm số biết đồ thị hàm số đi qua A(1;0) và B(-2;15)

b) Lập bảng biến thiên và vẽ đồ thị hàm số vừa tìm được ở câu a.

Bài 4: (2,0 điểm)

a) Cho ba điểm A(3; 2), B(4; 1) và C(1; 5). Tìm toạ độ trọng tâm G của tam giác ABC và tìm tọa độ của điểm M để ABCM là hình bình hành.

b) Cho sinα = 4/5 (0⁰ < α < 90⁰). Tính giá trị của biểu thức

B. PHẦN RIÊNG (3 điểm)

Bài 5 (Dành cho thí sinh học chương trình nâng cao)

a/ (1,0 điểm) Giải phương trình:

b/ (1,0 điểm) Giải hệ phương trình

c/ (1,0 điểm) Chứng minh rằng nếu a, b, c là độ dài các cạnh của một tam giác thì ta luôn có

Bài 6 (Dành cho thí sinh học chương trình cơ bản)

a/ (1,0 điểm) Giải phương trình:

b/ (1,0 điểm) Giải hệ phương trình: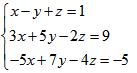

c/ (1,0 điểm) Chứng minh rằng nếu a, b, c là độ dài các cạnh của một tam giác thì ta luôn có

a² + b² + c² < 2(ab + bc + ca)

Đáp án đề kiểm tra học kì 1 môn Toán lớp 10