Đề thi chọn học sinh giỏi Toán 12 cấp tỉnh năm 2018 - 2019 Sở GD&ĐT Hải Dương
Đề thi chọn học sinh giỏi Toán 12 có đáp án
SỞ GIÁO DỤC VÀ ĐÀO TẠO
HẢI DƯƠNG
(Đề thi gồm 01 trang)
KỲ THI CHỌN HỌC SINH GIỎI TỈNH LỚP 12 THPT
Năm học 2018-2019
Môn thi: TOÁN
Ngày thi: 04 tháng 10 năm 2018
Thời gian làm bài: 180 phút
Câu I (2,0 điểm)
1) Cho hàm số
21
1
x
y
x
−
=
+
có đồ thị
( )
C
. Tìm
m
để đường thẳng
:dy xm=−+
cắt
( )
C
tại hai
điểm phân biệt
A
và
B
sao cho
PAB
∆
đều, biết
( )
2;5P
.
2) Một mảnh đất hình chữ nhật
ABCD
có chiều dài
25AB m=
, chiều rộng
20AD m=
được
chia thành hai phần bằng nhau bởi vạch chắn
MN
(
, MN
lần lượt là trung điểm
BC
và
AD
).
Một đội xây dựng làm một con đường đi từ
A
đến
C
qua vạch chắn
MN
, biết khi làm đường
trên miền
ABMN
mỗi giờ làm được
15m
và khi làm trong miền
CDNM
mỗi giờ làm được
30m
.
Tính thời gian ngắn nhất mà đội xây dựng làm được con đường đi từ
A
đến
C
.
Câu II (2,0 điểm)
1) Giải hệ phương trình
22
(31)4 431
.
3 4 42 3
x yy x
xy x x
++ =+ +
= ++ +
2) Trong cuộc thi: "Thiết kế và trình diễn các trang phục dân tộc" do Đoàn trường THPT tổ
chức vào tháng 3 năm 2018 với thể lệ mỗi lớp tham gia một tiết mục. Kết quả có 12 tiết mục
đạt giải trong đó có 4 tiết mục khối 12, có 5 tiết mục khối 11và 3 tiết mục khối 10. Ban tổ chức
chọn ngẫu nhiên 5 tiết mục biểu diễn chào mừng 26 tháng 3. Tính xác suất sao cho khối nào
cũng có tiết mục được biểu diễn và trong đó có ít nhất hai tiết mục của khối 12.
Câu III (2,0 điểm)
1) Cho dãy số
( )
n
u
xác định bởi
2
11
11
1, , 1
n
n
n
u
uu n
u
+
+−
= = ∀≥
. Xét tính đơn điệu và bị chặn
của
( )
n
u
.
2) Trong mặt phẳng với hệ tọa độ
Oxy
, cho hình thang cân
ABCD
( // , )AB CD AB CD>
có
AD DC=
,
(3;3)D
. Đường thẳng
AC
có phương trình
20xy−−=
, đường thẳng
AB
đi qua
( 1; 1)M −−
. Viết phương trình đường thẳng
BC
.
Câu IV (3,0 điểm)
Cho hình hộp đứng
.’’’’ABCD A B C D
có đáy
ABCD
là hình vuông .
1) Gọi
S
là tâm của hình vuông
''''ABCD
.
SA
,
BC
có trung điểm lần lượt là
M
và
N
.
Tính thể tích của khối chóp
.S ABC
theo
a
, biết
MN
tạo với mặt phẳng
()ABCD
một góc bằng
60
0
và
AB a=
.
2) Khi
'AA AB=
. Gọi
,RS
lần lượt nằm trên các đoạn thẳng
’ , ’A D CD
sao cho
RS
vuông
góc với mặt phẳng
( ' ')CB D
và
3
3
a
RS =
. Tính thể tích khối hộp
.’’’’ABCD A B C D
theo
a
.
3) Cho
'AA AB a= =
. Gọi
G
là trung điểm
'BD
, một
( )
mp P
thay đổi luôn đi qua
G
cắt các
đoạn thẳng
', ', ' 'AD CD D B
tương ứng tại
,,HIK
. Tìm giá trị lớn nhất của biểu thức
111
'.' '.' '.'
T
DHDI DIDK DKDH
=++
.
Câu V (1,0 điểm)
Cho các số dương
,,abc
. Tìm giá trị nhỏ nhất của biểu thức
3
16
P
a ab abc a b c
= −
+ + ++
.
--- Hết ---
Họ và tên thí sinh: ....................................................................... Số báo danh: .........................
Chữ kí giám thị coi thi số 1: .................................. Chữ kí giám thị coi thi số 2: .........................
ĐỀ CHÍNH THỨC
SỞ GIÁO DỤC VÀ ĐÀO TẠO
HẢI DƯƠNG
HƯỚNG DẪN CHẤM
ĐỀ THI CHỌN HỌC SINH GIỎI TỈNH LỚP 12 THPT
Năm học 2018-2019
Môn thi: TOÁN
(Hướng dẫn chấm gồm 06 trang)
Câu
Nội dung
Điểm
Câu I.1
1,0 đ
Cho hàm số
21
1
x
y
x
−
=
+
có đồ thị
( )
C
. Tìm
m
để đường thẳng
:dy xm=−+
cắt
( )
C
tại hai điểm phân biệt
A
và
B
sao cho
PAB
∆
đều, biết
(
)
2;5
P
.
hoành độ giao điểm của đường thẳng
d
và đồ thị
()C
là nghiệm phương trình
21
1
x
xm
x
−
=−+ ⇔
+
(
)
2
( 3) 1 0 1
x m xm− − − −=
(
1x = −
không là nghiệm của (1))
0,25
Đường thẳng
d
cắt đồ thị
(C)
tại hai điểm phân biệt khi và chỉ khi phương trình
( )
1
có hai
nghiệm phân biệt
2
0 2 13 0
mm m⇔∆>⇔ − + >⇔ ∈
0,25
Gọi
12
,xx
là các nghiệm của phương trình (1), ta có:
12
12
3
1
xx m
xx m
+=−
=−−
Giả sử
( )
11
;Ax x m−+
,
( )
22
;
Bx x m
−+
Khi đó ta có:
(
)
2
12
2AB x x
= −
( ) ( )
( ) ( )
2 2 22
1 1 12
2 5 22PA x x m x x= −+−+−= −+−
,
( ) ( ) ( ) ( )
2 2 22
2 2 21
2 5 22PB x x m x x= −+−+−= −+−
Suy ra
PAB
∆
cân tại
P
0,25
Do đó
PAB∆
đều
22
PA AB⇔=
( )
( ) ( ) ( )
( )
22 2 2
1 2 12 12 12 12
2 2 2 4 6 80x x xx xx xx xx⇔−+−= − ⇔+ + +− −=
2
1
4 50
5
m
mm
m
=
⇔ + −=⇔
= −
. Vậy giá trị cần tìm là
1, 5mm= = −
.
0,25
Câu I.2
1,0 đ
Một mảnh đất hình chữ nhật
ABCD
có chiều dài
25AB m=
, chiều rộng
20AD m=
được chia thành hai phần bằng nhau bởi vạch chắn
MN
(
, MN
lần lượt là
trung điểm
BC
và
AD
). Một đội xây dựng làm một con đường đi từ
A
đến
C
qua vạch
chắn
MN
, biết khi làm đường trên miền
ABMN
mỗi giờ làm được
15m
và
khi làm
trong miền
CDNM
mỗi giờ làm được
30m
. Tính thời gian ngắn nhất mà đội xây dựng
làm được con đường đi từ
A
đến
C
.
Giả sử con đường đi từ A đến C gặp vạch chắn MN tại E
đặt
22
( )( [0;25]) 10 ;NE x m x AE x= ∈ ⇒= +
22
(25 ) 10CE x= −+
0,25
Thời gian làm đường đi từ A đến C là
2
2
(25 ) 100
100
() ()
15 30 15 30
x
AE CE x
tx h
−+
+
=+= +
0,25
22
(25 )
'( ) ;
15 100 30 (25 ) 100
xx
tx
xx
−
= −
+ −+
0,25
x
25m
20m
N
D
M
B
C
A
E
22
'( ) 0 2 (25 ) 100 (25 ) 100tx x x x x=⇔ −+ =− +
2 2 22
(25 ) 0
4 [(25 ) 100] (25 ) ( 100)
xx
x x xx
−≥
⇔
−+ =− +
22 2 2 2 2
0 25 0 25
4(25 ) ( 25) [400 (25 ) ]=0 ( 5)[4(25 ) ( 5) (45 )]=0
xx
xx x x x xx x x
≤≤ ≤≤
⇔⇔
− −+ −− − − ++ −
5;x⇔=
20 725 10 2 725 2 5
(0) , (25) , (5)
30 30 3
tt t
++
= = = ⇒
Thời gian ngắn nhất làm con đường từ
A đến C là
25
3
(giờ).
0,25
CâuII.1
1,0 đ
Giải hệ phương trình
22
(3 1) 4 4 3 1 (1)
3 4 4 2 3 (2)
x yy x
xy x x
++ =+ +
= ++ +
Điều kiện
0
1
3
y
x
≥
≥−
.
22
(1) (3 1) 4 3 1 4 (*)x xyy⇔ + − += −
xét hàm số
4
( ) 4 ( [0; ));ft t tt= − ∈ +∞
từ (*) ta có
( 3 1) ( )
f x fy+=
3
'( ) 4 4; '( ) 0 1ft t ft t= − =⇔=
bảng biến thiên
-
+
-
0
f(t)
f'(t)
+
∞
1
0
t
0,25
Từ bảng biến thiên ta thấy : hàm số nghịch biến trên
[0;1]
; đồng biến trên
[1; )+∞
+ Nếu
31x+
và
y
cùng thuộc
[0;1]
hoặc
[1; )+∞
thì ta có
31 31
x y yx
+= ⇔ = +
thay vào (2) ta có
0,25
2
3 31 1
3(3 1)4 42 3 9 42 3
4
3 31
xx x
xxxxxxx
y
xx
= ++ =
+ = ++ +⇔ =++ +⇔ ⇔
=
=− +−
(thỏa
mãn)
0,25
+Nếu
31
x +
và
y
không cùng thuộc
[0;1]
hoặc
[1; )+∞
thì
( )
( )
31
3 1 1 1 0 . 0 ( 1) 0
3 11 1
xy
x y xy
xy
−
+− −≤⇔ ≤⇔ −≤
++ +
từ (2)
2
3 ( 1) ( 3 1) 0xy x⇔ − = ++ >
vô lý. Vậy hệ có 2 nghiệm
(; )xy
là
(1; 4)
0,25
CâuII.2
1,0 đ
Trong cuộc thi: "Thiết kế và trình diễn các trang phục dân tộc" do Đoàn trường THPT tổ
chức vào tháng 3 năm 2018 với thể lệ mỗi lớp tham gia một tiết mục. Kết quả có 12 tiết mục
đạt giải trong đó có 4 tiết mục khối 12, có 5 tiết mục khối 11và 3 tiết mục khối 10. Ban tổ
chức chọn ngẫu nhiên 5 tiết mục biểu diễn chào mừng 26 tháng 3. Tính xác suất sao cho khối
nào cũng có tiết mục được biểu diễn và trong đó có ít nhất hai tiết mục của khối 12.
Gọi không gian mẫu của phép chọn ngẫu nhiên là
Ω
Số phần tử của không gian mẫu là: n(
Ω
)=
5
12
792C =
0,25
Gọi A là biến cố “ Chọn 5 tiết mục sao cho khối nào cũng có tiết mục được biểu diễn và
trong đó có ít nhất hai tiết mục của khối 12''
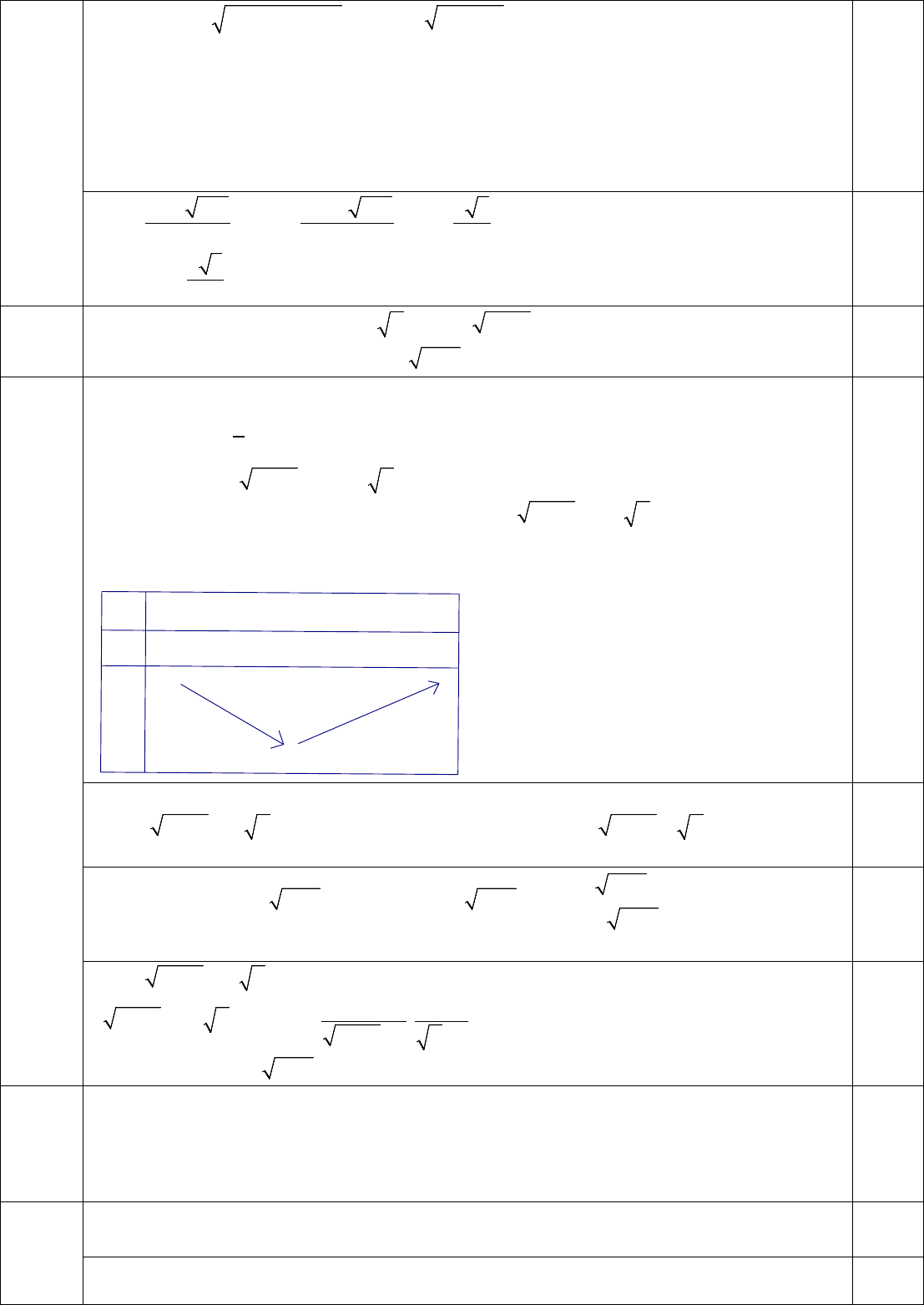
Đề thi chọn học sinh giỏi Toán 12 cấp tỉnh năm 2018 - 2019
VnDoc xin giới thiệu tới bạn đọc tài liệu Đề thi chọn học sinh giỏi Toán 12 cấp tỉnh năm 2018 - 2019 Sở GD&ĐT Hải Dương, nội dung tài liệu gồm 4 câu hỏi bài tập, thời gian làm bài 180 phút, đề thi có đáp án. Mời thầy cô và các bạn học sinh cùng tham khảo.
Đề thi chọn đội tuyển học sinh giỏi THPT môn Toán năm 2018 - 2019 sở GD&ĐT TP. HCM
Đề thi chọn học sinh giỏi cấp tỉnh môn Toán 12 năm 2018 Sở GD&ĐT Bà Rịa - Vũng Tàu
Đề thi chọn học sinh giỏi môn Toán 12 năm học 2017 - 2018 Sở GD&ĐT Nam Định
Đề thi học sinh giỏi lớp 12 môn Toán năm học 2017 - 2018 tỉnh Hải Dương
---------------------------
Để có kết quả cao hơn trong học tập, VnDoc xin giới thiệu tới các bạn học sinh tài liệu Giải bài tập Toán lớp 12, Giải bài tập Hóa học lớp 12, Giải bài tập Vật Lí 12 mà VnDoc tổng hợp và đăng tải.
