Đề thi học kì 1 môn Toán lớp 11 trường THPT Lê Hồng Phong, Đăk Lăk năm học 2015 - 2016
Đề thi học kì 1 môn Toán lớp 11
Đề thi học kì 1 môn Toán lớp 11 trường THPT Lê Hồng Phong, Đăk Lăk năm học 2015 - 2016. Đề thi do các thầy cô giáo thuộc tổ Toán trường THPT Lê Hồng Phong biên soạn. Nội dung kiến thức bám sát SGK Toán lớp 11 học kì 1. Mời các bạn tham khảo.
Đề thi học kì 1 môn Toán lớp 11 trường THPT Nguyễn Hữu Thọ, Long An năm học 2015 - 2016
Đề thi học kì 1 môn Toán lớp 11 trường THPT Tháp Chàm, Ninh Thuận năm học 2015 - 2016
| SỞ GD&ĐT ĐĂK LĂK TRƯỜNG THPT LÊ HỒNG PHONG |
ĐỀ THI HỌC KÌ 1 NĂM HỌC 2015 - 2016 MÔN: TOÁN - LỚP 11 Thời gian làm bài: 90 phút |
Câu 1 (2.0 điểm)
Cho dãy số (Un) được xác định bởi số hạng tổng quát: un = 2n + 1 với 
a. Tìm 5 số hạng đầu của dãy số đã cho.
b. Chứng minh rằng dãy số (Un) là một cấp số cộng. Hãy tính tổng 10 số hạng đầu của cấp số cộng đó.
Câu 2 (1.0 điểm)
Trường THPT Lê Hồng Phong có ba công trình cần thi công là Sân trường, Cổng trường và Tượng đài Lê Hồng Phong. Bộ phận quản lý đã mời đến ba đơn vị thi công là Lê Mạnh, Lê Minh, Lê Huy, chọn ngẫu nhiên một công trình và một đơn vị thi công. Hãy tính xác suất để đơn vị thi công Lê Mạnh nhận được công trình Tượng đài Lê Hồng Phong.
Câu 3 (1.0 điểm)
Giải phương trình 
Câu 4 (2.0 điểm)
Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của AC và BC. Trên đoạn BD lấy điểm P sao cho BP > PD
a. Tìm giao điểm của đường thẳng CD và mặt phẳng (MNP)
b. Chứng minh rằng MN song song với mặt phẳng (ABD)
Câu 5 (2.0 điểm)
Cho hình chóp S.ABCD có đáy ABCD là một tứ giác lồi. Gọi K là điểm thuộc cạnh SA. M, N là hai điểm thuộc lần lượt hai cạnh AC và SB sao cho 
. Với K không trùng với S và A, 
và 
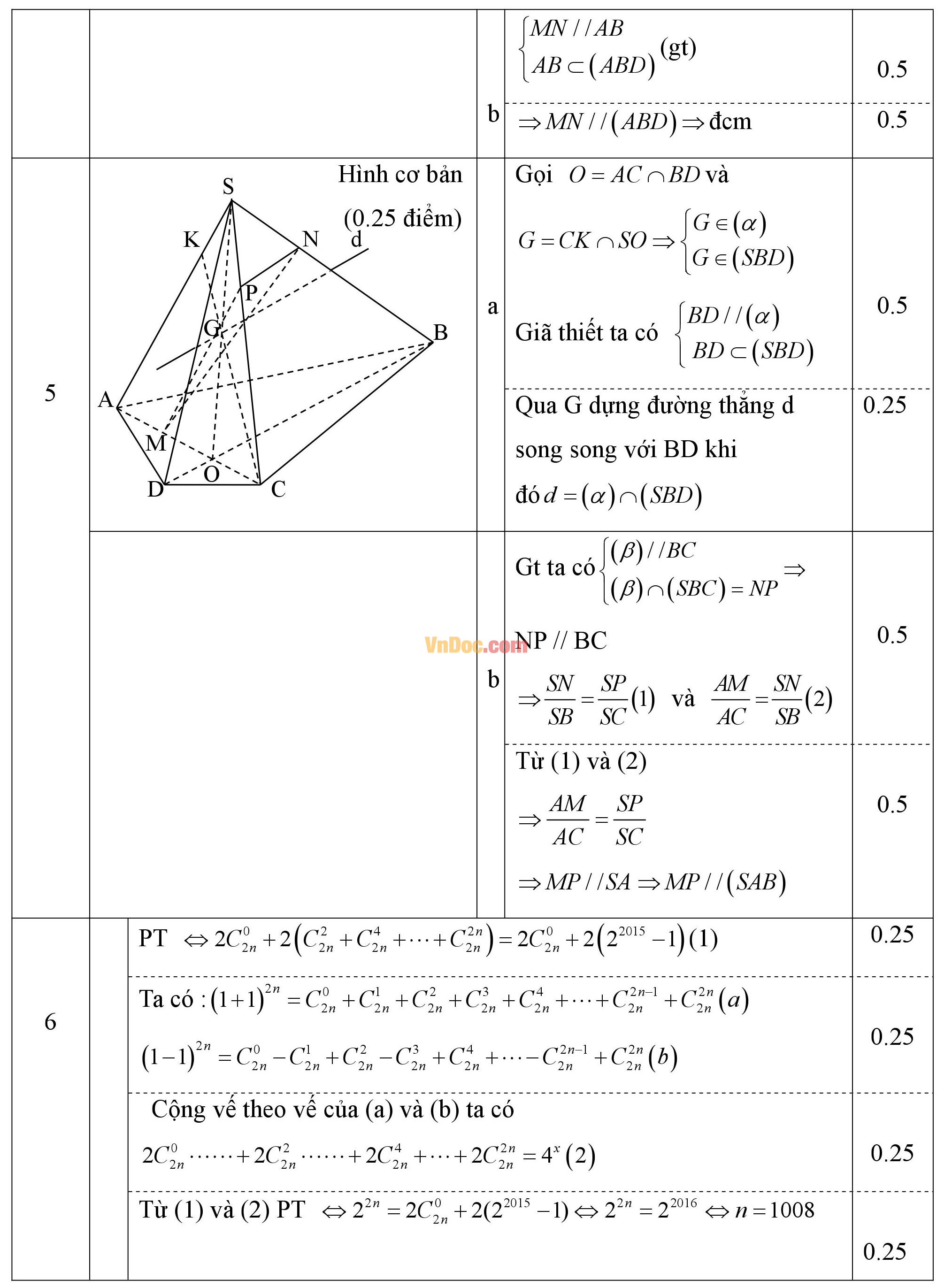
a. Gọi (α) là mặt phẳng chứa CK và song song với đường thẳng BD. Hãy tìm giao tuyến của hai mặt phẳng (α) và (SBD).
b. Gọi (β) là mặt phẳng chứa MN và song song với đường thẳng BC cắt đường thẳng SC tại P. Chứng minh rằng MP song song với mặt phẳng (SAB)
Câu 6 (1.0 điểm)
Hãy tìm số tự nhiên n khi biết 
. Trong đó là tổ hợp chập k phần tử của 2n phần tử.
Câu 7 (1.0 điểm)
Giải phương trình sau: 
Đáp án đề thi học kì 1 môn Toán lớp 11
