Đề thi Olympic Toán sinh viên ĐH Mỏ Địa Chất năm 2013

TRƯỜNG ĐẠI HỌC MỎ ĐỊA CHẤT ĐỀ CHÍNH THỨC

KỲ THI OLYMPIC TOÁN SINH VIÊN 2013 MÔN: TOÁN HỌC

MÔN: GIẢI TÍCH

Bài 1: (3 điểm)

Tính tích phân: .

Bài 2: (3 điểm):

Tính giới hạn sau: .

Bài 3: (3 điểm):

Tìm tất cả các giá trị của a thuộc R để hàm số: f(x) = |x - 1|. (a³x²2ax - 3) khả vi tại x = 1.

Bài 4: (4 điểm):

Cho hàm f(x) liên tục trên [0,1], khả vi trên (0,1) có f(1) = 0 chứng minh rằng tồn tại x_o thuộc (0; 1) để: f'(x_o).x_o1 = e^-f(xo).

Bài 5: (3 điểm):

Chứng minh hàm f(x) xác định trên R thỏa mãn: f(x1)f(x - 1) = √2.f(x) là một hàm tuần hoàn và tìm một chu kì của nó.

Bài 6: (4 điểm):

Cho f(x) là hàm chẵn, liên tục trên [-a; a], a thuộc R_*⁺, g(x) liên tục và nhận giá trị dương trên đoạn [-a, a] và
:

a. Chứng minh rằng: .

b. Tính:

MÔN: ĐẠI SỐ

Câu 1:

Cho a_o, d thuộc R và a_i = a_oid với . Hãy tính định thức sau: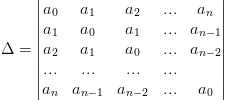

Câu 2:

Cho A, B là các ma trận vuông cấp n, (n ≥ 2), I là ma trận đơn vị cấp n. Giả sử AB2012A2013B = I. Chứng minh rằng: AB = BA.

Câu 3:

Cho X là ma trận cấp n không suy biến và có các cột là: X₁, X₂, ..., X_n (n ≥ 2). Cho Y là ma trận có các cột là X₂, X₃, ..., X_n, 0.

a) Tìm ma trận J thỏa mãn: Y = X.J

b) Chứng minh rằng các ma trận A = Y.X^-1; B = X^-1.Y chỉ có giá tri riêng là 0 và đều có hạng bằng n - 1.

Câu 4:

Cho ma trận A vuông cấp n có tất cả các phần tử bằng 1 hoặc -1. Chứng minh rằng: với n ≥ 3 thì |det(A)| ≤ (n - 1)(n - 1)!

Câu 5:

Tìm điều kiện của n nguyên dương để đa thức P(x) = xⁿ4 phân tích được thành tích của 2 đa thức có hệ số nguyên bậc nhỏ hơn n.

Câu 6:

Tìm tất cả các đa thức P(x) hệ số thực thỏa mãn: P(x²) - P²(x) = 2x[x - P(x)]