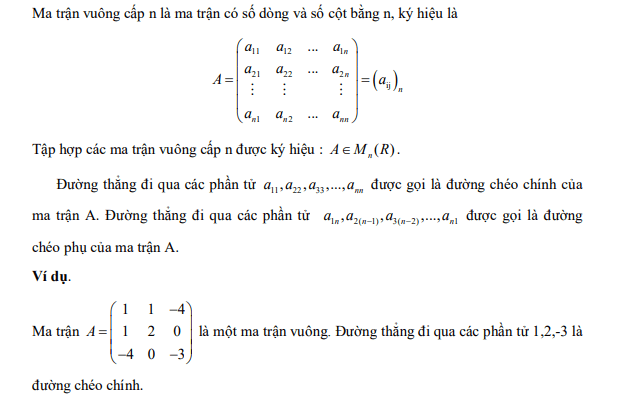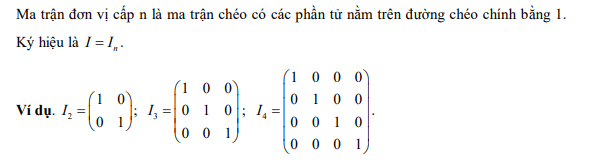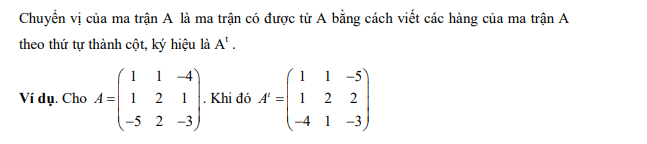Toán cao cấp là gì? Một số ví dụ về toán cao cấp Ma trận
Tìm hiểu về toán cao cấp
Thuật ngữ Toán cao cấp có vẻ còn xa lạ với nhiều bạn học sinh cấp 3. Tuy nhiên Toán cao cấp lại là một môn học quen thuộc đối với các bạn sinh viên học ngành kinh tế. Không những thế, ở các trường đại học, thì đây là môn mà hầu hết các ngành đều cần học và hiểu về nó. Mời bạn đọc cùng theo dõi bài viết dưới đây để hiểu rõ hơn về Toán cao cấp nhé.
1. Toán cao cấp là gì
Toán cao cấp chính là môn toán nhưng được giảng dạy với trình độ được nâng cao lên nhiều lần so với toán học phổ thông mà bạn đã được dạy. Toán cao cấp chỉ dành cho những đối tượng là sinh viên, cao đẳng đã đậu qua các kì thi tuyển sinh chính quy. Môn học này dựa trên những kiến thức căn bản của toán phổ thông, như là hình học không gian, lượng giác, xác xuất thông kê mà bạn đã được học trước đó, nhưng được nâng cấp lên một tâm cao khác, khó hơn. Chính vì thế mà nó được gọi là toán cao cấp.
Là một môn học khó, chính vì thế mà toán cao cấp đòi hỏi người học phải tập trung cao, chịu khó, chăm chỉ thì mới có thể giải được bài tập. Trong những trường Đại học và cao đẳng thì môn này thường được dạy cho những sinh viên ngành ngân hàng, kế toán, quản trị kinh doanh…
Để có thể đạt được kết quả tốt cho môn học này, ngoài chăm chỉ ra thì sinh viên còn cần có tu duy tốt. Ví dụ như chú ý nghe giảng, ghi chép đầy đủ cũng là các yếu tố quan trọng để có thể tiếp thu tốt môn này. Không những thế, để học tốt toán cao cấp, sinh viên cũng cần kiến thức về ma trận. Vậy toán cao cấp ma trận là gì? Có những dạng toán ma trận nào hay găp? Mời các bạn tiếp tục tìm hiểu bên dưới nhé!
2. Định nghĩa toán cao cấp ma trận là gì?
Ma trận A cấp m n trên R chính là một bảng số có hình chữ nhật bao gồm m hàng và n cột, sẽ được được biểu diễn như sau:
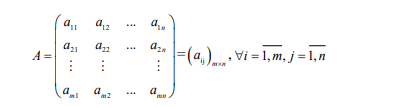
Trong đó:
3. Các dạng đặc biệt của ma trận
- Ma trận dòng
- Ma trận cột
- Ma trận không
- Ma trận vuông cấp n
- Ma trận tam giác
- Ma trận chéo
- Ma trận đơn vị cấp n
- Ma trận chuyển vị
- Ma trận đối xứng
4. Các phép toán trên ma trận
a. Phép cộng hai ma trận: (cùng cỡ)
Các tính chất: Giả sử A,B,C, θ là các ma trận cùng cấp, khi đó:
i) A + B = B + A
ii) A+ θ = A
iii) A + (B + C) = (A + B) + C
b. Phép nhân một số với một ma trận:
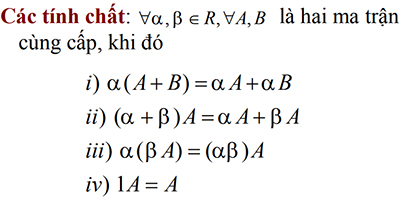c. Phép nhân hai ma trận:
Ma trận kết quả: Vị trí:
dòng 1, cột 1 = tổng (dòng 1 x cột 1)
dòng 1, cột 2 = tổng (dòng 1 x cột 2)
dòng 1, cột 3 = tổng (dòng 1 x cột 3)
....................................................
dòng i, cột j = tổng (dòng i x cột j)
....................................................
dòng m, cột n = tổng (dòng m x cột n)
Điều kiện nhân được của hai ma trận:
Là số phần tử trên dòng của ma trận A phải bằng số phần tử trên cột của ma trận B tương ứng.
Ví dụ về nhân ma trận:
Ví dụ: Cho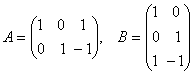 
, tính C = A.B
Ta có: c11 = 1.1 + 0.0 + 1.1 = 2
c12 = 1.0 + 0.1 + 1.(-1) = -1
c21 = 0.1 + 1.0 + (-).1 = -1
c22 = 0.0 + 1.1 + (-1).(-1) = 2 .
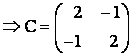
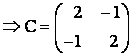
5. Các chủ đề chính của toán cao cấp
Toán cao cấp bao gồm nhiều chủ đề khác nhau, mỗi chủ đề đều có ý nghĩa và ứng dụng riêng. Dưới đây là những chủ đề chính của toán cao cấp:
Giải tích
Giải tích là một trong những chủ đề quan trọng nhất của toán cao cấp. Nó nghiên cứu về giới hạn, tích phân, chuỗi, phương trình vi phân, và các khái niệm khác. Giải tích có nhiều ứng dụng trong các lĩnh vực như vật lý, kinh tế, và khoa học máy tính.
Đại số tuyến tính
Đại số tuyến tính là một chủ đề quan trọng của toán cao cấp, nghiên cứu về các đại số học liên quan đến các hàm tuyến tính, ma trận và hệ phương trình tuyến tính. Đại số tuyến tính được sử dụng trong nhiều lĩnh vực như kỹ thuật, khoa học máy tính và kinh tế.
Xác suất thống kê
Xác suất thống kê là một chủ đề quan trọng của toán cao cấp, nghiên cứu về xác suất, phân phối xác suất và các phương pháp thống kê. Xác suất thống kê được sử dụng trong nhiều lĩnh vực như tài chính, y tế và khoa học dữ liệu.
Giải tích số
Giải tích số là một chủ đề quan trọng của toán cao cấp, nghiên cứu về phương pháp tính toán số, ước lượng và giải phương trình số. Giải tích số được sử dụng trong nhiều lĩnh vực như khoa học máy tính, kỹ thuật và vật lý.
Hình học
Hình học là một chủ đề quan trọng của toán cao cấp, nghiên cứu về các đối tượng hình học như không gian, hình khối và các đường cong. Hình học được sử dụng trong nhiều lĩnh vực như kiến trúc, đồ họa và khoa học vật liệu.
Tóm lại, toán cao cấp bao gồm nhiều chủ đề khác nhau, mỗi chủ đề đều có ý nghĩa và ứng dụng riêng, giúp chúng ta hiểu rõ hơn về các quá trình xảy ra xung quanh chúng ta.
.........................
Trên đây, VnDoc đã giới thiệu tới các bạn tài liệu Toán cao cấp là gì? Một số ví dụ về toán cao cấp Ma trận. Bài viết cho chúng ta thấy được khái niệm về Toán cao cấp, định nghĩa toán cao cấp ma trận, một số ví dụ về toán cap cấp ma trận... Mời bạn đọc cùng tham khảo thêm tại mục Cao đẳng, Đại học để có thêm nhiều tài liệu học tập nhé.
Mời các bạn tham khảo thêm tài liệu học tập:
