Bài tập xác suất thống kê
Bài tập xác suất thống kê có đáp án kèm theo
Bài tập xác suất thống kê gồm bài tập về xác suất thống kê có lời giải, giúp các bạn sinh viên củng cố các kiến thức được học của môn Xác suất thống kê. Từ đó, giúp các bạn có kế hoạch học tập và ôn thi môn xác suất thống kê hiệu quả hơn. Mời các bạn cùng tham khảo các bài tập môn xác suất thống kê dưới đây.
Xác suất thống kê
Bài Tập Xác Suất Thống Kê
Bài 1: Có 30 đề thi trong đó có 10 đề khó, 20 đề trung bình. Tìm xác suất để:
a. Một học sinh bắt một đề gặp được đề trung bình.
b. Một học sinh bắt hai đề, được ít nhất một đề trung bình.
Giải
a. Gọi A là biến cố học sinh bắt được đề trung bình:
![]()
b. Gọi B là biến cố học sinh bắt được 1 đề trung bình và một đề khó
Gọi C là biến cố học sinh bắt được 2 đề trung bình.
Gọi D là biến cố học sinh bắt hai đề, được ít nhất một đề trung bình.
Khi đó:
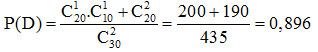
Bài 2: Có hai lớp 10A và 10 B mỗi lớp có 45 học sinh, số học sinh giỏi văn và số học sinh giỏi toán được cho trong bảng sau. Có một đoàn thanh tra. Hiệu trưởng nên mời vào lớp nào để khả năng gặp được một em giỏi ít nhất một môn là cao nhất?
|
Lớp Giỏi |
10A |
10B |
|
Văn |
25 |
25 |
|
Toán |
30 |
30 |
|
Văn và Toán |
20 |
10 |
Giải
Gọi V là biến cố học sinh giỏi Văn, T là biến cố học sinh giỏi Toán.
Ta có: Lớp 10A
P(V + T) = P(V) + P(T) - P(VT) = 25/45 + 30/45 - 20/45 = 7/9
Lớp 10B:
P(V + T) = P(V) + P(T) - P(VT) = 25/45 + 30/45 - 10/45 = 1
Vậy nên chọn lớp 10B.
Bài 3: Lớp có 100 sinh viên, trong đó có 50 SV giỏi Anh Văn, 45 SV giỏi Pháp Văn, 10 SV giỏi cả hai ngoại ngữ. Chọn ngẫu nhiên một sinh viên trong lớp. Tính xác suất:
a. Sinh viên này giỏi ít nhất một ngoại ngữ.
b. Sinh viên này không giỏi ngoại ngữ nào hết.
c. Sinh viên này chỉ giỏi đúng một ngoại ngữ.
d. Sinh viên này chỉ giỏi duy nhất môn Anh Văn.
Giải
a) Gọi A là biến cố Sinh viên giỏi Anh Văn.
Gọi B là biến cố Sinh viên giỏi Pháp Văn.
Gọi C là biến cố Sinh viên giỏi ít nhất một ngoại ngữ.
P(C) = P(A + B) = P(A) + P(B) - P(AB) = 50/100 + 45/100 - 10/100 = 0,85
b) Gọi D là biến cố Sinh viên này không giỏi ngoại ngữ nào hết.
P(D) = 1 - P(C) = 1 - 0,85 = 0,15