Đề thi thử THPT Quốc gia môn Toán năm 2016 trường THPT Thủ Đức, TP. Hồ Chí Minh
Đề thi thử THPT Quốc gia môn Toán năm 2016
Đề thi thử THPT Quốc gia môn Toán năm 2016 trường THPT Thủ Đức, TP. Hồ Chí Minh có đáp án đi kèm, là tài liệu luyện tập hữu ích dành cho các bạn học sinh, giúp các bạn củng cố và nâng cao kỹ năng làm bài môn Toán, từ đó, chuẩn bị tốt nhất cho kì thi THPT Quốc gia, luyện thi Đại học, Cao đẳng 2016 hiệu quả.
Đề thi thử THPT Quốc gia môn Toán năm 2016 trường THPT Phùng Khắc Khoan, Hà Nội
Đề thi thử THPT Quốc gia năm 2016 môn Toán trường THPT Tam Dương, Vĩnh Phúc (Lần 4)
Đề thi thử THPT Quốc gia năm 2016 môn Toán trường THPT Chuyên Võ Nguyên Giáp, Quảng Bình
|
TRƯỜNG THPT THỦ ĐỨC NĂM HỌC 2015-2016 |
ĐỀ THI THỬ THPT QUỐC GIA - MÔN THI: TOÁN Thời gian làm bài: 180 phút, không kể thời gian phát đề |
Câu 1 (2,0 điểm).
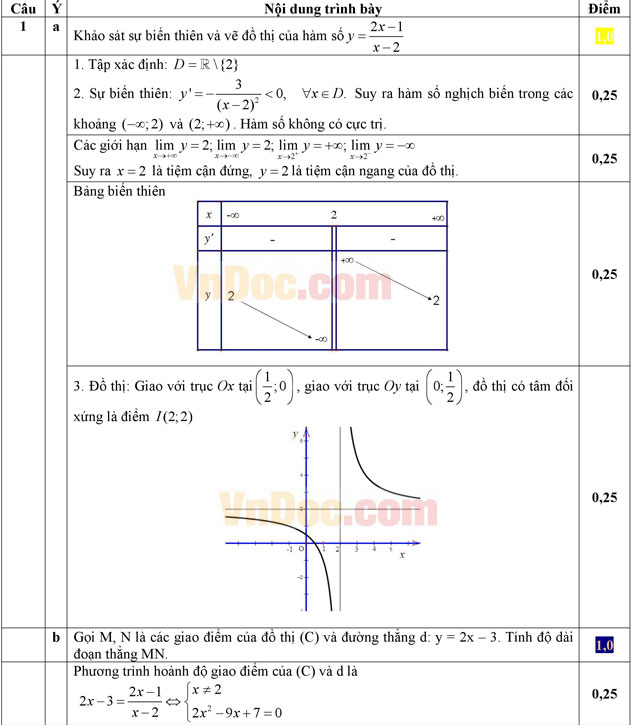
a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số 
.
b) Gọi M, N là các giao điểm của đồ thị (C) và đường thẳng d: y = 2x – 3. Tính độ dài đoạn thẳng MN.
Câu 2 (1,0 điểm).
a) Giải phương trình 
(x ∈ R)
b) Trong mặt phẳng 0xy, tìm tọa độ điểm M biểu diễn số phức z thỏa mãn z(2i - 1) - i + 2 = 0.
Câu 3 (1,0 điểm). Tính tích phân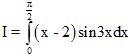 
.
Câu 4 (1,0 điểm). Trong không gian với hệ trục tọa độ Oxyz, cho điểm A(2; –5; –6) và đường thẳng 
. Tìm tọa độ hình chiếu vuông góc của A trên (Δ). Viết phương trình đường thẳng đi qua A và cắt (Δ) tại B sao cho AB = √35.
Câu 5 (1,0 điểm).
a) Cho góc α thỏa mãn 
. Tính giá trị biểu thức A = sin2α + cos2α.
b) Giải bóng đá công đoàn các trường THPT trong cụm 8 quy tụ 10 đội bóng đá nam gồm: Nguyễn Hữu Huân, Thủ Đức, Đào Sơn Tây, Hiệp Bình, Tam Phú, Nguyễn Huệ, Phước Long, Long Trường, Nguyễn Văn Tăng và Ngô Thời Nhiệm. Các đội được chia thành hai bảng A và B, mỗi bảng 5 đội. Việc chia bảng được thực hiện bằng cách bốc thăm ngẫu nhiên. Tính xác suất để hai đội Thủ Đức và Nguyễn Hữu Huân nằm ở hai bảng khác nhau.
Câu 6 (1,0 điểm). Cho hình chóp S.ABC có SA ⊥ (ABC) và ABC là tam giác đều cạnh 2a. Cạnh bên SB = 3a. Gọi M là trung điểm cạnh SC. Tính thể tích khối chóp S.ABC và khoảng cách giữa hai đường thẳng AC và BM theo a.
Câu 7 (1,0 điểm). Trong mặt phẳng tọa độ Oxy cho tam giác ABC, có M(3; -1) là trung điểm cạnh BC. Đường thẳng chứa đường cao đỉnh B đi qua E(-1; -3). Đường thẳng chứa cạnh AC đi qua F(1; 3). Tìm tọa độ các đỉnh của tam giác ABC, biết đường tròn ngoại tiếp tam giác ABC có đường kính AD với D(4; -2).
Câu 8 (1,0 điểm). Giải hệ phương trình: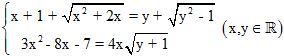 
.
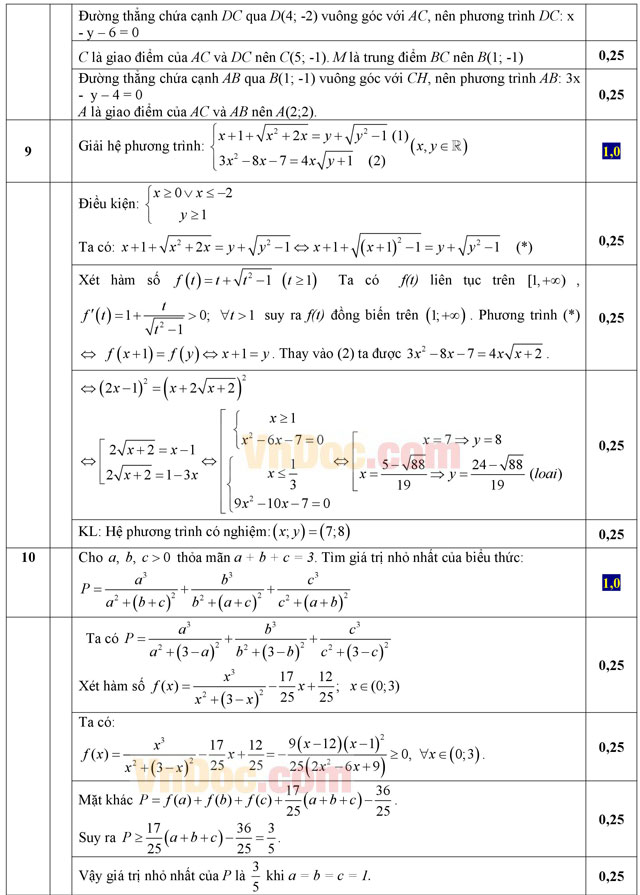
Câu 9 (1,0 điểm). Cho a, b, c > 0 thỏa mãn a + b + c = 3. Tìm giá trị nhỏ nhất của biểu thức:
Đáp án đề thi thử THPT Quốc gia môn Toán năm 2016
