Đề thi thử THPT Quốc gia môn Toán năm 2016 trường THPT Phùng Khắc Khoan, Hà Nội

Đề thi thử THPT Quốc gia môn Toán năm 2016

Đề thi thử THPT Quốc gia môn Toán năm 2016 trường THPT Phùng Khắc Khoan, Hà Nội gồm 10 câu hỏi cùng đáp án đi kèm, được làm trong thời gian 180 phút. Đây là tài liệu ôn tập hữu ích dành cho các bạn học sinh lớp 12, những bạn chuẩn bị bước vào kì thi THPT Quốc gia sắp tới. Mời các bạn tham khảo.

Đề thi thử THPT Quốc gia năm 2016 môn Toán trường THPT Chuyên Khoa học Tự nhiên, Hà Nội (Lần 3)

Đề thi thử THPT Quốc gia môn Toán năm 2016 Sở GD-ĐT Hà Nội

SỞ GIÁO DỤC & ĐÀO TẠO HÀ NỘI TRƯỜNG THPT PHÙNG KHẮC KHOAN - THẠCH THẤT -

ĐỀ THI THỬ KỲ THI THPT QUỐC GIA NĂM 2016 Môn: TOÁN - Ngày thi: 16 / 05 / 2016 Thời gian làm bài: 180 phút, không kể thời gian phát đề

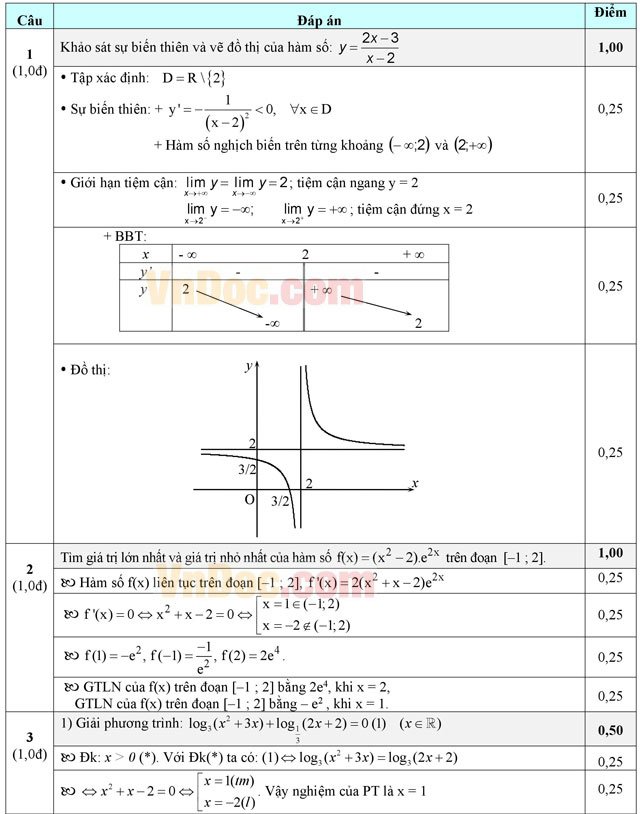
Câu 1 (1,0 điểm). Khảo sát sự biến thiên và vẽ đồ thị của hàm số

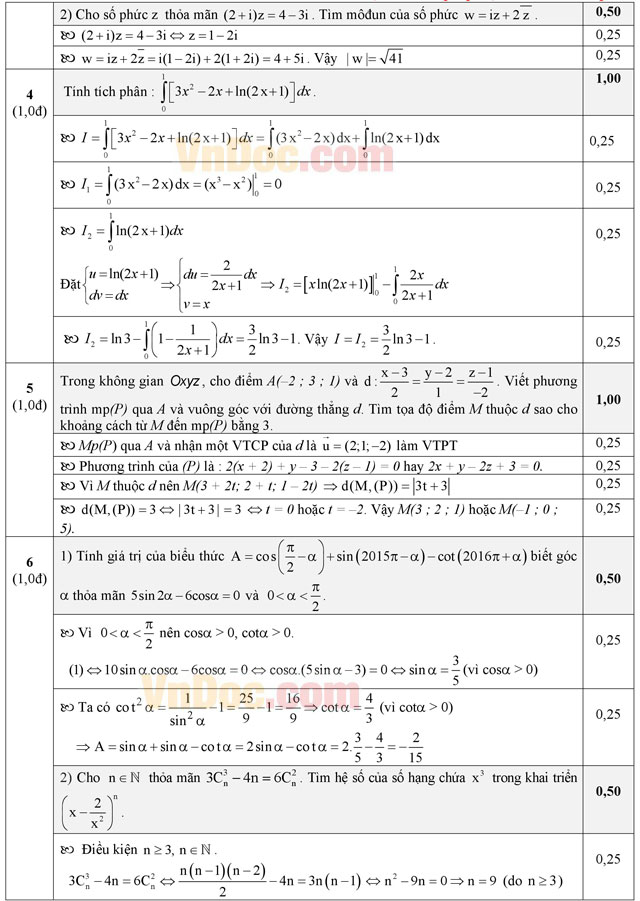
Câu 2 (1,0 điểm). Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số f(x) = (x² - 2).e^2x trên đoạn [–1; 2].

Câu 3 (1,0 điểm).

1. Giải phương trình
2. Cho số phức z thỏa mãn (2 + i)z = 4 - 3i. Tìm môđun của số phức .

Câu 4 (1,0 điểm). Tính tích phân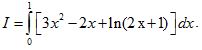

Câu 5 (1,0 điểm). Trong không gian với hệ tọa độ Oxy, cho điểm A(–2; 3; 1) và đường thẳng . Viết phương trình mặt phẳng (P) qua A và vuông góc với đường thẳng d. Tìm tọa độ điểm M thuộc đường thẳng d sao cho khoảng cách từ M đến mặt phẳng (P) bằng 3.

Câu 6 (1,0 điểm).

1. Tính giá trị của biểu thức biết góc α thỏa mãn 5sin2α - 6cosα = 0 và 0 < α < π/2.
2. Cho n là số tự nhiên thỏa mãn . Tìm hệ số của số hạng chứa x³ trong khai triển .

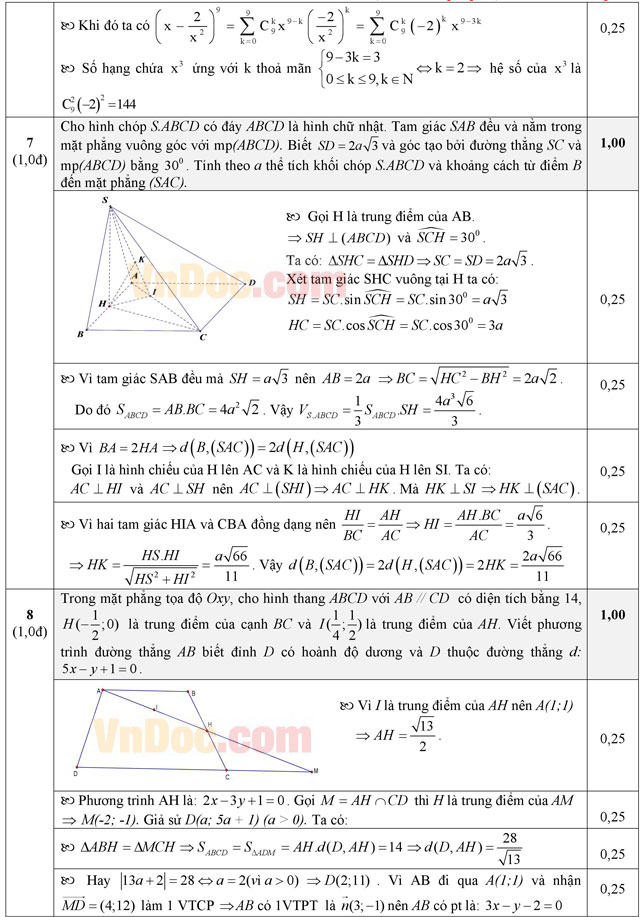
Câu 7 (1,0 điểm). Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật. Tam giác SAB đều và nằm trong mặt phẳng vuông góc với mặt phẳng (ABCD). Biết SD = 2a√3 và góc tạo bởi đường thẳng SC và mặt phẳng (ABCD) bằng 30^o. Tính theo a thể tích khối chóp S.ABCD và khoảng cách từ điểm B đến mặt phẳng (SAC).

Câu 8 (1,0 điểm). Trong mặt phẳng với hệ tọa độ Oxy, cho hình thang ABCD với AB // CD có diện tích bằng 14, H(-1/2; 0) là trung điểm của cạnh BC và I(1/4; 1/2) là trung điểm của AH. Viết phương trình đường thẳng AB biết đỉnh D có hoành độ dương và D thuộc đường thẳng d: 5x - y + 1 = 0.

Câu 9 (1,0 điểm). Giải hệ phương trình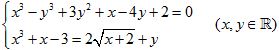

Câu 10 (1,0 điểm). Cho các số thực dương a, b, c. Tìm giá trị nhỏ nhất của biểu thức

Đáp án đề thi thử THPT Quốc gia môn Toán năm 2016