Đề thi thử THPT Quốc gia môn Toán năm 2016 trường THPT Trực Ninh, Nam Định (Lần 1)
Đề thi thử THPT Quốc gia môn Toán năm 2016
Đề thi thử THPT Quốc gia môn Toán năm 2016 trường THPT Trực Ninh, Nam Định (Lần 1) là đề thi thử đại học môn Toán có đáp án đi kèm. Đây sẽ là tài liệu hữu ích dành cho các bạn nghiên cứu, tham khảo. Hy vọng các bạn sẽ đạt điểm cao trong kỳ thi sắp tới.
Đề thi thử THPT Quốc gia môn Toán năm 2016 trường THPT Đông Sơn 1, Thanh Hóa (Lần 3)
Đề thi thử THPT Quốc gia năm 2016 môn Toán trường THPT Chuyên Vĩnh Phúc (Lần 5)
Đề thi thử THPT Quốc gia môn Toán năm 2016 trường THPT Chu Văn An, Hà Nội
| SỞ GIÁO DỤC VÀ ĐÀO TẠO NAM ĐỊNH TRƯỜNG THPT TRỰC NINH ĐỀ CHÍNH THỨC |
KỲ THI THỬ THPT QUỐC GIA LẦN 1 NĂM 2016 Môn thi: TOÁN Thời gian: 180 phút, không kể thời gian phát đề |
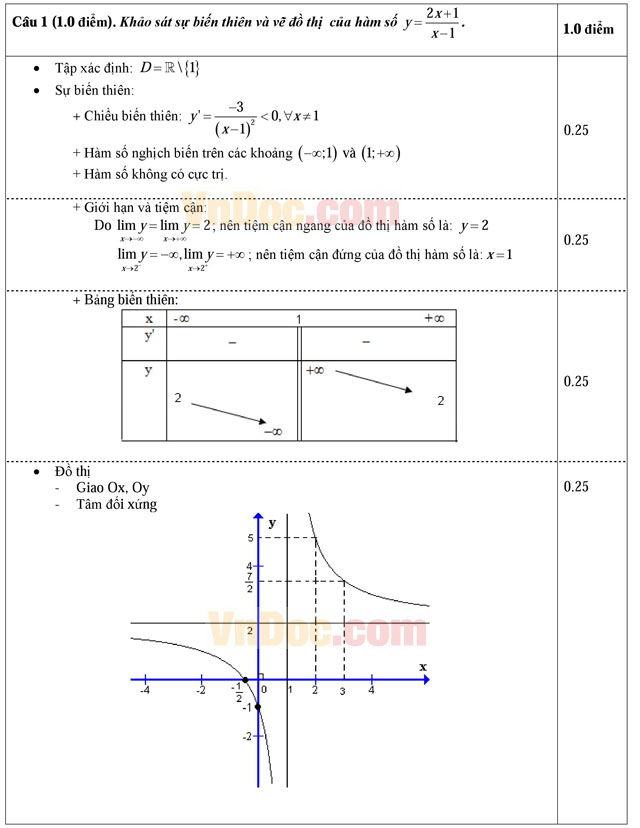
Câu 1 (1.0 điểm). Khảo sát sự biến thiên và vẽ đồ thị của hàm số ![]()
Câu 2 (1.0 điểm).
a) Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số f(x) = x2 - ln(1 - 2x) trên đoạn [-2; 0].
b) Tìm m để hàm số y = x3 - 3(m + 1)x2 + 9x - 2016m đạt cực tiểu tại điểm x = 3.
Câu 3 (1.5 điểm). Giải phương trình:
a) log3(x + 2) + log3(x + 4) - log√3(8 - x) = 1.
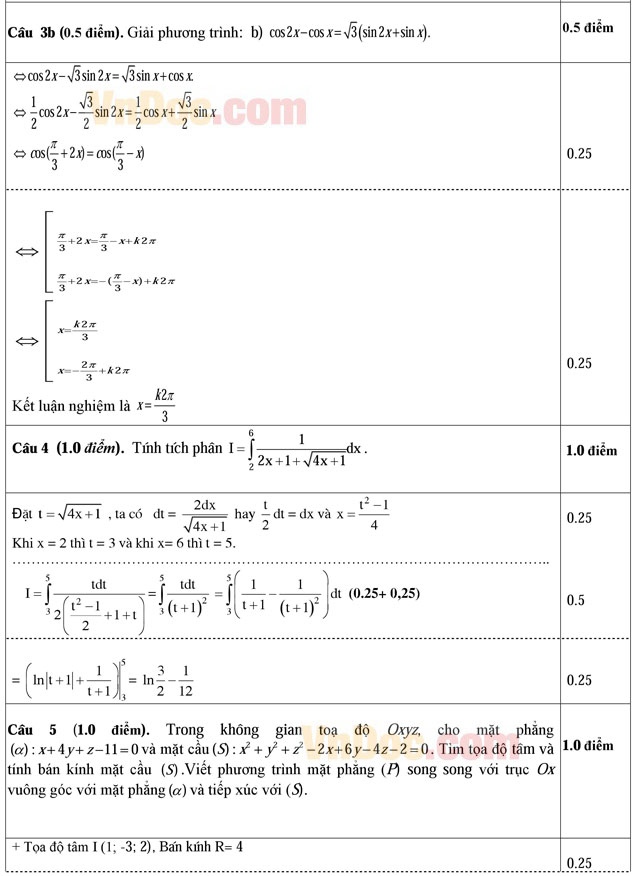
b) cos2x - cosx = √3(sin2x + sinx)
Câu 4 (1.0 điểm). Tính tích phân 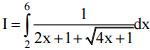 .
.
Câu 5 (1.0 điểm). Trong không gian toạ độ Oxyz, cho mặt phẳng (α): x + 4y + z - 11 = 0 và mặt cầu (S): x2 + y2 + z2 - 2x + 6y - 4z - 2 = 0. Tìm tọa độ tâm và tính bán kính mặt cầu (S). Viết phương trình mặt phẳng (P) song song với trục Ox vuông góc với mặt phẳng (α) và tiếp xúc với mặt cầu (S).
Câu 6 (0.5 điểm). Một bộ đề thi toán học sinh giỏi lớp 12 mà mỗi đề thi gồm 5 câu được chọn từ 15 câu dễ, 10 câu trung bình và 5 câu khó. Một đề thi được gọi là "Tốt" nếu trong đề thi đó có ba loại câu dễ, trung bình và khó, đồng thời số câu dễ không ít hơn 2. Lấy ngẫu nhiên một đề trong bộ đề trên. Tính xác suất để đề thi lấy ra là một đề thi "Tốt".
Câu 7 (1.0 điểm). Cho hình lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác đều cạnh a. Góc giữa CA' và mặt phẳng (AA'B'B)
bằng 30o. Tính theo a thể tích khối lăng trụ ABC.A'B'C' và khoảng cách giữa AI' và AC với I là trung điểm AB.
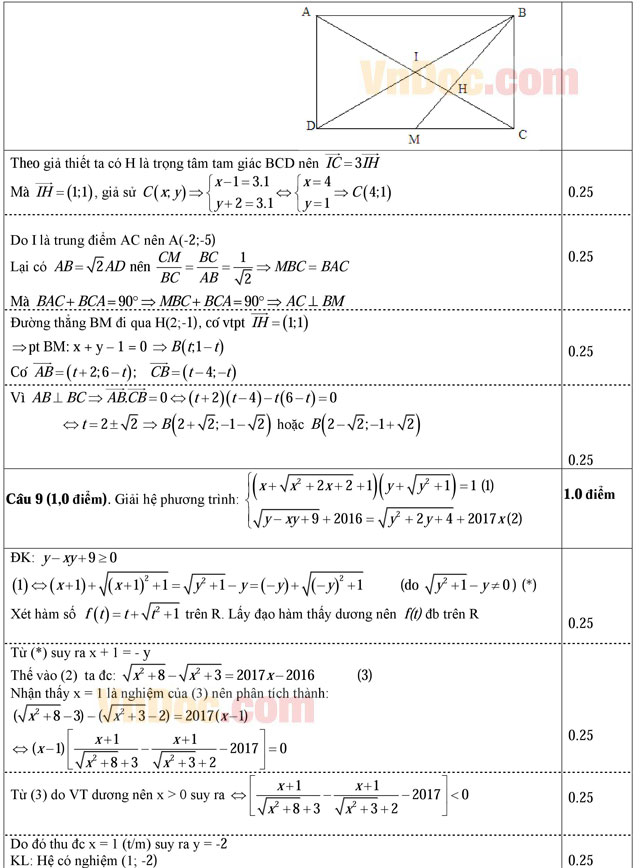
Câu 8 (1.0 điểm). Trong mặt phẳng tọa độ Oxy, cho hình chữ nhật ABCD có AB = AD√2, tâm I(1; -2). Gọi M là trung điểm cạnh CD, H(2; -1) là giao điểm của hai đường thẳng AC và BM. Tìm tọa độ các điểm A, B.
Câu 9 (1.0 điểm). Giải hệ phương trình 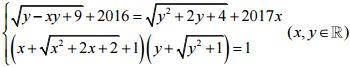
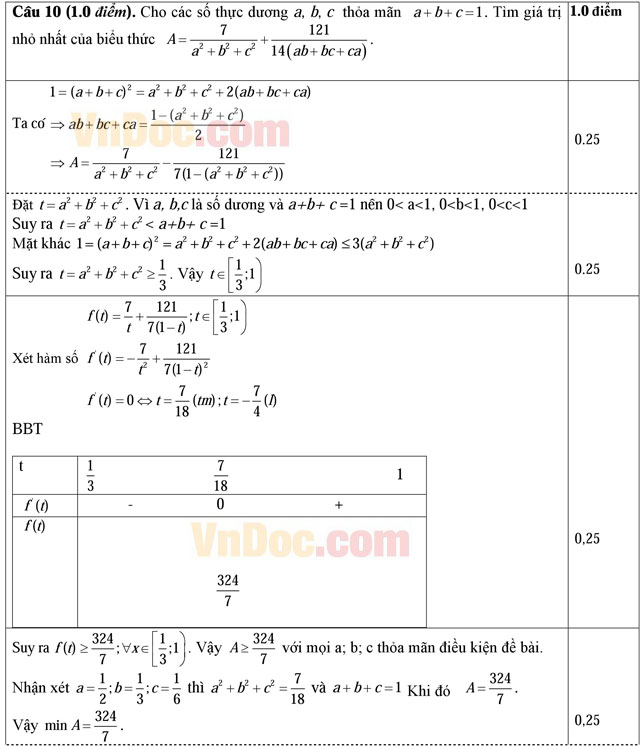
Câu 10 (1.0 điểm). Cho các số thực dương a, b, c thỏa mãn a + b + c = 1. Tìm giá trị nhỏ nhất của biểu thức ![]()
Đáp án đề thi thử THPT Quốc gia môn Toán năm 2016