Đề thi tổng diễn tập THPT Quốc gia môn Toán năm 2016 trường THPT Chuyên Nguyễn Quang Diêu, Đồng Tháp

Đề thi thử THPT Quốc gia môn Toán năm 2016

Đề thi tổng diễn tập THPT Quốc gia môn Toán năm 2016 trường THPT Chuyên Nguyễn Quang Diêu, Đồng Tháp là đề thi thử đại học môn Toán có chất lượng, bao gồm đề thi và đáp án. Hi vọng bộ tài liệu này giúp các bạn ôn thi THPT Quốc gia, ôn thi đại học có hiệu quả.

Phương pháp giải bất phương trình vô tỷ chứa căn (Có lời giải)

Đề thi thử THPT Quốc gia năm 2016 môn Toán trường THPT Chuyên Đại học Sư phạm Hà Nội (Lần 2)

Đề thi tổng diễn tập THPT Quốc gia môn Ngữ văn năm 2016 trường THPT Chuyên Nguyễn Quang Diêu, Đồng Tháp

SỞ GDĐT ĐỒNG THÁP TRƯỜNG THPT CHUYÊN NGUYỄN QUANG DIÊU

ĐỀ THI DIỄN TẬP THPT QUỐC GIA NĂM 2016 MÔN: TOÁN Thời gian làm bài: 180 phút (Không kể thời gian giao đề) Ngày Thi: 17/06/2016

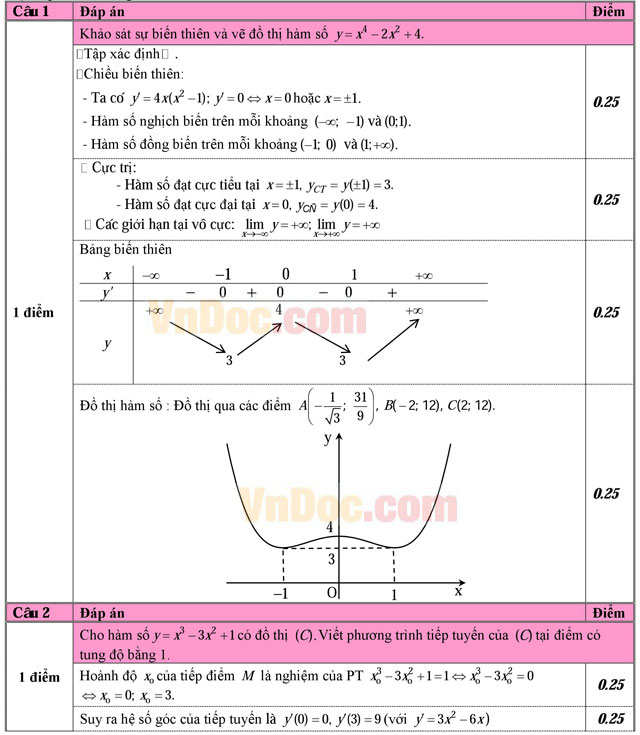
Câu 1 (1,0 điểm). Khảo sát sự biến thiên và vẽ đồ thị hàm số y = x⁴ - 2x² + 4

Câu 2 (1,0 điểm). Cho hàm số y = x³ - 3x² + 1 có đồ thị (C). Viết phương trình tiếp tuyến của (C) tại điểm có tung độ bằng 1.

Câu 3 (1,0 điểm).

a) Cho số phức z thỏa mãn điều kiện Tìm môđun của số phức .

b) Giải phương trình 27^x - 5.3^2-3x = 4.

Câu 4 (1,0 điểm). Tính tích phân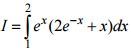

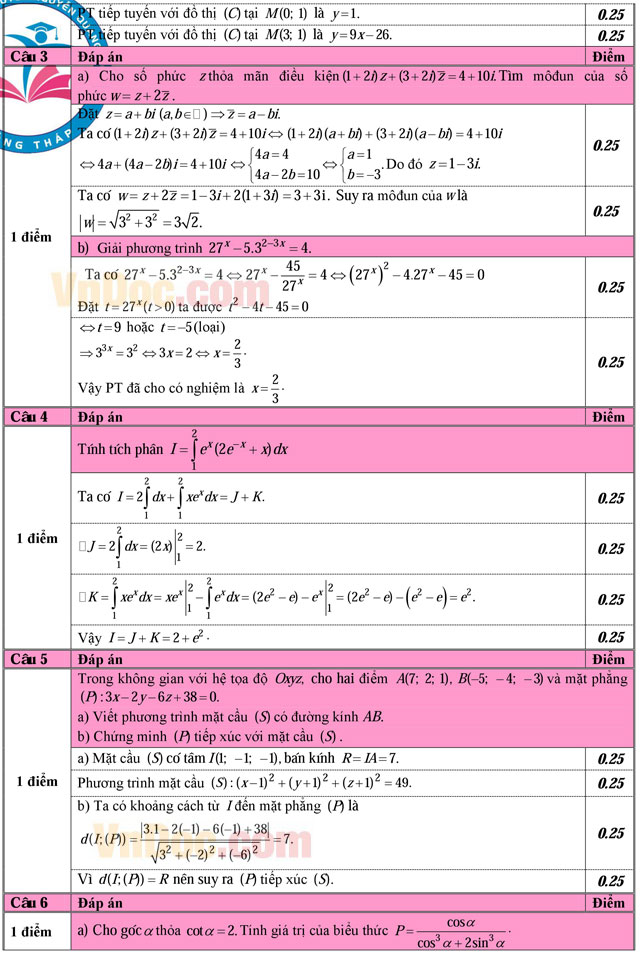
Câu 5 (1,0 điểm). Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(7; 2; 1), B(-5; -4; -3) và mặt phẳng (P): 3x - 2y - 6z + 38 = 0.

a) Viết phương trình mặt cầu (S) có đường kính AB.

b) Chứng minh (P) tiếp xúc với mặt cầu (S).

Câu 6 (1,0 điểm).

a) Cho góc α thỏa cotα = 2. Tính giá trị của biểu thức

b) Tìm hệ số của số hạng chứa x⁷ trong khai triển

Câu 7 (1,0 điểm). Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a; BCD = 60^o; SA vuông góc với mặt phẳng (ABCD), hai mặt phẳng (SCB) và (SCD) vuông góc với nhau. Tính thể tích khối chóp S.ABCD và khoảng cách từ C đến mặt phẳng (SBD) theo a.

Câu 8 (1,0 điểm). Trong mặt phẳng với hệ tọa độ Oxy, cho hình chữ nhật ABCD, A(2; 2), BC = 3BA, trọng tâm của tam giác ABC là G(0; 10/3). Tìm tọa độ các đỉnh còn lại của hình chữ nhật ABCD biết rằng đỉnh B có hoành độ dương, đường trung tuyến kẻ từ B của tam giác ABD có hệ số góc nhỏ hơn 1.

Câu 9 (1,0 điểm). Tìm m để hệ sau có hai nghiệm phân biệt: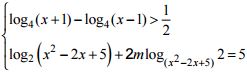

Câu 10 (1,0 điểm). Cho x, y, z là các số thực dương thỏa mãn x² + y² + 2z² ≥ 2(1 - xy). Tìm giá trị nhỏ nhất của biểu thức

Đáp án đề thi thử THPT Quốc gia môn Toán năm 2016