Đề thi thử vào lớp 10 môn Toán sở GD&ĐT Yên Lãng, Hải Phòng năm 2014 - 2015

Đề thi thử vào lớp 10 môn Toán

Đề thi thử vào lớp 10 môn Toán sở GD&ĐT Yên Lãng, Hải Phòng năm 2014 - 2015 được VnDoc.com sưu tầm và giới thiệu tới các bạn học sinh nhằm giúp các em học sinh có thêm nhiều tài liệu ôn thi vào lớp 10 môn Toán hiệu quả. Mời các em cùng tham khảo.

Đề thi thử vào lớp 10 môn Toán trường THCS Văn Khuê năm 2014 - 2015

Đề thi thử vào lớp 10 môn Ngữ văn trường THPT Chuyên quốc học Huế, Thừa Thiên Huế năm 2014 - 2015

I) TRẮC NGHIỆM: (2,0 điểm). Ghi lại chỉ một chữ cái đứng trước đáp án đúng

Câu 1. Điều kiện để biểu thức √(4x -3) có nghĩa là:

Câu 2. Trong mặt phẳng tọa độ Oxy, đường thẳng y = 5x + m (d) đi qua điểm M(1; –2), thì m =?:

A. –7; B. 11; C. –3; D. 3;

Câu 3. Phương trình nào sau đây có nghiệm kép?

A. x² – x = 0; B. 3x² + 2 = 0; C. 3x² + 2x + 1 = 0; D. 9x² + 12x + 4 = 0;

Câu 4. Hai số –5 và 3 là nghiệm của phương trình nào sau đây?

A. x² + 2x + 15 = 0; B.x² – 2x – 15 = 0;

C. x² + 2x – 15 = 0; D. x² – 8x + 15 = 0;

Câu 5. Trong DABC vuông tại A, AH là đường cao, AB = 8cm; BH = 4cm. Độ dài cạnh BC =?

A. 24cm; B. 32cm; C. 18cm; D. 16cm;

Câu 6. Trong DABC có góc BAC bằng 70^o, góc ABC bằng 60^o, nội tiếp đường tròn (O), số đo của góc AOB bằng

A. 50^o; B. 100^o; C. 120^o; D. 14^0o;

Câu 7. Trong DABC vuông tại A, có BC = a, góc ABC bằng 30^o, độ dài cạnh AB bằng

Câu 8. Một hình trụ có chiều cao bằng hai lần đường kính đáy, nếu đường kính đáy bằng 4 cm thì thể tích hình trụ bằng?

A. 16π cm³; B. 32π cm³; C. 64π cm³; D. 128π cm³;

II) TỰ LUẬN: (8,0 điểm)

Câu 1. (1,5 điểm)

1) Rút gọn các biểu thức sau:

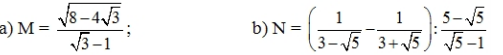
2) Cho Parabol y = x² (P) và đường thẳng y = 2x – m (d). Tìm các giá trị của m sao cho (P) và (d) cắt nhau tại hai điểm phân biệt.

Câu 2. (2,0 điểm)

1) Cho hệ phương trình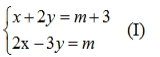

a) Giải hệ (I) khi m = 1.

b) Tìm m để hệ (I) có nghiệm duy nhất (x; y) thỏa mãn x + y = – 3

2) Cho phương trình x² + 2x – m = 0 (1) (x là ẩn, m là tham số)

a) Giải phương trình với m = –1

b) Tìm tất cả các giá trị của m để phương trình (1) có nghiệm. Gọi x₁, x₂ là hai nghiệm (có thể bằng nhau) của phương trình (1). Tìm giá trị nhỏ nhất của biểu thức P = x¹⁴ + x²⁴ theo m.

Câu 3. (3,5 điểm). Cho điểm M nằm ngoài đường tròn (O), Vẽ các tiếp tuyến MA, MB (A, B là các tiếp điểm), và cát tuyến MCD không đi qua O (C nằm giữa M và D) với đường tròn (O).

1) Chứng minh tứ giác MAOB nội tiếp

2) Chứng minh MC.MD = MA2.

3) Đường thẳng MO cắt AB tại H và cắt (O) tại I, K (I nằm giữa M và K). Chứng minh

4) Chứng minh CK là phân giác của góc DCH.

Câu 4. (1,0 điểm). Cho a, b, c > 0. Chứng minh:

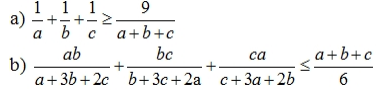
Đáp án đề thi thử vào lớp 10 môn Toán