Đề thi tuyển sinh vào lớp 10 môn Toán sở GD&ĐT Tiền Giang năm 2015 - 2016

Đề thi tuyển sinh vào lớp 10 môn Toán

Đề thi tuyển sinh vào lớp 10 môn Toán sở GD&ĐT Tiền Giang năm 2015 - 2016 được VnDoc sưu tầm và đăng tải nhằm giúp các em học sinh có thêm nhiều tài liệu ôn thi vào lớp 10 môn Toán để tham khảo chuẩn bị tốt cho kì thi tuyển sinh sắp tới đây đạt kết quả cao. Mời các em cùng tham khảo.

Đề thi tuyển sinh vào lớp 10 môn Ngữ văn năm học 2015-2016 Sở GD-ĐT Bình Định

Đề thi tuyển sinh vào lớp 10 môn Ngữ văn năm học 2015-2016 Sở GD-ĐT Phú Thọ

Bài I: (2,5 điểm)

1. Rút gọn biểu thức sau:

2. Giải hệ phương trình và các phương trình sau:

b/ x² - 2x - 8 = 0 c/ x⁴ - 3x² - 4 = 0

Bài II: (1,0 điểm)

Cho phương trình x² - 2(m - 1)x + m² - 3m = 0 (x là ẩn số, m là tham số)

1. Định m để phương trình có hai nghiệm x₁, x₂.

2. Tìm giá trị nhỏ nhất của biểu thức B = x₁² + x₂² + 7

Bài III: (2,0 điểm)

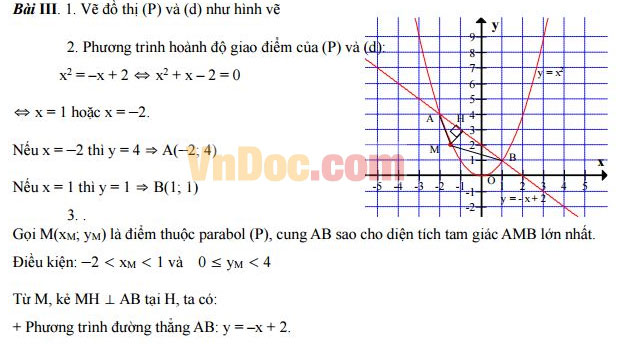
Cho parabol (P) : y = x² và đường thẳng (d) : y = -x + 2

1. Vẽ đồ thị của (P) và (d) trên cùng mặt phẳng tọa độ.

2. Bằng phép tính, xác định tọa độ các giao điểm A, B của (P) và (d).

3. Tìm tọa độ điểm M trên cung AB của đồ thị (P) sao cho tam giác AMB có diện tích lớn nhất.

Bài IV: (1,5 điểm) Khoảng cách giữa hai bến sông A và B là 30 km. Một canô đi xuôi dòng từ A đến B, rối đi ngược dòng trở về A ngay. Thời gian kể từ lúc đi cho đến lúc về là 5 giờ 20 phút. Tính vận tốc của dòng nước, biết vận tốc thực của canô là 12 km/h

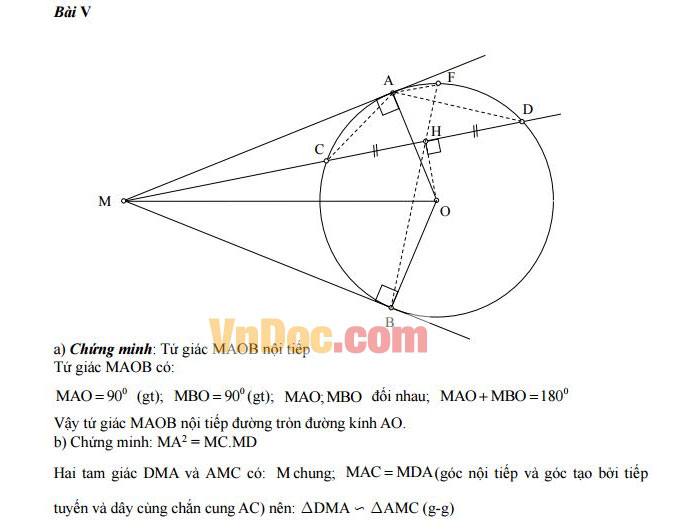
Bài V (2,0 điểm) Cho đường tròn tâm O. Từ điểm M nằm ngoài đường tròn (O) vẽ các tiếp tuyến MA, MB với (O) (A, B là hai tiếp điểm). Vẽ cát tuyến MCD không đi qua tâm O, C nằm giữa M và D.

1. Chứng minh: Tứ giác MAOB nội tiếp trong một đường tròn.

2. Chứng minh: MA² = MC.MD.

3. Gọi trung điểm của dây CD là H, tia BH cắt O tại điểm F. Chứng minh: AF // CD

Bài 6 (1,0 điểm) Cho một hình nón có bán kính đáy bằng 5 cm, đường sinh bằng 13 cm. Tính diện tích xung quanh và thể tích của hình nón đã cho

Đáp án đề thi tuyển sinh vào lớp 10 môn Toán