Giải Toán 8 trang 100 tập 2 Kết nối tri thức
Giải Toán 8 trang 100 Tập 2
Giải Toán 8 trang 100 Tập 2 Kết nối tri thức hướng dẫn giải chi tiết cho các câu hỏi và bài tập trong SGK Toán 8 Kết nối tri thức tập 2 trang 100.
Thử thách nhỏ trang 100 Toán 8 tập 2 Kết nối
Một người đo chiều cao của một cái cây bằng cách cắm một chiếc cọc xuống đất, cọc cao 2,4m và cách vị trí gốc cây 19m. Người đo đứng cách xa chiếc cọc 1m và nhìn thấy đỉnh cọc thẳng với đỉnh của cây. Hãy tính chiều cao của cây, biết rằng khoảng cách từ chấn đến mắt người ấy là 1,6m(H9.51).
Hướng dẫn giải:
Hai tam giác vuông CMX (vuông tại X) và AMY (vuông tại Y) có chung góc nhọn là góc M
Do đó ∆ABC ∽ ∆XZY
Suy ra 
\(\frac{CX}{AY}=\frac{MX}{MY}\) hay \(AY=\frac{CX.MY}{MX}=\frac{0,8.20}{1}=16\) (m)
Vậy AB = AY + BY = 16 + 1,6 = 17,6 m.
Hoạt động 1 trang 100 Toán 8 tập 2 Kết nối
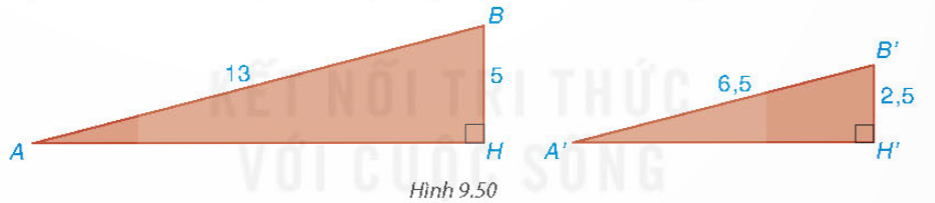
Các tam giác vuông AHB và A'H'B' mô tả hai con dốc có chiều dài lần lượt là AB = 13m, A′B′ = 6,5m và độ cao lần lượt là BH = 5m, B′H′ = 2,5m. Độ dốc của hai con dốc lần lượt được tính bởi số đo các góc HAB và H'A'B'.
- Nhận xét về hai đại lượng \(\frac{A'B'}{AB}\) và \(\frac{B'H'}{BH}\).
- Dùng định lí Pythagore để tính AH và A'H'
- So sánh các đại lượng \(\frac{A'H'}{AH}\) và \(\frac{B'H'}{BH}\).
- Hai tam giác vuông A'H'B' và AHB có đồng dạng không? Từ đó rút ra kết luận gì về độ dốc của hai con dốc.
Hướng dẫn giải:
- Ta có: \(\frac{A'B'}{AB} =\frac{B'H'}{BH} =\frac{1}{2}\)
- Áp dụng định lí Pythagore trong tam giác vuông ta có:
\(AH=\sqrt{13^2-5^2}=12\) m
\(A'H'=\sqrt{6,5^2-2,5^2}=6\) m
- Vậy \(\frac{A'H'}{AH} =\frac{1}{2}=\frac{B'H'}{BH}\)
- Do đó hai tam giác vuông A'H'B' và AHB đồng dạng với nhau (định lí 2).
⇒ \(\widehat{A} = \widehat{A'}\). Vậy hai con dốc có độ dốc như nhau
-----------------------------------------------
Lời giải Toán 8 trang 100 Tập 2 Kết nối tri thức với các câu hỏi nằm trong Giải Toán 8 Kết nối tri thức Bài 36: Các trường hợp đồng dạng của hai tam giác vuông, được VnDoc biên soạn và đăng tải!
