Giải Toán 8 trang 95 tập 2 Kết nối tri thức
Giải Toán 8 trang 95 Tập 2
Giải Toán 8 trang 95 Tập 2 Kết nối tri thức hướng dẫn giải chi tiết cho các câu hỏi và bài tập trong SGK Toán 8 Kết nối tri thức tập 2 trang 95.
Luyện tập 1 trang 95 Toán 8 tập 2 Kết nối
Trên giấy kẻ ô vuông (cạnh ô vuông bằng 1 cm), cho các điểm A, B, C như Hình 9.35. Tính độ dài các cạnh của tam giác ABC.
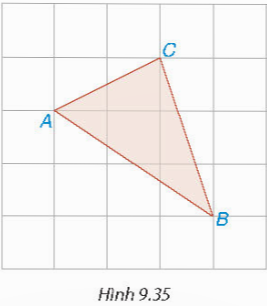
Hướng dẫn giải:
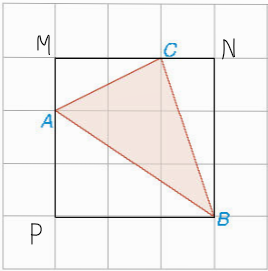
Gọi các điểm M, N, P như hình vẽ.
Áp dụng định lí Pythagore trong tam giác vuông, ta có:
AC2 = 12 + 22 = 5. Suy ra 
\(AC=\sqrt{5}\)
AB2 = 22 + 32 = 13. Suy ra \(AB=\sqrt{13}\)
BC2 = 12 + 32 = 10. Suy ra \(BC=\sqrt{10}\)
Vận dụng 1 trang 95 Toán 8 tập 2 Kết nối
Em hãy giải bài toán mở đầu.
Bài toán: Bạn Lan vẽ một hình chữ nhật với chiều rộng và chiều dài lần lượt là 1; 3 (đơn vị độ dài). Sau đó Lan đặt lên trục số đoạn OM có độ dài bằng độ dài của đường chéo hình chữ nhật vừa vẽ (trục số nằm ngang và M nằm bên phải gốc O). Hỏi điểm M biểu diễn số thực nào? Biết rằng đơn vị độ dài trên trục số và đơn vị độ dài đo kích thước hình chữ nhật là như nhau.
Hướng dẫn giải:
Nếu điểm M biểu diễn số thực x thì OM = x (đvđd)
Đoạn thẳng OM là cạnh huyền của một tam giác vuông với hai cạnh góc vuông là hai cạnh của hình chữ nhật. Áp dụng định lí Pythagore trong tam giác vuông, ta có: x2 = 12 + 32.
Suy ra \(x=\sqrt{10}\).
Vậy M biểu diện số thực \(\sqrt{10}\).
Luyện tập 2 trang 95 Toán 8 tập 2 Kết nối
Cho tam giác vuông với kích thước như Hình 9.37. Hãy tính độ dài x và cho biết những tam giác nào đồng dạng, viết đúng kí hiệu đồng dạng.
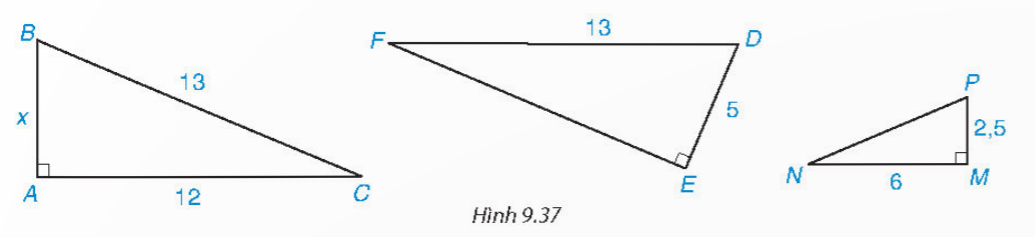
Hướng dẫn giải:
Áp dụng định lí Pythagore trong tam giác vuông ABC, ta có:
x2 + 122 = 132.
⇒ x = 5.
Vậy ∆ ABC = ∆ EDF (cạnh huyền - cạnh góc vuông) (1)
Xét tam giác ABC và tam giác MPN có:
\(\frac{AB}{MP}=\frac{AC}{MN}=2\)
\(\widehat{BAC}= \widehat{PMN}\)
⇒ ∆ ABC ∽ ∆ MPN (c.g.c) với hệ số đồng dạng k = 2 (2)
Từ (1) và (2) suy ra ∆ EDF ∽ ∆ MPN.
-----------------------------------------------
Lời giải Toán 8 trang 95 Tập 2 Kết nối tri thức với các câu hỏi nằm trong Giải Toán 8 Kết nối tri thức Bài 35: Định lí Pythagore và ứng dụng, được VnDoc biên soạn và đăng tải!
