Nguyên lí chồng chất điện trường: Khái niệm, công thức và ví dụ dễ hiểu
Công thức chồng chất điện trường
Nguyên lí chồng chất điện trường là một khái niệm quan trọng trong chương trình Vật lý lớp 11, giúp học sinh hiểu được cách tổng hợp nhiều điện trường tại cùng một điểm trong không gian. Bài viết này sẽ cung cấp cho bạn kiến thức đầy đủ và dễ hiểu nhất về khái niệm, công thức và cách áp dụng nguyên lí chồng chất điện trường, kèm theo ví dụ minh họa rõ ràng và chi tiết. Nếu bạn đang gặp khó khăn với dạng bài này, thì đây chính là tài liệu bạn cần!
A. Nguyên lí chồng chất điện trường
Nguyên lý chồng chất điện trường (hay còn gọi là nguyên lý chồng chất các vectơ điện trường) là một nguyên lý cơ bản trong tĩnh điện học, mô tả cách tính tổng điện trường tại một điểm do nhiều điện tích điểm gây ra.
Phát biểu nguyên lí:
Điện trường tổng hợp tại một điểm do nhiều điện tích điểm gây ra bằng tổng vectơ các điện trường riêng rẽ do từng điện tích gây ra tại điểm đó.
Giả sử có n điện tích điểm 
\(q_{1};q_{2};...;q_{n}\) gây ra các điện trường tại điểm M là \(\overset{\rightarrow}{E_{1}};\overset{\rightarrow}{E_{2}};.....\overset{\rightarrow}{;E_{n}}\) thì:
\(\overset{\rightarrow}{E} =
\overset{\rightarrow}{E_{1}} + \overset{\rightarrow}{E_{2}} +
.....\overset{\rightarrow}{+ E_{n}}\)
Trong đó
\(\overset{\rightarrow}{E_{i}} =
k.\frac{q_{i}}{{r_{i}}^{2}}.\overset{\rightarrow}{u_{i}}\) với
- \(k\) là hằng số điện trường \(k \approx 9.10^{9}\left( \frac{Nm^{2}}{C^{2}}
\right)\)
- \(r_{i}\) là khoảng cách từ \(q_{i}\) đến điểm đang xét
- \(\overset{\rightarrow}{u_{i}}\) là vecto đơn vị theo phương từ \(q_{i}\) đến điểm đang xét
- Dấu \(q_{i}\) xác định chiều của \(\overset{\rightarrow}{E_{i}}\):
-
- Nếu \(q_{i} > 0\) thì vecto hướng ra.
- Nếu \(q_{i} < 0\) thì vecto hướng vào.
- Nếu
Xét trường hợp tại điểm đang xét chỉ có 2 cường độ điện trường
- \(\overrightarrow{E} =
{\overrightarrow{E}}_{1} + {\overrightarrow{E}}_{2}\)
- \({\overrightarrow{E}}_{1} \uparrow
\uparrow {\overrightarrow{E}}_{2} \Rightarrow E = E_{1} +
E_{2}\)
- \({\overrightarrow{E}}_{1} \uparrow
\downarrow {\overrightarrow{E}}_{2} \Rightarrow E = \left| E_{1} - E_{2}
\right|\)
- \({\overrightarrow{E}}_{1}\bot{\overrightarrow{E}}_{2}
\Rightarrow E = \sqrt{E_{1}^{2} + E_{2}^{2}}\)
- \(\left(
{\overrightarrow{E}}_{1},{\overrightarrow{E}}_{2} \right) = \alpha
\Rightarrow E = \sqrt{E_{1}^{2} + E_{2}^{2} +
2E_{1}E_{2}\cos\alpha}\)
- Nếu \(E_{1} = E_{2} \Rightarrow E =
2E_{1}\cos\frac{\alpha}{2}\)
B. Bài tập áp dụng nguyên lí chồng chất điện trường
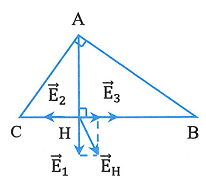
Bài 1: Tại ba đỉnh của một tam giác vuông tại A cạnh \(a = 50cm,\ b = 40cm,\ c = 30cm\) ta đặt lần lượt các điện tích \(q_{1} = q_{2} = q_{3} =
10^{- 9}C\). Xác định vectơ cường độ điện trường tại H, với H là chân đường cao kẻ từ A.
A. \(E_{H} = 246(V/m)\) B. \(E_{H} = 312(V/m)\)
C. \(E_{H} = 123(V/m).\) D. \(E_{H} = 123\sqrt{2}(V/m).\)
Lời giải
Cường độ điện trường tổng hợp tại H là \(\overrightarrow{E_{H}} = \overrightarrow{E_{1}} +
\overrightarrow{E_{2}} + \overrightarrow{E_{3}}\) với phương, chiều được biểu diễn trên hình vẽ.
Dựa vào hệ thức lượng trong tam giác vuông, ta có \(CH = \frac{b^{2}}{a} = \frac{40^{2}}{50} =
32(cm)\).
Ta có \(BH = a - HC = 50 - 32 =
18(cm)\)
Suy ra \(AH = \sqrt{HB.HC} =
24(cm)\) .
Vì \(\overrightarrow{E_{2}} \uparrow
\downarrow \overrightarrow{E_{3}}\), \(\overrightarrow{E_{1}}\) vuông góc với \(\overrightarrow{E_{23}}\) nên ta có độ lớn của cường độ điện trường tại H là
\(E_{H} = \sqrt{E_{1}^{2} + \left( E_{2} -
E_{3} \right)^{2}} = \sqrt{\left( \frac{k\left| q_{1} \right|}{AH^{2}}
\right)^{2} + \left( \frac{k\left| q_{2} \right|}{BH^{2}} -
\frac{k\left| q_{3} \right|}{CH^{2}} \right)^{2}}\)
Thay số ta được \(E_{H} =
246(V/m)\).
Đáp án A.
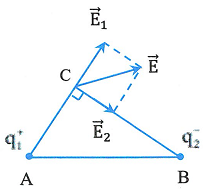
Bài 2: Tại hai điểm A và B cách nhau 5 cm trong chân không có hai điện tích \(q_{1} = 16.10^{- 8}C,\ q_{2} = -
9.10^{- 8}C\). Tìm cường độ điện trường tổng hợp và vẽ vectơ cường độ điện trường tại điểm C nằm cách A một khoảng 4 cm, cách B một khoảng 3 cm.
A. \(E_{C} = 8,98.10^{5}(V/m).\) B. \(E_{C} = 11.10^{5}(V/m).\)
C. \(E_{C} = 12,7.10^{5}(V/m).\) D. \(E_{C} = 6,35.10^{5}(V/m).\)
Lời giải
Điểm C cách A một khoảng 4 cm cách B một khoảng 3 cm thì tam giác ABC là tam giác vuông tại C.
Cường độ điện trường tại C là \(\overrightarrow{E_{C}} = \overrightarrow{E_{1}} +
\overrightarrow{E_{2}}\)
Vì \(\overrightarrow{E_{1}}\) vuông góc với \(\overrightarrow{E_{2}} \Rightarrow
E_{C} = \sqrt{E_{1}^{2} + E_{2}^{2}} = \sqrt{\left( \frac{k\left| q_{1}
\right|}{AC^{2}} \right)^{2} + \left( \frac{k\left| q_{2}
\right|}{BC^{2}} \right)^{2}}\)
Thay số ta được \(E_{C} =
12,7.10^{5}(V/m).\)
Đáp án C.
Bài 3: Trong chân không, một điện tích điểm \(q = 2.10^{- 8}C\) đặt tại một điểm M trong điện trường của một điện tích điểm \(Q =
2.10^{- 6}C\) chịu tác dụng của một lực điện \(F = 9.10^{- 3}\ N\). Tính cường độ điện trường tại M và khoảng cách giữa hai điện tích?
A. \(E_{M} = 90.10^{4}(V/m),\ \ r = 0,141\
(m).\)
B. \(E_{M} =
45\sqrt{2}.10^{4}(V/m),\ \ r = 0,17\ (m).\)
C. \(E_{M} = 45.10^{4}(V/m),\ \ r = 0,2\
(m).\)
D. \(E_{M} =
45\sqrt{3}.10^{4}(V/m),\ \ r = 0,15\ (m).\)
Lời giải
Cường độ điện trường tại M là \(E =
k.\frac{|Q|}{r^{2}} = \frac{F}{q} = 45.10^{4}(V/m)\)
Khoảng cách giữa hai điện tích xác định bởi \(r = \sqrt{\frac{k|Q|}{E}} = 0,2(m)\)
Đáp án C.
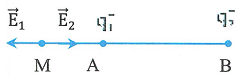
Bài 4: Trong chân không có hai điện tích điểm \(q_{1} = 2.10^{- 8}C,\ q_{2} = - 32.10^{-
8}C\) đặt tại hai điểm A và B cách nhau một khoảng 30 cm. Xác định vị trí điểm M tại đó cường độ điện trường bằng không.
A. M là trung điểm của AB.
B. M nằm trên đường thẳng AB và nằm ngoài đoạn AB, thỏa mãn \(MA = 10\ cm,\ MB = 40\ cm\).
C. M nằm trên đường thẳng AB và nằm ngoài đoạn AB, thỏa mãn \(MA = 40\ cm,\ MB = 10\ cm\).
D. M nằm trên đường thẳng AB và nằm trong đoạn AB, thỏa mãn \(MA = 10\ cm,\ MB = 20\ cm\).
Lời giải
Cường độ điện trường tại M là \(\overrightarrow{E_{M}} = \overrightarrow{E_{1}} +
\overrightarrow{E_{2}} = \overrightarrow{0} \Rightarrow
\overrightarrow{E_{1}} = - \overrightarrow{E_{2}}\), mặt khác 2 điện tích điểm trái dấu với nhau nên từ đây suy ra được M phải nằm ngoài đoạn AB (hình vẽ). Ta có:
\(E_{1} = E_{2} \Rightarrow \frac{\left|
q_{1} \right|}{MA^{2}} = \frac{\left| q_{2} \right|}{MB^{2}} \Rightarrow
\frac{MB^{2}}{MA^{2}} = \frac{32}{2} = 16 \Rightarrow MB = 4MA\) \((1)\)
Vì M nằm ngoài AB nên \(MB - MA =
30(cm)\) \((2)\)
Từ \((1)\) và \((2)\) \(\Rightarrow MA = 10\ cm,\ MB = 40\ cm\)
Đáp án B.
-------------------------------------------
Trên đây là toàn bộ kiến thức về nguyên lí chồng chất điện trường bao gồm định nghĩa, công thức tổng hợp điện trường và cách áp dụng vào bài tập. Hy vọng qua bài viết, bạn đã hiểu rõ và có thể vận dụng tốt trong các bài thi, kiểm tra. Đừng quên ôn luyện thêm nhiều dạng bài tập liên quan để ghi nhớ kiến thức lâu hơn. Chúc bạn học tốt và đạt kết quả cao trong môn Vật lý!
