35 Bài toán thực tế quan hệ vuông góc trong không gian
Toán lớp 11
Tìm hiểu thêm
Tặng thêm 15 ngày khi mua gói 4 tháng.
CHUYÊN ĐỀ 17_THỰC TẾ QUAN HỆ VUÔNG GÓC
A. KIẾN THỨC CẨN NHỚ
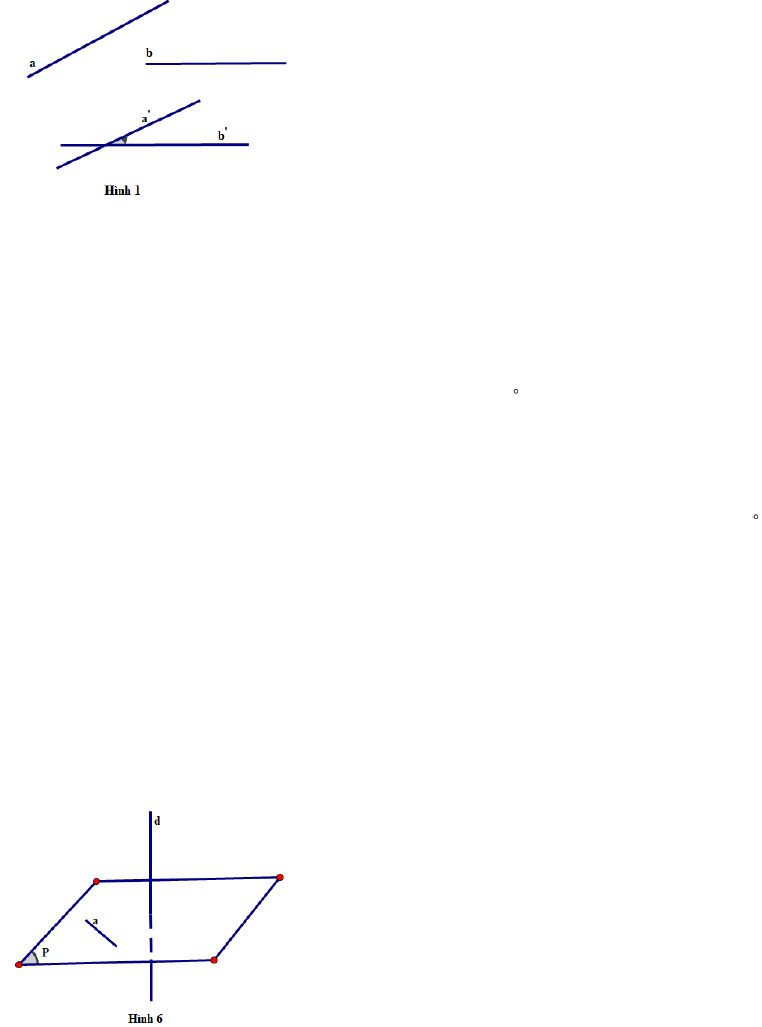
1. Góc giữa hai đường thẳng trong không gian
Góc giữa hai đường thẳng
a và b
trong không gian là góc giữa hai đường thẳng
a
và
b
cùng đi qua một điểm
O
và lần lượt song song (hoặc trùng) với
a và b
(Hình 1), kí hiệu
,ab
hoặc
,ab
.
Nhận xét
Góc giữa hai đường thẳng
,ab
không phụ thuộc vào vị trí điểm
O
. Thông thường, khi tìm góc giữa hai
đường thẳng
,ab
, ta chọn
O
thuộc
a
hoặc
O
thuộc
b
.
Góc giữa hai đường thẳng
,ab
bằng góc giữa hai đường thẳng
,ba
, tức là
,,a b b a
.
Góc giữa hai đường thẳng không vượt quá
90
.
Nếu
//ab
thì
,,a c b c
với mọi đường thẳng
c
trong không gian.
2. Hai đường thẳng vuông góc trong không gian
Hai đường thẳng được gọi là vuông góc với nhau nếu góc giữa chúng bằng
90
.
Khi hai đường thẳng
a
và
b
vuông góc với nhau, ta kí hiệu
ab
.
Nhận xét: Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó vuông góc với đường
còn lại.
3. Đường thẳng vuông góc với mặt phẳng
Đường thẳng
d
được gọi là vuông góc với mặt phẳng
P
nếu đường thẳng
d
vuông góc với mọi đường thẳng
a
nằm trong mặt phẳng
P
(Hình 6), kí hiệu
dP
hoặc
Pd
.
4. Điều kiện để đường thẳng vuông góc với mặt phẳng
Nếu một đường thẳng vuông góc với hai đường thẳng cắt nhau cùng thuộc một mặt phẳng thì nó vuông góc với
mặt phẳng ấy.
Nhận xét: Ta có thể chứng minh hai đường thẳng vuông góc bằng cách chứng minh một đường thẳng vuông góc
với một mặt phẳng chứa đường thẳng kia.
5. Tính chất
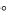
Tính chất 1: Có duy nhất một mặt phẳng đi qua một điểm cho trước và vuông góc với một đường thẳng
cho trước.
Tính chất 2: Có duy nhất một đường thẳng đi qua một điểm cho trước và vuông góc với một mặt phẳng
cho trước.
6. Liên hệ giữa quan hệ song song và quan hệ vuông góc của đường thẳng và mặt phẳng
Tính chất 3:
Cho hai đường thẳng song song. Một mặt phẳng vuông góc với đường thẳng này thì cũng vuông góc với đường
thẳng kia.
Hai đường thẳng phân biệt cùng vuông góc với một mặt phẳng thì song song với nhau.
Tính chất 4:
Cho hai mặt phẳng song song. Một đường thẳng vuông góc với mặt phẳng này thì cũng vuông góc với mặt phẳng
kia.
Hai mặt phẳng phân biệt cùng vuông góc với một đường thẳng thì song song với nhau.
7. Phép chiếu vuông góc
Cho mặt phẳng
P
và một điểm
M
tuỳ ý trong không gian. Lấy đường thẳng đi qua
M
và vuông góc với
P
,
gọi giao điểm của
d
và
P
là
M
. Điểm
M
gọi là hình chiếu vuông góc (hay hình chiếu) của điểm
M
trên
P
.
Cho mặt phẳng
P
. Quy tắc đặt tương ứng mỗi điểm
M
trong không gian với hình chiếu vuông góc
M
của
điểm đó lên mặt phẳng
P
được gọi là phép chiếu vuông góc lên mặt phẳng
P
.
Nhận xét: Vì phép chiếu vuông góc là một trường hợp đặc biệt của phép chiếu song song (khi phương chiếu
vuông góc với mặt phẳng chiếu) nên phép chiếu vuông góc có đầy đủ các tính chất của phép chiếu song song.
8. Định lí ba đường vuông góc
Cho đường thẳng
a
không vuông góc với mặt phẳng
P
và đường thẳng
d
nằm trong mặt phẳng
P
. Khi đó,
d
vuông góc với
a
khi và chỉ khi
d
vuông góc với hình chiếu
a
của
a
trên
P
.
9. Góc giữa đường thẳng và mặt phẳng
Cho đường thẳng
d
và mặt phẳng
P
, ta có định nghĩa sau:
Nếu đường thẳng
d
vuông góc với mặt phẳng
P
thì góc giữa
d
và
P
bằng
90
.
Nếu đường thẳng
d
không vuông góc với mặt phẳng
P
thì góc giữa đường thẳng
d
và mặt phẳng
P
là góc giữa
d
và hình chiếu
'd
của đường thẳng
d
trên
P
.
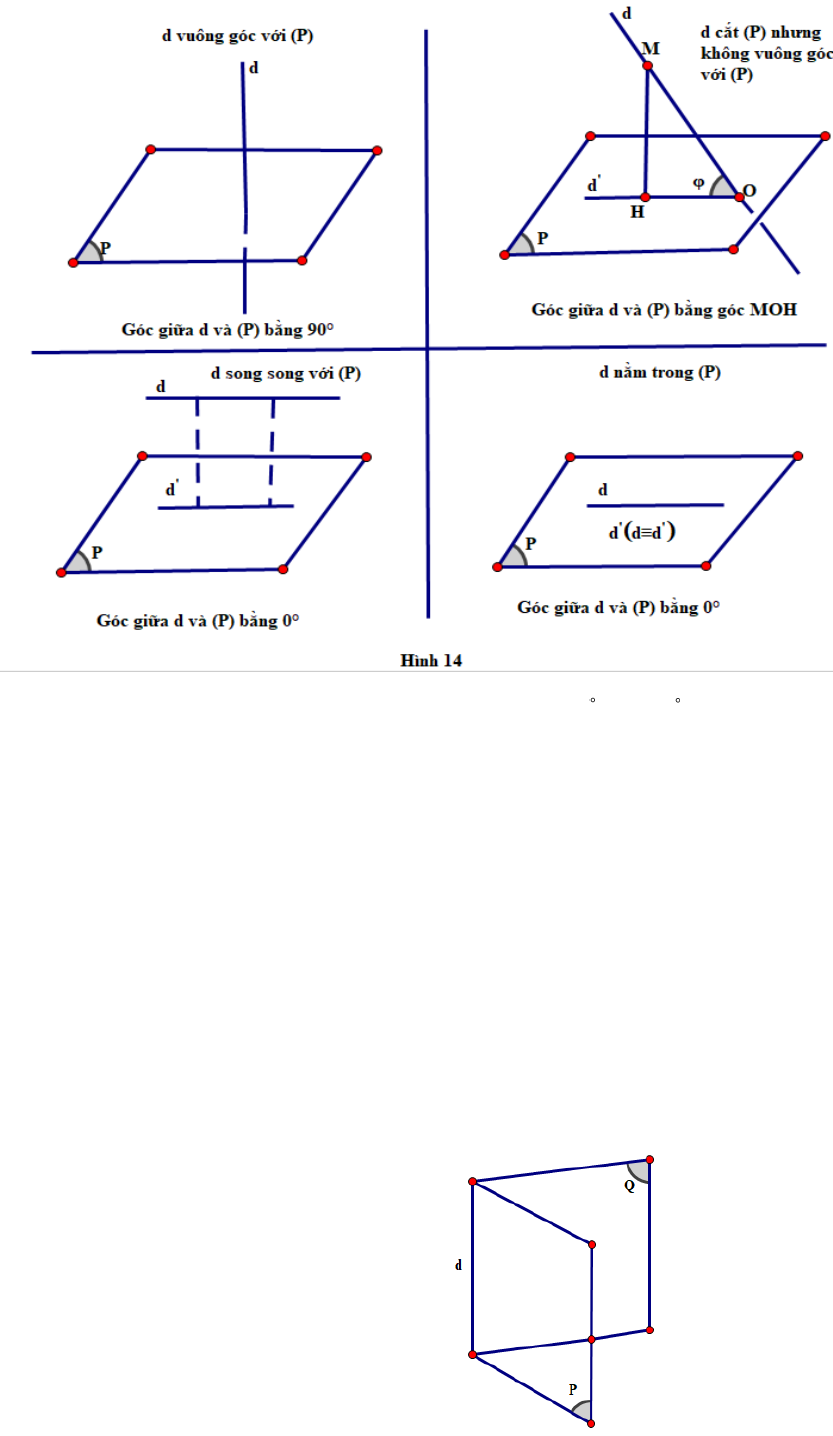
Nhận xét: Góc giữa đường thẳng và mặt phẳng có số đo từ
0
đến
90
(Hình 14).
10. Góc nhị diện
a) Nửa mặt phẳng
Một đường thẳng nằm trong mặt phẳng chia mặt phẳng đó thành hai phần, mỗi phần được gọi là một nửa mặt
phẳng và đường thẳng đó được gọi là bờ của mỗi nửa mặt phẳng này.
b) Góc nhị diện
Góc nhị diện là hình gồm hai nửa mặt phẳng có chung bờ.
Ví dụ: Xét góc nhị diện gồm hai nửa mặt phẳng
P
và
Q
có chung bờ là đường thả
̉
ng
d
(Hình 15
)
, kí hiệu là
,,M d N
. Đường thẳng
d
gọi là cạnh của góc nhị diện, mỗi nửa mặt phẳng
P
và
Q
gọi là một mặt của góc nhị
diện.
Các dạng bài toán quan hệ vuông góc trong không gian
35 Bài toán thực tế về quan hệ vuông góc trong không gian được VnDoc.com tổng hợp và xin gửi tới bạn đọc cùng tham khảo. Bài viết được tổng hợp gồm có 2 phần: Lý thuyết kiến thức cần nhớ về quan hệ vuông góc và phần bài tập vận dụng 35 câu hỏi có đáp án kèm theo. Mời các bạn cùng theo dõi bài viết dưới đây để có thêm tài liệu học Toán lớp 11 nhé.
