Công thức tính cường độ điện trường tổng hợp
Cách tính cường độ điện trường tổng hợp
Cường độ điện trường là một trong những khái niệm nền tảng trong Vật lý, đặc biệt quan trọng trong chương trình học THPT và ôn thi đại học. Trong bài viết này, chúng ta sẽ cùng tìm hiểu công thức tính cường độ điện trường tổng hợp – một kiến thức không thể bỏ qua khi làm các bài tập về điện trường nhiều điện tích. Bài viết sẽ cung cấp công thức, cách áp dụng và ví dụ minh họa giúp bạn dễ dàng nắm bắt và vận dụng hiệu quả.
1. Cường độ điện trường tổng hợp
Gọi ![]() \(\overrightarrow{E_{1}},\overrightarrow{E_{2}},\overrightarrow{E_{3}},...\) là điện trường do điện tích
\(\overrightarrow{E_{1}},\overrightarrow{E_{2}},\overrightarrow{E_{3}},...\) là điện trường do điện tích ![]() \(q_{1},q_{2},q_{3},...\) gây ra tại điểm M.
\(q_{1},q_{2},q_{3},...\) gây ra tại điểm M.
Cường độ điện trường tổng hợp tại M do ![]() \(q_{1},q_{2},q_{3},...\) gây ra là:
\(q_{1},q_{2},q_{3},...\) gây ra là:
![]() \(\boxed{\overrightarrow{E} =
\overrightarrow{E_{1}} + \overrightarrow{E_{2}} + \overrightarrow{E_{3}}
+ ...}\)
\(\boxed{\overrightarrow{E} =
\overrightarrow{E_{1}} + \overrightarrow{E_{2}} + \overrightarrow{E_{3}}
+ ...}\)
Thông thường ta sẽ gặp hai hoặc ba điện tích gây ra điện trường tại điểm M.
Để xác định cường độ điện trường tổng hợp ![]() \(\overrightarrow{E}\) ta có thể xác định theo một trong hai cách sau:
\(\overrightarrow{E}\) ta có thể xác định theo một trong hai cách sau:
Cách 1: Sử dụng cộng vectơ theo quy tắc hình bình hành, tính toán dựa trên hình.
Nếu ![]() \(\overrightarrow{E_{1}},\overrightarrow{E_{2}}\) cùng phương và:
\(\overrightarrow{E_{1}},\overrightarrow{E_{2}}\) cùng phương và:
 \(\overrightarrow{E_{1}},\overrightarrow{E_{2}}\) cùng chiều thì:
\(\overrightarrow{E_{1}},\overrightarrow{E_{2}}\) cùng chiều thì:  \(E = E_{1} +
E_{2}\).
\(E = E_{1} +
E_{2}\).
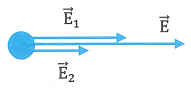
 \(\overrightarrow{E_{1}},\overrightarrow{E_{2}}\) ngược chiều thì:
\(\overrightarrow{E_{1}},\overrightarrow{E_{2}}\) ngược chiều thì:  \(E = \left| E_{1} -
E_{2} \right|\).
\(E = \left| E_{1} -
E_{2} \right|\).
![]()
Nếu ![]() \(\overrightarrow{E_{1}},\overrightarrow{E_{2}}\) có phương vuông góc thì
\(\overrightarrow{E_{1}},\overrightarrow{E_{2}}\) có phương vuông góc thì ![]() \(E = \sqrt{E_{1}^{2} +
E_{2}^{2}}\)
\(E = \sqrt{E_{1}^{2} +
E_{2}^{2}}\)
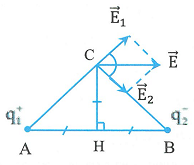
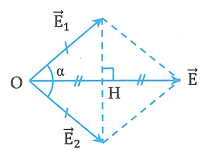
Nếu ![]() \(\overrightarrow{E_{1}},\overrightarrow{E_{2}}\) có cùng độ lớn và hợp với nhau một góc
\(\overrightarrow{E_{1}},\overrightarrow{E_{2}}\) có cùng độ lớn và hợp với nhau một góc ![]() \(\alpha\) thì
\(\alpha\) thì ![]() \(E = 2OH \Rightarrow \boxed{E =
2E_{1}\cos\frac{\alpha}{2}}\)
\(E = 2OH \Rightarrow \boxed{E =
2E_{1}\cos\frac{\alpha}{2}}\)
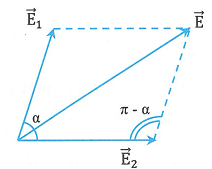
Nếu ![]() \(\overrightarrow{E_{1}},\overrightarrow{E_{2}}\) khác độ lớn và hợp với nhau một góc
\(\overrightarrow{E_{1}},\overrightarrow{E_{2}}\) khác độ lớn và hợp với nhau một góc ![]() \(\alpha\) thì
\(\alpha\) thì
![]() \(E^{2} = E_{1}^{2} + E_{2}^{2} -
2E_{1}E_{2}\cos(\pi - \alpha)\)
\(E^{2} = E_{1}^{2} + E_{2}^{2} -
2E_{1}E_{2}\cos(\pi - \alpha)\)
![]() \(\Rightarrow \boxed{E^{2} = E_{1}^{2} +
E_{2}^{2} + 2E_{1}E_{2}\cos\alpha}\)
\(\Rightarrow \boxed{E^{2} = E_{1}^{2} +
E_{2}^{2} + 2E_{1}E_{2}\cos\alpha}\)
Cách 2: Phương pháp hình chiếu.
Chọn hệ trục tọa độ Oxy vuông góc và ta chiếu các vectơ lên các trục tọa độ, ta thu được:
![]() \(\left\{ \begin{matrix}
E_{x} = E_{1x} + E_{2x} + E_{3x} + E_{4x} + ... \\
E_{y} = E_{1y} + E_{2y} + E_{3y} + E_{4y} + ... \\
\end{matrix} \right.\)
\(\left\{ \begin{matrix}
E_{x} = E_{1x} + E_{2x} + E_{3x} + E_{4x} + ... \\
E_{y} = E_{1y} + E_{2y} + E_{3y} + E_{4y} + ... \\
\end{matrix} \right.\)
Khi đó độ lớn của cường độ điện trường tổng hợp ![]() \(E = \sqrt{E_{x}^{2} + E_{y}^{2}}\).
\(E = \sqrt{E_{x}^{2} + E_{y}^{2}}\).
2. Bài tập tính cường độ điện trường tổng hợp
Bài 1: Cho hai điện tích ![]() \(q_{1} =
4.10^{- 10}\) C,
\(q_{1} =
4.10^{- 10}\) C, ![]() \(q_{2} = - 4.10^{-
10}\) C, đặt tại A và B trong không khí biết
\(q_{2} = - 4.10^{-
10}\) C, đặt tại A và B trong không khí biết ![]() \(AB = 2\)cm. Xác định độ lớn cường độ điện trường
\(AB = 2\)cm. Xác định độ lớn cường độ điện trường ![]() \(\overrightarrow{E}\) (V/m) tại:
\(\overrightarrow{E}\) (V/m) tại:
a) H là trung điểm của AB.
| A. |
B. |
| C. |
D. |
b) M với ![]() \(MA = 1\ cm,\ MB = 3\
cm\).
\(MA = 1\ cm,\ MB = 3\
cm\).
| A. |
B. |
| C. |
D. |
c) N biết rằng NAB là một tam giác đều.
| A. |
B. |
| C. |
D. |
Hướng dẫn giải
a) Ta có: ![]() \(\overrightarrow{E_{H}} =
\overrightarrow{E_{1}} + \overrightarrow{E_{2}}\), vì 2 điện tích
\(\overrightarrow{E_{H}} =
\overrightarrow{E_{1}} + \overrightarrow{E_{2}}\), vì 2 điện tích ![]() \(q_{1}\) và
\(q_{1}\) và ![]() \(q_{2}\) trái dấu nhau nên
\(q_{2}\) trái dấu nhau nên ![]() \(\overrightarrow{E_{1}} \uparrow \uparrow
\overrightarrow{E_{2}}\), từ đó suy ra cường độ điện trường tại H là
\(\overrightarrow{E_{1}} \uparrow \uparrow
\overrightarrow{E_{2}}\), từ đó suy ra cường độ điện trường tại H là
![]() \(E_{H} = E_{1} + E_{2} = k\left(
\frac{\left| q_{1} \right|}{AH^{2}} + \frac{\left| q_{2}
\right|}{BH^{2}} \right)\) , với
\(E_{H} = E_{1} + E_{2} = k\left(
\frac{\left| q_{1} \right|}{AH^{2}} + \frac{\left| q_{2}
\right|}{BH^{2}} \right)\) , với ![]() \(AH =
BH = \frac{AB}{2} = 1\)(cm).
\(AH =
BH = \frac{AB}{2} = 1\)(cm).
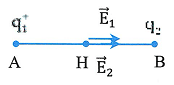
Thay số ta được: ![]() \(E_{H} =
72.10^{3}.\) (V/m). Vậy vectơ cường độ điện trường tại H có:
\(E_{H} =
72.10^{3}.\) (V/m). Vậy vectơ cường độ điện trường tại H có:
+ Điểm đặt: Tại H
+ Phương: trùng với đường thẳng AB
+ Chiều: từ A đến B
+ Độ lớn: ![]() \(E_{H} = 72.10^{3}\) (V/m)
\(E_{H} = 72.10^{3}\) (V/m)
b) ![]() \(\overrightarrow{E_{M}} =
\overrightarrow{E_{1}} + \overrightarrow{E_{2}}\)
\(\overrightarrow{E_{M}} =
\overrightarrow{E_{1}} + \overrightarrow{E_{2}}\)
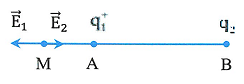
Vì ![]() \(AM = AB + BM\) nên M nằm trên đường thẳng AB ngoài đoạn AB về phía A
\(AM = AB + BM\) nên M nằm trên đường thẳng AB ngoài đoạn AB về phía A
Nên từ đó ta được ![]() \(\overrightarrow{E_{1}}
\uparrow \downarrow \overrightarrow{E_{2}} \Rightarrow E_{M} = \left|
E_{1} - E_{2} \right|\). Hay
\(\overrightarrow{E_{1}}
\uparrow \downarrow \overrightarrow{E_{2}} \Rightarrow E_{M} = \left|
E_{1} - E_{2} \right|\). Hay
![]() \(E_{M} = k\left( \frac{\left| q_{1}
\right|}{AM^{2}} - \frac{\left| q_{2} \right|}{BM^{2}} \right) =
32.10^{3}\) (V/m)
\(E_{M} = k\left( \frac{\left| q_{1}
\right|}{AM^{2}} - \frac{\left| q_{2} \right|}{BM^{2}} \right) =
32.10^{3}\) (V/m)
Vậy vectơ cường độ điện trường tại M
+ Điểm đặt: Tại M
+ Phương: đường thẳng AB
+ Chiều: hướng ra xa A
+ Độ lớn: ![]() \(E_{M} = 32.10^{3}\) (V/m)
\(E_{M} = 32.10^{3}\) (V/m)
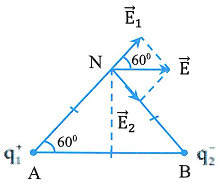
c) ![]() \(\overrightarrow{E_{N}} =
\overrightarrow{E_{1}} + \overrightarrow{E_{2}}\)
\(\overrightarrow{E_{N}} =
\overrightarrow{E_{1}} + \overrightarrow{E_{2}}\)
Vì ![]() \(\left| q_{1} \right| = \left| q_{2}
\right|,\ \ NA = NB = 2cm,\ \ \left(
\overrightarrow{E_{1}},\overrightarrow{E_{2}} \right) = 120^{0}\) nên ta có cường độ điện trường tổng hợp có độ lớn là
\(\left| q_{1} \right| = \left| q_{2}
\right|,\ \ NA = NB = 2cm,\ \ \left(
\overrightarrow{E_{1}},\overrightarrow{E_{2}} \right) = 120^{0}\) nên ta có cường độ điện trường tổng hợp có độ lớn là
![]() \(E_{N} = E_{1} = E_{2} =
\frac{9.10^{9}.4.10^{- 10}}{0,02^{2}} = 9.10^{3}\) (V/m)
\(E_{N} = E_{1} = E_{2} =
\frac{9.10^{9}.4.10^{- 10}}{0,02^{2}} = 9.10^{3}\) (V/m)
Vậy vectơ cường độ điện trường tại N
+ Điểm đặt: Tại N
+ Phương: song song với AB
+ Chiều: từ A đến B
+ Độ lớn: ![]() \(E_{N} = 9.10^{3}\) (V/m)
\(E_{N} = 9.10^{3}\) (V/m)
Bài 2: Hai điện tích ![]() \(q_{1} = 8.10^{-
8}C,\ q_{2} = - 8.10^{- 8}C\) đặt tại A và B trong không khí biết
\(q_{1} = 8.10^{-
8}C,\ q_{2} = - 8.10^{- 8}C\) đặt tại A và B trong không khí biết ![]() \(AB = 4\ cm\). Tìm cường độ điện trường tại C trên đường trung trực của AB và cách AB 2cm và lực tác dụng lên điện tích
\(AB = 4\ cm\). Tìm cường độ điện trường tại C trên đường trung trực của AB và cách AB 2cm và lực tác dụng lên điện tích ![]() \(q = 2.10^{- 9}C\) đặt tại C.
\(q = 2.10^{- 9}C\) đặt tại C.
A. ![]() \(E_{N} = 9\sqrt{2}.10^{5}\
(V/m)\), lực tác dụng
\(E_{N} = 9\sqrt{2}.10^{5}\
(V/m)\), lực tác dụng ![]() \(F = 2,55.10^{-
3}(N)\).
\(F = 2,55.10^{-
3}(N)\).
B. ![]() \(E_{N} = 9\sqrt{3}.10^{5}\
(V/m)\), lực tác dụng
\(E_{N} = 9\sqrt{3}.10^{5}\
(V/m)\), lực tác dụng ![]() \(F = 3,12.10^{-
3}(N)\).
\(F = 3,12.10^{-
3}(N)\).
C. ![]() \(E_{N} = 4,5\sqrt{3}.10^{5}\
(V/m)\), lực tác dụng
\(E_{N} = 4,5\sqrt{3}.10^{5}\
(V/m)\), lực tác dụng ![]() \(F = 1,55.10^{-
3}(N)\).
\(F = 1,55.10^{-
3}(N)\).
D. ![]() \(E_{N} = 4,5\sqrt{2}.10^{5}\
(V/m)\), lực tác dụng
\(E_{N} = 4,5\sqrt{2}.10^{5}\
(V/m)\), lực tác dụng ![]() \(F = 1,27.10^{-
3}(N)\).
\(F = 1,27.10^{-
3}(N)\).
Hướng dẫn giải
Gọi góc hợp bởi ![]() \(\left(
\overrightarrow{E_{1}},\overrightarrow{E_{2}} \right) = \alpha\), trung điểm AB là H
\(\left(
\overrightarrow{E_{1}},\overrightarrow{E_{2}} \right) = \alpha\), trung điểm AB là H
Cường độ điện trường tổng hợp tại C là ![]() \(\overrightarrow{E_{C}} = \overrightarrow{E_{1}} +
\overrightarrow{E_{2}}\)
\(\overrightarrow{E_{C}} = \overrightarrow{E_{1}} +
\overrightarrow{E_{2}}\)
Vì ![]() \(\left| q_{1} \right| = \left| q_{2}
\right|,\ \ CA = CB = \sqrt{CH^{2} + AH^{2}}\) nên dựa vào hình vẽ, ta có
\(\left| q_{1} \right| = \left| q_{2}
\right|,\ \ CA = CB = \sqrt{CH^{2} + AH^{2}}\) nên dựa vào hình vẽ, ta có
![]() \(\cos\frac{\alpha}{2} = \cos A =
\frac{AH}{CA} = \frac{AH}{\sqrt{CH^{2} + AH^{2}}} = \frac{2}{\sqrt{2^{2}
+ 2^{2}}} = \frac{1}{\sqrt{2}}\)
\(\cos\frac{\alpha}{2} = \cos A =
\frac{AH}{CA} = \frac{AH}{\sqrt{CH^{2} + AH^{2}}} = \frac{2}{\sqrt{2^{2}
+ 2^{2}}} = \frac{1}{\sqrt{2}}\)
Từ đây suy ra
![]() \(E_{C} = 2E_{1}\cos\frac{\alpha}{2} =
\sqrt{2}E_{1} = \sqrt{2}.k.\frac{\left| q_{1} \right|}{CA^{2}} =
\frac{\sqrt{2}.9.10^{9}.8.10^{- 8}}{8.10^{- 4}} =
9\sqrt{2}.10^{5}(V/m)\)
\(E_{C} = 2E_{1}\cos\frac{\alpha}{2} =
\sqrt{2}E_{1} = \sqrt{2}.k.\frac{\left| q_{1} \right|}{CA^{2}} =
\frac{\sqrt{2}.9.10^{9}.8.10^{- 8}}{8.10^{- 4}} =
9\sqrt{2}.10^{5}(V/m)\)
Vậy vectơ cường độ điện trường tại C
+ Điểm đặt: Tại C
+ Phương: song song với AB
+ Chiều: từ A đến B
+ Độ lớn: ![]() \(E_{N} = 9\sqrt{2}.10^{5}\
(V/m)\)
\(E_{N} = 9\sqrt{2}.10^{5}\
(V/m)\)
Suy ra lực tác dụng lên điện tích q đặt tại C là
![]() \(F = |q|E_{C} = 2.10^{-
9}.9\sqrt{2}.10^{5} = 2,55.10^{- 3}\ (N)\)
\(F = |q|E_{C} = 2.10^{-
9}.9\sqrt{2}.10^{5} = 2,55.10^{- 3}\ (N)\)