Đề chọn đội tuyển Olympic Toán Đại học Ngoại Thương năm 2013

TRƯỜNG ĐẠI HỌC NGOẠI THƯƠNG HÀ NỘI ĐỀ CHÍNH THỨC

KỲ THI OLYMPIC TOÁN SINH VIÊN 2013 MÔN: TOÁN HỌC

Câu 1.

Cho ma trận: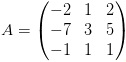

Đặt với E là ma trận đơn vị cấp 3. Tính: lim_n→∞U_n

Câu 2.

Dãy số Fibonaci được định nghĩa bởi F_o = 1; F₁ = 1; F_n1 = F_nF_n-1 nếu n ≥ 1

a) Chứng minh rằng: F²_n - F_n-1F_n1 = (-1)ⁿ nếu n ≥ 1

b) Tính giá trị của

Câu 3.

Với a_i, b_i (i = 1, 2,..., n) là các số thực cho trước đôi một phân biệt. Xét hệ phương trình sau: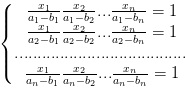

a) Giải hệ phương trình

b) Tính tổng các ngiệm

Câu 4.

Cho là một ma trận thực hoặc phức với các giá trị riêng phân biệt λ₁, λ₂ và các vector riêng tương ứng X₁, X₂. Cho P = [X₁\X₂].

Chứng minh rằng hệ có nghiệm là trong đó α, β được xác định bởi phương trình

Câu 5. Cho ma trận:

Tìm tất cả các ma trận X thỏa mãn A.X = X.A

Câu 6.

Biện luận theo m nghiệm đa thức P(x) của phương trình hàm sau: 1.xP(x) = m[P(x1)P(x - 1)]