Đề thi chọn học sinh giỏi lớp 12 môn Toán cấp cơ sở năm 2018 - 2019 Sở GD&ĐT Điện Biên
Đề thi chọn HSG Toán 12
ĐỀ VÀ HDG HỌC SINH GIỎI 12 ĐIỆN BIÊN 2018-2019
Câu 1: (6,0 điểm)
1. Cho hàm số
2 3
( )
1
−
=
−
x
y C
x
và
đườ
ng th
ẳ
ng
: 1 0
− − =
d x y
. Vi
ế
t ph
ươ
ng trình ti
ế
p tuy
ế
n
c
ủ
a
đồ
th
ị
( )
C
bi
ế
t ti
ế
p tuy
ế
n
đ
ó song song v
ớ
i d.
2.
Tìm
m
để
hàm s
ố
(
)
3 2 2
3 3 1 2
= − + − + +
y x mx m x m
đồ
ng bi
ế
n trên kho
ả
ng
(
)
2;
+∞
.
Câu 2: (4,0 điểm)
1.
Tìm giá tr
ị
l
ớ
n nh
ấ
t và giá tr
ị
nh
ỏ
nh
ấ
t c
ủ
a hàm s
ố
( )
2
4 4
2sin
sin cos
2 2
=
+
x
f x
x x
.
2.
Gi
ả
i h
ệ
ph
ươ
ng trình
(
)
( )
3 3 2 2
3 2 2 15 10 0
;
2 3 2 2
− − − + + − =
∈
− + − = −
ℝ
x y x y y x
x y
y x x
.
Câu 3: (4,0 điểm)
1.
G
ọ
i
S
là t
ậ
p h
ợ
p t
ấ
t c
ả
các s
ố
t
ự
nhiên có 5 ch
ữ
s
ố
khác nhau
đượ
c ch
ọ
n t
ừ
các s
ố
0;1; 2;3; 4;5;6; 7;8;9
. Xác
đị
nh s
ố
ph
ầ
n t
ử
c
ủ
a
S
. Ch
ọ
n ng
ẫ
u nhiên m
ộ
t s
ố
t
ừ
S
,
tính xác su
ấ
t
để
s
ố
đượ
c ch
ọ
n là s
ố
ch
ẵ
n.
2.
Trong m
ặ
t ph
ẳ
ng t
ọ
a
độ
Oxy
cho hai
đ
i
ể
m
(
)
(
)
0;9 , 3;6
A B
. G
ọ
i
D
là mi
ề
n nghi
ệ
m c
ủ
a h
ệ
ph
ươ
ng trình
2 0
6 3 5 0
− + ≤
+ + ≥
x y a
x y a
. Tìm t
ấ
t c
ả
các giá tr
ị
c
ủ
a
a
để
⊂
AB D
.
Câu 4: (4,0 điểm)
1.
Cho hình chóp
SABC
. Trên các
đ
o
ạ
n th
ẳ
ng
, ,
SA SB SC
l
ầ
n l
ượ
t l
ấ
y các
đ
i
ể
m
', ', '
A B C
khác
v
ớ
i
đ
i
ể
m
S
. Ch
ứ
ng minh r
ằ
ng:
.
. ' ' '
. .
' ' '
=
S ABC
S A B C
V
SA SB SC
V SA SB SC
2.
Cho hình chóp t
ứ
giác
đề
u
.
S ABCD
, có
, 3
= =
AB a SA a
. G
ọ
i
O
là giao
đ
i
ể
m c
ủ
a
AC
và
BD
,
G
là tr
ọ
ng tâm tam giác
SCD
.
a) Tính th
ể
tích kh
ố
i chóp
. .
S OGC
b) Tính kho
ả
ng cách t
ừ
G
đế
n m
ặ
t ph
ẳ
ng
(
)
SBC
.
c) Tính cosin góc gi
ữ
a hai
đườ
ng th
ẳ
ng
SA
và
BG
.
Câu 5: (2,0 điểm)
1.
Cho ph
ươ
ng trình
( )
(
)
( ) ( )
2 2
2 1 6 1 0 1
+ + − + − − =m x x x m x
. Tìm các giá tr
ị
c
ủ
a
m
để
ph
ươ
ng trình
(
)
1
có nghi
ệ
m th
ự
c.
2.
Cho
đ
a th
ứ
c
(
)
4 3 2
1
= + + + +
f x x ax bx ax
có nghi
ệ
m th
ự
c. Ch
ứ
ng minh r
ằ
ng
2 2
4 1 0
+ − + >
a b b
.
HDG
Câu 1: (6,0 điểm)
1.
Cho hàm s
ố
2 3
( )
1
−
=
−
x
y C
x
và
đườ
ng th
ẳ
ng
: 1 0
− − =
d x y
. Vi
ế
t ph
ươ
ng trình ti
ế
p tuy
ế
n
c
ủ
a
đồ
th
ị
( )
C
bi
ế
t ti
ế
p tuy
ế
n
đ
ó song song v
ớ
i d.
2.
Tìm
m
để
hàm s
ố
(
)
3 2 2
3 3 1 2
= − + − + +
y x mx m x m
đồ
ng bi
ế
n trên kho
ả
ng
(
)
2;
+∞
.
T
ậ
p xác
đị
nh:
.
ℝ
Lời giải
1.
: 1 0 : 1
− − = ⇒ = − ⇒
d x y d y x
d có h
ệ
s
ố
góc
1.
=
d
k
Xét hàm s
ố
2 3
( )
1
−
= =
−
x
y f x
x
:
+ T
ậ
p xác
đị
nh
{
}
\ 1 .
=
ℝ
D
+
(
)
/
2
1
( ) , x 1.
1
= ∀ ≠
−
f x
x
G
ọ
i
∆
là ti
ế
p tuy
ế
n c
ủ
a
( )
C
t
ạ
i
0
0
0
2 3
x ;
1
−
−
x
M
x
thì
∆
:
/
0
0 0
0
2 3
( )( )
1
−
= − +
−
x
y f x x x
x
+ Gi
ả
s
ử
/ /
∆
d
ta
đượ
c
(
)
0
/
0
2
0
0
0
1
( ) 1
2
1
=
= ⇔ = ⇔
=
−
d
x
f x k
x
x
.
+ Th
ử
l
ạ
i:
0
0 : 3
= ⇒ ∆ = +
i
x y x th
ỏ
a mãn
/ /
∆
d
.
0
2 : 1
= ⇒ ∆ = − ⇒
i
x y x
.
∆ ≡
d
Tr
ườ
ng h
ợ
p này không th
ỏ
a mãn.
V
ậ
y có
đ
úng m
ộ
t ti
ế
p tuy
ế
n c
ủ
a
( )
C
th
ỏ
a
đề
,
đ
ó là
: 3.
∆ = +
y x
2.
2/ 2
3 6 3( 1), x
= − + − ∀ ∈
ℝ
y x mx m
/
1
0
1
= −
= ⇔
= −
x m
y
x m
: Hai nghi
ệ
m phân bi
ệ
t v
ớ
i m
ọ
i
.
m
B
ả
ng bi
ế
n thiên
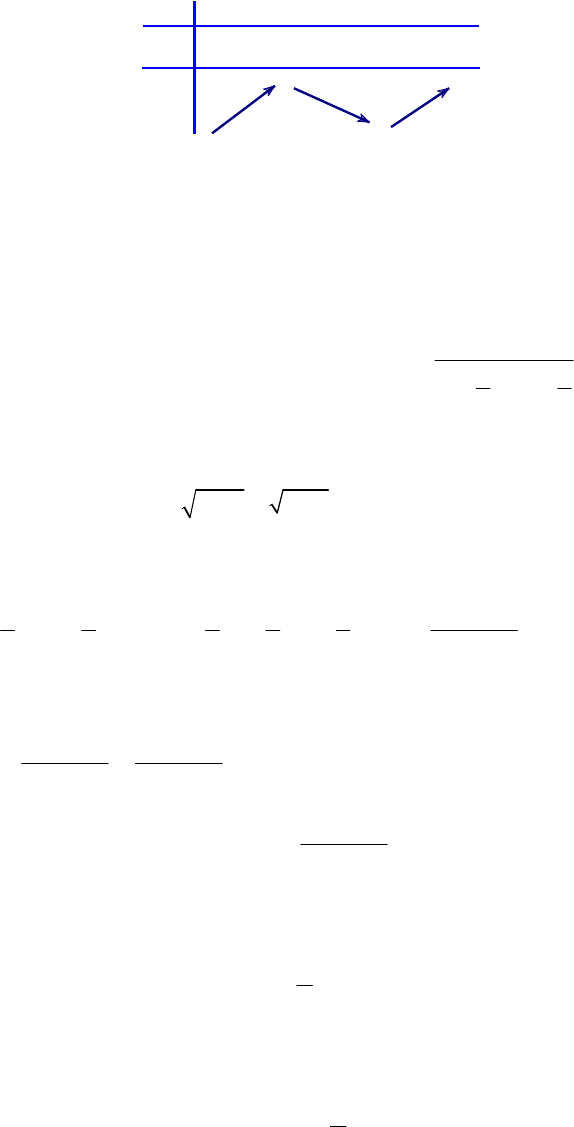
Hàm s
ố
đồ
ng bi
ế
n trên
(
)
(
)
(
)
2; 2; 1; 1 2 1.
+∞ ⇔ +∞ ⊂ + +∞ ⇔ + ≤ ⇔ ≤
m m m
V
ậ
y m c
ầ
n tìm là
1.
≤
m
Câu 2: (4,0 điểm)
1.
Tìm giá tr
ị
l
ớ
n nh
ấ
t và giá tr
ị
nh
ỏ
nh
ấ
t c
ủ
a hàm s
ố
( )
2
4 4
2sin
sin cos
2 2
=
+
x
f x
x x
.
2.
Gi
ả
i h
ệ
ph
ươ
ng trình
(
)
( )
3 3 2 2
3 2 2 15 10 0
;
2 3 2 2
− − − + + − =
∈
− + − = −
ℝ
x y x y y x
x y
y x x
.
Lời giải
1.
Ta có
2
4 4 2 2 2
1 2 sin
sin cos 1 2sin cos 1 sin 0, .
2 2 2 2 2 2
−
+ = − = − = ≠ ∀
x x x x x
x x
Cách 1:
Khi
đ
ó
( )
2
2 2
4sin 8
4
2 sin 2 sin
= = −
− −
x
f x
x x
.
Vì
2 2
0 sin 1 1 2 sin 2
≤ ≤ ⇒ ≤ − ≤
x x
nên
2
8
4 8
2 sin
≤ ≤
−
x
. Do
đ
ó
(
)
0 4
≤ ≤
f x
.
Ta có
(
)
(
)
2
0 sin 0 sin 0
= ⇔ = ⇔ = ⇔ = ∈
ℤ
f x x x x k k
π
,
( ) ( )
2
4 sin 1 sin 1 2
2
= ⇔ = ⇔ = ± ⇔ = ± + ∈
ℤ
f x x x x k k
π
π
.
V
ậ
y giá tr
ị
nh
ỏ
nh
ấ
t c
ủ
a
(
)
f x
là 0
đạ
t
đượ
c khi
(
)
= ∈
ℤ
x k k
π
,
giá tr
ị
l
ớ
n nh
ấ
t c
ủ
a
(
)
f x
là 4
đạ
t
đượ
c khi
( )
2
2
= ± + ∈
ℤ
x k k
π
π
.
Cách 2: Đặ
t
2
sin
=
x t
,
Đ
i
ề
u ki
ệ
n
[
]
0;1
∈
t
2.
Đ
i
ề
u ki
ệ
n:
3
2
≤
≤
x
y
.
Ph
ươ
ng trình th
ứ
nh
ấ
t c
ủ
a h
ệ
t
ươ
ng
đươ
ng v
ớ
i:
(
)
(
)
(
)
(
)
(
)
3 3
2 3 2 1 3 1 1
− + − = − + −x x y y
y
2
y
1
+∞
-∞
++
_
0
0
+∞
-∞ m+1
m-1
y
y'
x
Đề thi chọn học sinh giỏi Toán 12 năm 2018 - 2019
VnDoc xin giới thiệu tới bạn đọc Đề thi chọn học sinh giỏi lớp 12 môn Toán cấp cơ sở năm 2018 - 2019 Sở GD&ĐT Điện Biên. Tài liệu gồm 5 câu hỏi bài tập, thời gian làm bài 180 phút, đề thi có đáp án. Mời các bạn học sinh tham khảo.
