Đề thi chọn học sinh giỏi lớp 9 môn Toán Phòng GD&ĐT huyện Lai Vung năm học 2018 - 2019
Đề thi chọn HSG lớp 9 môn Toán có đáp án
PHO
̀
NG GIA
́
O DU
̣
C VA
̀
ĐA
̀
O TA
̣
O
HUYỆN LAI VUNG
KỲ THI CHỌN HỌC SINH GIỎI LỚP 9
NĂM HO
̣
C 2018 – 2019
ĐỀ CHÍNH THỨC
MÔN THI: TOÁN
Thời gian làm bài: 150 phút
Ngày thi: 25/11/2018
Họ và tên thí sinh:.......................................... Số báo danh:...............................
Chữ ký của giám thị 1:...................... Chữ ký của giám thị 2:............................
NỘI DUNG ĐỀ THI
(Đề thi có 02 trang, gồm 5 câu)
Câu I (4,0 điểm)
1. Tính A =
( 8 3 2 2 5)( 2 10 0,2)
2. Tìm các số tự nhiên n sao cho B =
2
n +2n+18
là số chính phương.
3. Với a, b là các số nguyên. Chứng minh rằng nếu a chia cho 13 dư 2 và b
chia cho 13 dư 3 thì
2 2
a + b
chia hết cho 13.
Câu II (4,0 điểm)
1. Cho biểu thức C =
x x - 3 2( x - 3) x + 3
- +
x - 2 x - 3 x + 1 3 - x
. Tìm điều kiện xác
định và rút gọn biểu thức C.
2. a) Chứng minh
4 2
1
x + 1 (x + 4)
17
với mọi số thực x. Dấu đẳng
thức xảy ra khi nào?
b) Cho a, b là các số thực thỏa mãn
2 2
1
a + b
2
. Tìm giá trị nhỏ nhất của
biểu thức D =
4 4
a +1+ b +1
.
Câu III (4,0 điểm)
1. Giải các phương trình sau:
a)
4 3
x + 2x = 4x + 4
b)
2
1 1
+ x + 2 = + 2x + 1
x x
2. Giải bài toán sau bằng cách lập phương trình:
An dự định đi từ A đến B bằng xe đạp điện trong khoảng thời gian nhất
định. Nếu An đi với vận tốc 20 km/h thì đến B sớm 12 phút. Nếu An đi với vận
tốc 12 km/h thì đến B trễ 20 phút. Tính quãng đường AB và thời gian dự định đi
lúc đầu của An.
Câu IV (4,0 điểm)
1. Cho hình vuông ABCD và điểm M thuộc cạnh BC (M khác B, C). Một
đường thẳng đi qua A và vuông góc với AM cắt CD tại N.
a) Chứng minh BM = DN.
b) Tính tỉ số
AM
MN
.
2. Cho tam giác ABC, đường cao AH. Trên tia đối tia AH lấy điểm D sao cho
AD = BC. Tại B kẻ BE AB sao cho BE = AB (E và C thuộc hai nửa mặt
phẳng đối nhau từ bờ là AB). Tại C kẻ CF AC sao cho CF = AC (F và B thuộc
hai nửa mặt phẳng đối nhau từ bờ là AC). Chứng minh rằng ba đường thẳng DH,
BF và CE đồng quy.
Câu V (4,0 điểm)
Cho đường tròn (O ; R) và một điểm A ở ngoài đường tròn. Từ một điểm
M di động trên đường thẳng d vuông góc với OA tại A, vẽ các tiếp tuyến ME,
MF với đường tròn (O) (E, F là các tiếp điểm). Đường thẳng chứa đường kính
của đường tròn song song với EF cắt ME, MF lần lượt tại C và D. Dây EF cắt
OM tại H, cắt OA tại B.
1. Chứng minh rằng: OA.OB không đổi.
2. Chứng minh EF luôn đi qua một điểm cố định khi M di chuyển trên đường
thẳng d.
3. Tìm vị trí của M trên đường thẳng d để diện tích của HBO lớn nhất.
--- HẾT ---
Lưu ý: Thí sinh không được sử dụng tài liệu. Giám thị không giải thích gì thêm.
PHO
̀
NG GIA
́
O DU
̣
C VA
̀
ĐA
̀
O TA
̣
O
HUYỆN LAI VUNG
Hướng dẫn chấm gồm 04 trang
HƯỚNG DẪN CHẤM VÀ THANG ĐIỂM
KỲ THI CHỌN HỌC SINH GIỎI LỚP 9
NĂM HO
̣
C 2018 – 2019
MÔN: TOÁN
I. HƯỚNG DẪN CHUNG:
1. Học sinh làm bài không theo cách nêu trong hướng dẫn chấm nhưng
đúng, chính xác, chặt chẽ thì cho đủ số điểm của câu đó.
2. Việc chi tiết hóa (nếu có) thang điểm trong hướng dẫn chấm phải đảm
bảo không làm sai lệch hướng dẫn chấm và phải được thống nhất thực hiện
trong tổ chấm thi.
3. Điểm toàn bài tính theo thang điểm 20, làm tròn số đến 0,25 điểm.
II. ĐÁP ÁN VÀ THANG ĐIỂM
Nội dung
Điểm
Câu I
4,0
1. Tính A=
( 8 3 2 2 5)( 2 10 0,2)
1,0
A ( 8 3 2 2 5)( 2 10 0,2)
(2 2 3 2 2 5)( 2 20)
0,25
(2 5 2)(2 5 2)
0,25
2 2
(2 5) ( 2)
0,25
= 20 - 2 = 18 0,25
2. Tìm các số tự nhiên n sao cho B =
2
2 18n n
là số chính phương.
1,5
Đặt
2 2
2 18n n a
(
a
,
n
)
0,25
2 2
(n 1) 17
a
0,25
(a n 1)( n 1) 17a
0,25
Vì
a
,
n
nên
(a n 1) ( n 1)a
; 17 là số nguyên tố.
0,25
Suy ra:
a n 1 17
(*)
và
a n 1 1
hay
a n 2
0,25
Thay
a n 2
vào (*) tính được n = 7 0,25
3. Với a, b là các số nguyên. Chứng minh rằng nếu a chia cho 13 dư 2
và b chia cho 13 dư 3 thì
2 2
a +b
chia hết cho 13.
1,5
Do: a chia cho 13 dư 2 nên
a=13x+2
(
x
) 0,25
b chia cho 13 dư 3 nên
b=13y+3
(
y
)
0,25
Suy ra:
2 2
a +b
=
2 2
(13x+2) +(13y+3)
0,25
=
2 2
169x +52x+4+169y +78y+9
0,25
=
2 2
13(13x +4x+13y +6y+1) 13.K 13
0,25
Vậy:
2 2
a +b
chia hết cho 13 (đpcm)
0,25
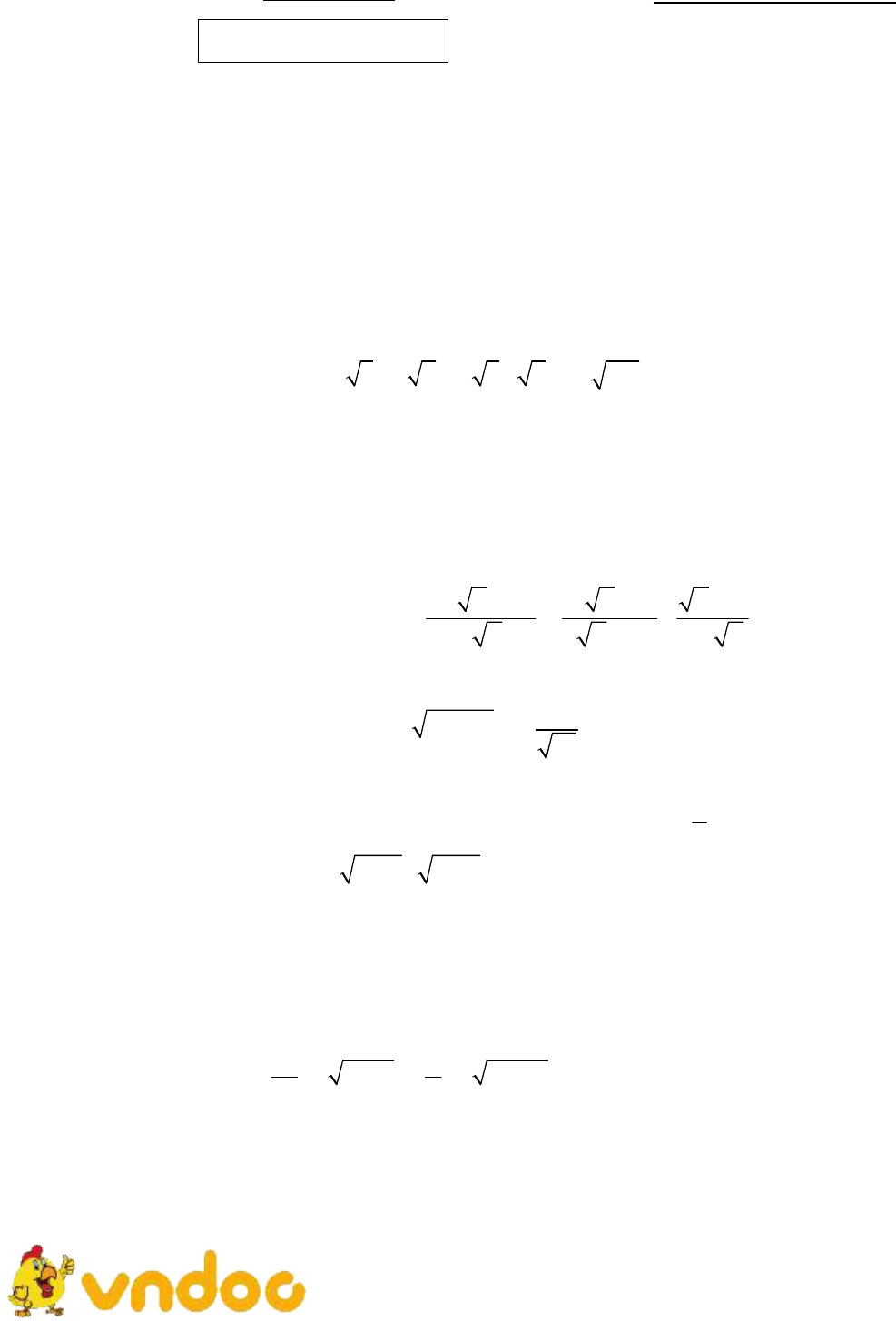
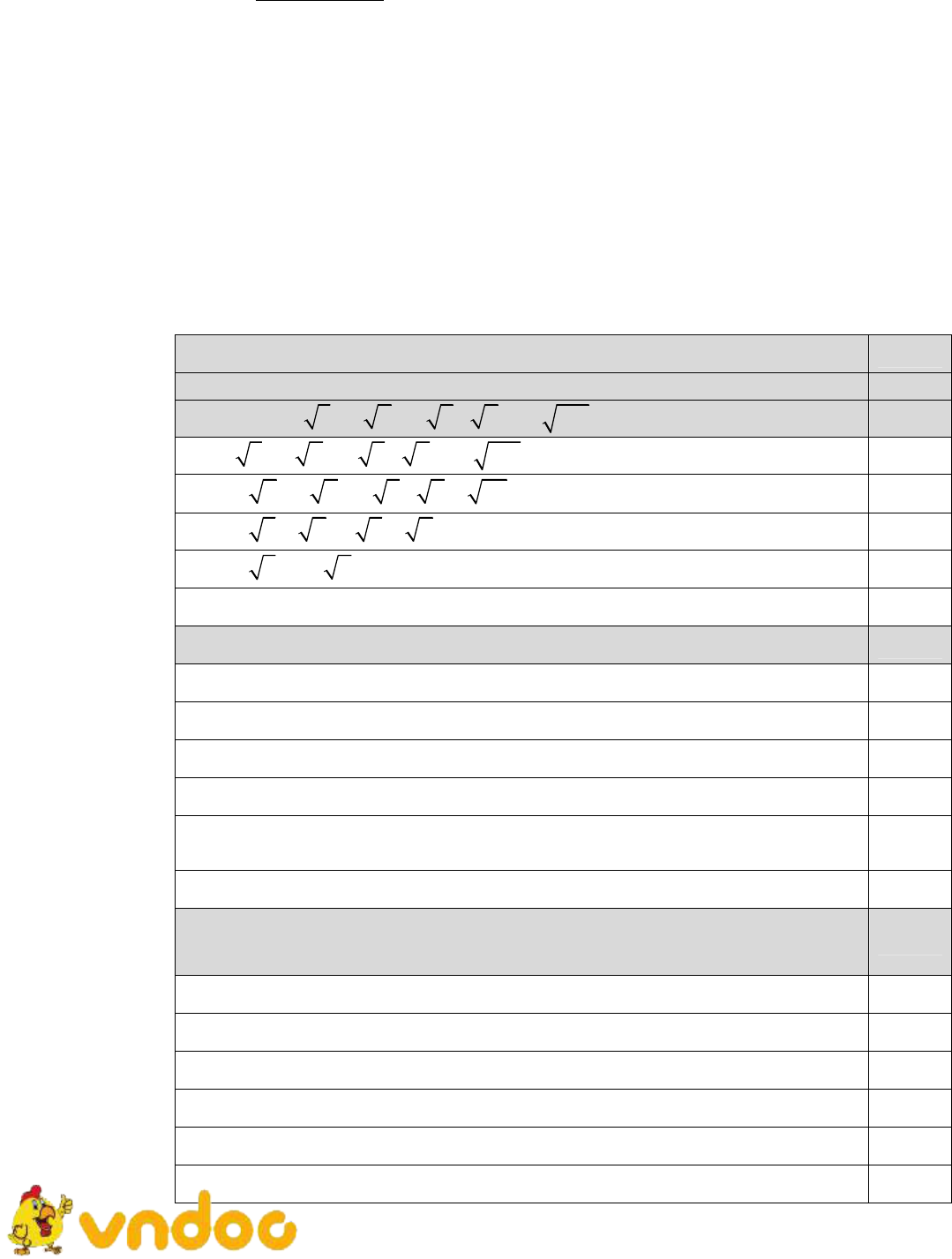
Đề thi chọn học sinh giỏi lớp 9 môn Toán huyện Lai Vung năm 2018
Đề thi chọn học sinh giỏi lớp 9 môn Toán Phòng GD&ĐT huyện Lai Vung năm học 2018 - 2019 là đề tham khảo dành cho các bạn học sinh và thầy cô nghiên cứu, học tập tốt môn Toán lớp 9 cũng như luyện tập và làm quen với nhiều đề học sinh giỏi hơn nhằm chuẩn bị tốt nhất cho các kì thi sắp diễn ra. Mời các bạn tham khảo.
............................................
Nhằm đáp ứng nhu cầu của các bạn học sinh lớp 9 tìm kiếm tài liệu ôn thi học kì I, chúng tôi xin giới thiệu một số đề thi học kì 1 lớp 9 năm 2018 tải nhiều nhất. Mời các bạn cùng tham khảo tài liệu dưới đây
- Đề thi chọn học sinh giỏi cấp thành phố lớp 9 môn Ngữ văn Phòng GD&ĐT Hà Nội năm học 2018 - 2019
- Đề thi chọn học sinh giỏi cấp thành phố lớp 9 môn Toán Phòng GD&ĐT Hà Nội năm học 2018 - 2019
- Đề thi học kì 1 lớp 9 môn Toán Phòng GD&ĐT Quận Bắc Từ Liêm năm học 2018 - 2019
- Đề thi học kì 1 lớp 9 môn Ngữ văn Phòng GD&ĐT Dĩ An năm học 2018 - 2019
Mời các bạn tham khảo tài liệu sau: Toán lớp 9, Giải bài tập Toán lớp 9, Tài liệu học tập lớp 9, Đề thi giữa kì 1 lớp 9, Đề thi học kì 1 lớp 9
