Đề thi giữa học kì 1 môn Toán lớp 11 trường THPT Đa Phúc, Hà Nội năm học 2016 - 2017

Đề thi giữa học kì 1 môn Toán lớp 11

Đề thi giữa học kì 1 môn Toán lớp 11 trường THPT Đa Phúc, Hà Nội năm học 2016 - 2017 là tài liệu tham khảo hay được Vndoc.com sưu tầm, dành cho quý thầy cô cùng các bạn học sinh lớp 11, nhằm ôn tập và củng cố kiến thức để chuẩn bị cho kì thi học kì 1 sắp tới. Hi vọng rằng với tài liệu này các bạn học sinh sẽ đạt được kết quả cao. Mời các bạn tham khảo.

Đề thi giữa học kì 1 môn Toán lớp 11 trường THPT Triệu Sơn 2, Thanh Hóa năm học 2016 - 2017

Đề thi giữa học kì 1 môn Toán lớp 11 trường THPT Trần Hưng Đạo, TP. Hồ Chí Minh năm học 2016 - 2017

Bộ đề kiểm tra giữa học kì 1 môn Toán lớp 11 năm học 2014 - 2015

Câu 1: (3,0 điểm). Từ các chữ số 1, 2, 3, 4, 5, 6 có thể lập được bao nhiêu số tự nhiên:

a) Có 4 chữ số.

b) Có 5 chữ số khác nhau trong đó nhất thiết phải có mặt chữ số 3 và chữ số 5.

Câu 2: (2,0 điểm). Tìm n ∈ N* thỏa mãn:

Câu 3: (2,0 điểm). Tìm số hạng không chứa x trong khai triển .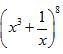

Câu 4: (2,0 điểm). Trên giá sách có 5 quyển sách Văn, 4 quyển sách Lịch sử và 3 quyển sách Địa lí. Lấy ngẫu nhiên 3 quyển sách. Tính xác suất sao cho:

a) Ba quyển sách lấy ra thuộc 3 môn khác nhau.

b) Ít nhất lấy được một quyển sách Văn.

Câu 5: (1,0 điểm). Số 680 400 có bao nhiêu ước số tự nhiên?

Đáp án đề thi giữa học kì 1 môn Toán lớp 11

Câu 1 (3 điểm)

a) Gọi số cần lập dạng . Chọn liên tiếp các bước sau:

Chọn a có 6 cách.

Chọn b có 6 cách.

Chọn c có 6 cách.

Chọn d có 6 cách.

Theo quy tắc nhân có 6⁴ = 1296 số lập được.

b) Xếp chữ số 3 và chữ số 5 vào 2 trong 5 vị trí có cách.

Tiếp theo, lấy 3 trong 4 chữ số còn lại xếp vào 3 vị trí còn lại có cách.

Suy ra có A²₅.A³₄ = 480 số thỏa mãn bài toán.

Câu 2 (2 điểm)

Điều kiện: n ≥ 3, n ∈ N

Có phương trình ẩn n dạng:

So sánh điều kiện có n = 9 thỏa mãn

Câu 3 (2 điểm)

Xét trong khai triển 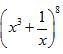có số hạng tổng quát là:

với 0 ≤ k ≤ 8, k ∈ N.

Số hạng không chứa x ứng với 24 - 4k = 0 → k = 6

Vậy số hạng đó là C⁶₈ = 28

Câu 4 (2 điểm)

a) Tổng số có 12 quyển sách, lấy 3 quyển suy ra số phần tử của không gian mẫu là: n(Ω) = C³₁₂ = 220

Gọi A là biến cố "Ba quyển lấy ra thuộc 3 môn khác nhau"

Để có 1 phần tử của A ta phải tiến hành lần lượt 3 lựa chọn từ mỗi loại sách 1 quyển → n(A) = 5.4.3 = 60.

Vậy xác suất của biến cố A là:

b) Gọi B là biến cố: "Ít nhất lấy được một quyển sách Văn"

là biến cố "trong 3 quyển sách lấy ra không có quyển sách Văn nào"

Lại có tổng số quyển sách Lịch sử và Địa lí là 7.

Suy ra:

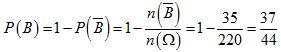
Câu 5 (1 điểm)

Có 680400 = 2⁴.3⁵.5².7

Một ước tự nhiên của 680400 có dạng 2^a.3^b.5^c.7^d

Trong đó a, b, c, d ∈ N; 0 ≤ a ≤ 4; 0 ≤ b ≤ 5; 0 ≤ c ≤ 2; 0 ≤ d ≤ 1.

Để chọn được một ước số đó ta thực hiện liên tiếp các bước:

Chọn a có 5 cách

Chọn b có 6 cách

Chọn c có 3 cách

Chọn d có 2 cách

Theo quy tắc nhân có 5.6.3.2 = 180 ước số tìm được

Kết luận: 680400 có 180 ước số tự nhiên.