Đề thi học kì 2 Toán 10 CTST (Cấu trúc mới) năm 2025 Đề 1

Đề thi học kì 2 môn Toán 10 Chân trời sáng tạo

Đề thi học kì 2 lớp 10 môn Toán CTST năm 2025 được VnDoc biên soạn được đưa ra dựa vào ma trận đề kiểm tra theo Công văn 7991 của Bộ Giáo dục và Đào tạo, áp dụng bắt đầu từ học kì 2 đối với THPT. Mời các bạn tham khảo chi tiết nội dung trong file tải về.

Đề thi cuối học kì 2 lớp 10 gồm có 4 phần:

• Phần 1: Trắc nghiệm khách quan
• Phần 2: Trắc nghiệm đúng sai
• Phần 3: Câu hỏi tự luận ngắn
• Phần 4: Tự luận.

Hy vọng thông qua nội dung tài liệu, sẽ giúp bạn học ôn tập, củng cố kiến thức, chuẩn bị tốt cho bài kiểm tra đánh giá học kì 2 môn Toán lớp 10.

Trường THPT Chân trời sáng tạo Đề thi thử số 1

ĐỀ KIỂM TRA CUỐI HỌC KỲ II MÔN: TOÁN - LỚP 10 NĂM HỌC: 2024 – 2025 Thời gian làm bài: 90 phút

Họ và tên học sinh: …………………………….. Lớp: …………………………..

PHẦN I. PHẦN TRẮC NGHIỆM KHÁCH QUAN NHIỀU LỰA CHỌN

Thí sinh trả lời từ câu 1 đến câu 20. Mỗi câu hỏi thí sinh chỉ chọn 1 phương án.

Câu 1: Gieo một đồng tiền và một con súc sắc cân đối đồng chất. Số phần tử của không gian mẫu trong phép thử trên là

A. \(12\).                               B. \(36\).                             C. \(4\).                        D. \(8\).

Câu 2: Từ bốn chữ số \(1,2,3,4\) có thể lập được bao nhiêu số tự nhiên gồm ba chữ số?

A. \(12\).                            B. \(6\).                             C. \(64\).                           D. \(24\).

Câu 3: Một hộp có 5 quả cầu trắng, 4 quả cầu màu vàng và 6 quả cầu màu xanh. Lấy ngẫu nhiên 3 quả cầu. Tính xác suất để trong 3 quả lấy được có không quá hai màu.

A. \(\frac{369}{455}\).                          B. \(\frac{67}{91}\).                         C. \(\frac{24}{91}\).                           D. \(\frac{219}{255}\).

Câu 4: Tập nghiệm của bất phương trình \(x^{2} - 4x + 3 > 0\) là

A. \(S = ( - \infty;1) \cup \lbrack 3; + \infty)\).                           B. \(S = (1;3)\).

C. \(S = ( - \infty;1) \cup (3; + \infty)\).                           D. \(\lbrack 1;3\rbrack\).

Câu 5: Một lớp có 30 học sinh gồm 20 nam và 10 nữ. Hỏi có bao nhiêu cách chọn ra một nhóm 3 học sinh sao cho nhóm đó có một học sinh nữ?

A. 900.                       B. 2920.                   C. 1900.                  D. 1140.

Câu 6: Trong mặt phẳng tọa độ Oxy, cho hypebol có phương trình \(\frac{x^{2}}{15} - \frac{y^{2}}{10} = 1\). Tiêu cự hypebol bằng

A. 5.                               B. 6.                           C. 10.                     D. \(2\sqrt{5}\).

Câu 7: Một tổ có \(6\) học sinh nam và \(9\) học sinh nữ. Hỏi có bao nhiêu cách chọn \(6\) học sinh đi lao động, trong đó có đúng \(2\) học sinh nam?

A. \(C_{6}^{2} + C_{9}^{4}.\)                  B. \(C_{6}^{2}.C_{9}^{4}.\)                 C. \(A_{6}^{2}.A_{9}^{4}.\)                       D. \(C_{9}^{2}.C_{6}^{4}.\)

Câu 8: Viết khai triển theo công thức nhị thức Niu-tơn \(\left( x^{2} - y \right)^{5}\).

A. \(x^{10} - 5x^{8}y + 10x^{6}y^{2} - 10x^{4}y^{3} + 5x^{2}y^{4} - y^{5}\).

B. \(x^{10} - 5x^{8}y - 10x^{6}y^{2} - 10x^{4}y^{3} - 5x^{2}y^{4} + y^{5}\).

C. \(x^{10} + 5x^{8}y + 10x^{6}y^{2} + 10x^{4}y^{3} + 5x^{2}y^{4} + y^{5}\).

D. \(x^{10} + 5x^{8}y - 10x^{6}y^{2} + 10x^{4}y^{3} - 5x^{2}y^{4} + y^{5}\).

Câu 9: Từ một hộp chứa \(15\) quả cầu gồm \(10\) quả màu đỏ và \(5\) quả màu xanh, lấy ngẫu nhiên đồng thời hai quả. Xác suất để lấy được hai quả có màu khác nhau là

A. \(\frac{10}{21}\).                    B. \(\frac{2}{21}\).                           C. \(\frac{1}{7}\).                     D. \(\frac{3}{7}\).

Câu 10: Trong mặt phẳng \(Oxy\)cho elip có phương trình \((E):\frac{x^{2}}{25} + \frac{y^{2}}{9} = 1\). Đường thẳng \(\Delta:x = - 4\) cắt elip \((E)\) tại hai điểm \(M,N\). Tính độ dài đoạn thẳng \(MN\)?

A. \(MN = \frac{9}{25}\).                      B. \(MN = \frac{18}{5}\).                 C. \(MN = \frac{9}{5}\).             D. \(MN = \frac{18}{25}\).

Câu 11: Cho parabol có phương trình: \(4y^{2} = 20x\). Phương trình đường chuẩn của parabol là:

A. \(x = \frac{5}{4}\).                B. \(x = \frac{4}{5}\).                   C. \(x = - \frac{4}{5}\).                   D. \(x = - \frac{5}{4}\).

Câu 12: Trong mặt phẳng với hệ tọa độ \(Oxy\), cho hai đường thẳng \(d_{1}:5x + 3y - 3 = 0\) và \(d_{2}:5x + 3y + 7 = 0\) song song nhau. Đường thẳng vừa song song và cách đều với \(d_{1},\ d_{2}\) là:

A. \(5x + 3y - 2 = 0.\)                        B. \(5x + 3y + 4 = 0.\)

C. \(5x + 3y + 2 = 0.\)                      D. \(5x + 3y - 4 = 0.\)

PHẦN II. CÂU TRẮC NGHIỆM ĐÚNG SAI

Thí sinh trả lời từ câu 1 đến câu 2. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.

Câu 1: Cho tập hợp \(A = \left\{ 1;2;3;4;5 \right\}\)

a) Từ tập A lập được 25 số có hai chữ số.

b) Từ tập A lập được 101 số lẻ có ba chữ số khác nhau.

c) Từ tập A lập được 24 số chẵn có ba chữ số khác nhau.

d) Từ tập A lập được 125 số có ba chữ số có ba chữ số khác nhau.

Câu 2: Trong không gian \(Oxy\), cho đường tròn \((C):(x - 1)^{2} + (y - 4)^{2} = 4\)

a) Điểm \(A(3;4)\)nằm trên đường tròn \((C)\)

b) Phương trình đường tròn \((C)\)có thể viết dưới dạng: \(x^{2} + y^{2} - 2x - 8y + 13 = 0\)

c) Phương trình tiếp tuyến với đường tròn \((C)\)song song với đường thẳng \((\Delta):4x - 3y - 2 = 0\) là \(4x - 3y + 18 = 0\) và \(4x - 3y - 2 = 0\)

d) Đường tròn \((C)\)có tâm \(I(1;2)\) bán kính \(R = 2\)

PHẦN III. CÂU TRẮC NGHIỆM TRẢ LỜI NGẮN

Thí sinh trả lời từ câu 1 đến câu 4.

Câu 1: Tìm số hạng không chứa \(x\) trong khai triển \(\left( x + \frac{1}{2x} \right)^{4}\).

Câu 2: Một lớp học có \(30\) học sinh gồm có cả nam và nữ. Chọn ngẫu nhiên \(3\) học sinh để tham gia hoạt động của Đoàn trường. Xác suất chọn được \(2\) nam và \(1\) nữ là \(\frac{12}{29}\). Tính số học sinh nữ của lớp.

Câu 3: Trong mặt phẳng tọa độ \(Oxy\), cho đường thẳng \(d:4x + 2y + 1 = 0\) và điểm \(A(1;1)\). Gọi \(H(a;b)\) là hình chiếu vuông góc của \(A\) lên \(d\). Tính \(a + b\).

Câu 4: Một mảnh đất hình Elip có độ dài trục lớn bằng \(120m\), độ dài trục bé bằng \(90m\).

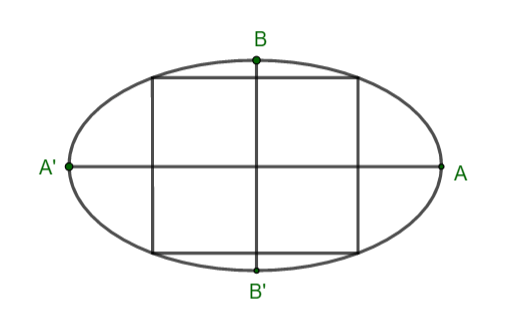
Tập đoàn Vingroup dự định xây dựng một trung tâm thương mại Vincom trong một hình chữ nhật nội tiếp của Elip như hình vẽ. Hỏi diện tích xây dựng Vincom lớn nhất là bao nhiêu mét vuông?

PHẦN IV. TỰ LUẬN

Câu 1: Cho đường thẳng \(d:\ - 3x + y - 5 = 0\) và điểm \(M( - 2;1)\). Tọa độ hình chiếu vuông góc của \(M\)trên \(d\) là

Câu 2: Trong mặt phẳng \(Oxy\), cho elip \((E)\) có một tiêu điểm là \(F_{1}\left( - \sqrt{3}\ ;0 \right)\) và đi qua điểm \(M\left( - \sqrt{3}\ ;\frac{1}{2} \right)\). Viết phương trình chính tắc của elip \((E)\)

Câu 3: Từ 1 bó gồm 5 bông hoa đỏ, 6 bông hoa vàng, 7 bông hoa tím. Có bao nhiêu cách chọn 4 bông hoa có đủ cả 3 màu.

Câu 4: Trong một hộp có \(10\) viên bi đánh số từ \(1\) đến \(10\), lấy ngẫu nhiên ra hai bi. Tính xác suất để hai bi lấy ra có tích hai số trên chúng là một số lẻ.

Câu 5: Chi đoàn lớp \(12A\) có \(20\) đoàn viên trong đó có \(12\) đoàn viên nam và \(8\) đoàn viên nữ. Tính xác suất khi chọn \(3\) đoàn viên có ít nhất \(1\) đoàn viên nữ.

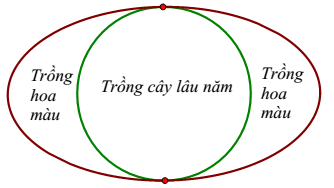
Câu 6: Ông Hoàng có một mảnh vườn hình Elip có chiều dài trục lớn và trục nhỏ lần lượt là \(60m\) và \(30m\). Ông chia mảnh vườn ra làm hai nửa bằng một đường tròn tiếp xúc trong với Elip để làm mục đích sử dụng khác nhau (xem hình vẽ). Nửa bên trong đường tròn ông trồng cây lâu năm, nửa bên ngoài đường tròn ông trồng hoa màu. Tính tỉ số diện tích T giữa phần trồng cây lâu năm so với diện tích trồng hoa màu. Biết diện tích hình Elip được tính theo công thức \(S = \pi ab\), với a, b lần lượt là nửa độ dài trục lớn và nửa độ dài trục nhỏ. Biết độ rộng của đường Elip là không đáng kể.

---------- HẾT ----------

------------------------------------------

Đáp án chi tiết có trong file tải