Đề thi thử vào lớp 10 môn Toán chuyên Toán - Tin lần 2 năm học 2015-2016 trường THPT Chuyên Nguyễn Huệ, Hà Nội
Đề thi thử vào lớp 10 môn Toán chuyên Toán - Tin lần 2 năm học 2015-2016 trường THPT Chuyên Nguyễn Huệ, Hà Nội là đề thi thử vào lớp 10 môn Toán đáp án hay và chất lượng, giúp các bạn ôn tập cũng như làm quen với nhiều dạng đề và câu hỏi, là tài liệu ôn thi vào lớp 10 rất tốt, nhất là với các bạn đang ôn thi vào lớp 10 THPT Chuyên.
Đề thi thử vào lớp 10 môn Toán
| TRƯỜNG THPT CHUYÊN NGUYỄN HUỆ | KỲ THI THỬ VÀO LỚP 10 CHUYÊN THPT LẦN THỨ HAI NĂM HỌC 2015 - 2016 Môn thi: TOÁN Thời gian làm bài: 150 phút (dùng cho thí sinh thi vào lớp chuyên Toán và chuyên Tin) |
Bài I (3 điểm)
1) Chứng minh rằng với mọi số tự nhiên n thì n4 + 2015n² chia hết cho 12
2) Giải hệ phương trình sau :
| { | 2x² + 3xy + y² = 12 |
| x² - xy + 3y² = 11 |
Bài II (2 điểm)
1) Tìm tất cả các cặp số nguyên (x, y) thỏa mãn: 2y² + 2xy + x + 3y - 13 = 0.
2) Giải phương trình:
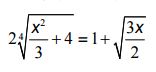
Bài III (1 điểm)
Cho x y, là các số thực không âm. Tìm giá trị lớn nhất của biểu thức:
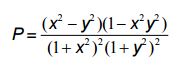
Bài IV (3 điểm)
Cho hai đường tròn (O) và (O’) cắt nhau tại A và B. Kẻ tiếp tuyến chung CD (C, D là tiếp điểm, C thuộc (O), D thuộc (O’)). Đường thẳng qua A song song với CD cắt (O) tại E, (O’) tại F. Gọi M, N theo thứ tự là giao điểm của BD và BC với EF. Gọi I là giao điểm của EC với FD.
Chứng minh rằng:
a) Chứng minh rằng tứ giác BCID nội tiếp.
b) CD là trung trực của đoạn thẳng AI.
b) IA là phân giác góc MIN.
Bài V (1điểm)
Cho 1010 số tự nhiên phân biệt không vượt quá 2015 trong đó không có số nào gấp 2 lần số khác. Chứng minh rằng trong các số được chọn luôn tìm được 3 số sao cho tổng của 2 số bằng số còn lại.
------------------------- Hết----------------------
(Giám thị không giải thích gì thêm)
Họ và tên thí sinh: .....................................................Số báo danh:...............................
Chữ ký của giám thị số 1: Chữ ký của giám thị số 2:
Đáp án đề thi thử vào lớp 10 môn Toán
Bài I:
1) Chứng minh rằng với mọi số tự nhiên n thì n4 + 2015n² chia hết cho 12.
Ta có: n4 + 2015n² = n²(n² + 2015)
- Nếu n chẵn thì n² chia hết cho 4.
- Nếu n lẻ thì n2 + 2015 chia hết cho 4.
Suy ra n4 + 2015n² chia hết cho 4.
Nếu n chia hết cho 3 thì n4 + 2015n² chia hết cho 3
Nếu n chia 3 dư 1 hoặc dư 2 thì n4 + 2015n² chia hết cho 3. Vậy n4 + 2015n² chia hết cho 3. Vì (4, 3) = 1 nên n4 + 2015n² chia hết cho 12.



