Đề thi tuyển sinh vào lớp 10 môn Toán sở GD&ĐT Bình Thuận năm 2015 - 2016
Đề thi tuyển sinh vào lớp 10 môn Toán
Đề thi tuyển sinh lớp 10 THPT môn Toán của sở GD&ĐT Bình Thuận năm 2015 - 2016 được VnDoc.com sưu tầm và đăng tải là tài liệu tham khảo hữu ích dành cho các bạn học sinh lớp 9, giúp các bạn ôn tập và nâng cao kiến thức môn Toán, chuẩn bị cho kì thi tuyển sinh vào lớp 10 hiệu quả. Đề thi có đáp án, mời các bạn tham khảo.
Đề thi tuyển sinh lớp 10 THPT môn Toán sở GD&ĐT Hải Dương năm 2015 - 2016
Đề thi tuyển sinh vào lớp 10 môn Ngữ văn sở GD&ĐT Tây Ninh năm 2015 - 2016
| SỞ GIÁO DỤC VÀ ĐÀO TẠO BÌNH THUẬN |
KỲ THI TUYỂN SINH VÀO LỚP 10 THPT Năm học: 2015 – 2016 Môn thi: TOÁN Thời gian làm bài: 120 phút (Không kể thời gian phát đề) |
Bài 1: (2 điểm) Giải phương trình và hệ phương trình sau:
a) x2 + x - 6 = 0
![]()
Bài 2: (2 điểm) Rút gọn biểu thức: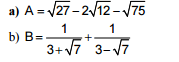
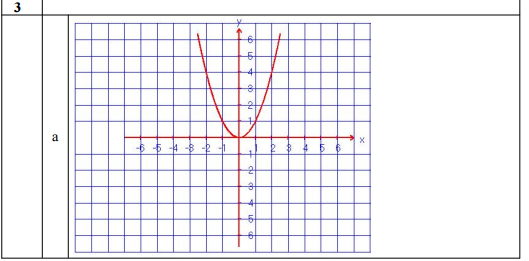
Bài 3: (2 điểm)
a) Vẽ đồ thị ( P) của hàm số y = x2
b) Chứng minh rằng đường thẳng (d): y = kx + 1 luôn cắt đồ thị (P) tại hai điểm phân biệt với mọi k .
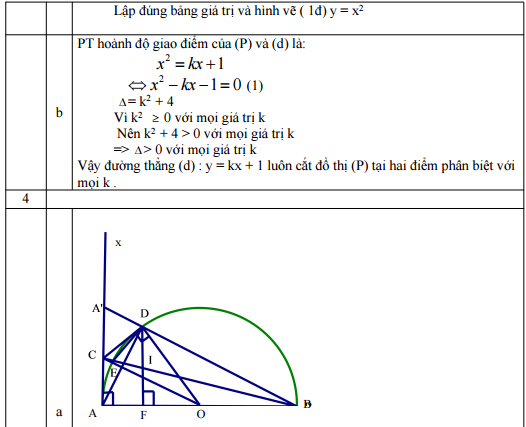
Bài 4: (4 điểm)
Cho nửa đường tròn tâm O đường kính AB = 2R, D là một điểm tùy ý trên nửa đường tròn (D khác A và D khác B) . Các tiếp tuyến với nửa đường tròn (O) tại A và D cắt nhau tại C, BC cắt nửa đường tròn (O) tại điểm thứ hai là E. Kẻ DF vuông góc với AB tại F.
a) Chứng minh: Tứ giác OACD nội tiếp.
b) Chứng minh: CD2 = CE.CB
c) Chứng minh: Đường thẳng BC đi qua trung điểm của DF.
d) Giả sử OC = 2R, tính diện tích phần tam giác ACD nằm ngoài nửa đường tròn (O) theo R.
Đáp án đề thi tuyển sinh vào lớp 10 môn Toán