Đề thi tuyển sinh lớp 10 THPT môn Toán sở GD&ĐT Hải Dương năm 2015 - 2016

Đề thi tuyển sinh lớp 10 THPT môn Toán

Đề thi tuyển sinh lớp 10 THPT môn Toán của sở GD&ĐT Hải Dương năm 2015 - 2016 được VnDoc.com sưu tầm và đăng tải là tài liệu tham khảo hữu ích dành cho các bạn học sinh lớp 9, giúp các bạn ôn tập và nâng cao kiến thức môn Toán, chuẩn bị cho kì thi tuyển sinh vào lớp 10 hiệu quả. Đề thi có đáp án, mời các bạn tham khảo.

Đề thi tuyển sinh lớp 10 THPT Chuyên Long An năm học 2014 - 2015 môn Ngữ văn (chuyên)

Đề thi tuyển sinh lớp 10 môn Toán (chung) năm 2015 - 2016 trường THPT Chuyên Khoa học Tự nhiên, Hà Nội

Câu I (2,0 điểm) Giải các phương trình và hệ phương trình sau:

1) 2x + 1 = 0

3) x⁴ + 8x² - 9 = 0

Câu II (2,0 điểm)

1) Rút gọn biểu thức với a ≥ 0

2) Khoảng cách giữa hai tỉnh A và B là 60km. Hai người đi xe đạp cùng khởi hành một lúc đi từ A đến B với vận tốc bằng nhau. Sau khi đi được 1 giờ thì xe của người thứ nhất bị hỏng nên phải dừng lại sửa xe 20 phút, còn người thứ hai tiếp tục đi với vận tốc ban đầu. Sau khi xe sửa xong, người thứ nhất đi với vận tốc nhanh hơn trước 4km/h nên đã đến B cùng lúc với người thứ hai. Tính vận tốc hai người đi lúc đầu.

Câu III (2,0 điểm)

1) Tìm các giá trị của m để phương trình x² - 2(m + 1)x + m² - 3 = 0 có nghiệm kép. Tìm nghiệm kép đó.

2) Cho hai hàm số y = (3m + 2)x + 5 với m ≠ -1 và y = -x -1 với và có đồ thị cắt nhau tại điểm A (x; y). Tìm các giá trị của m để biểu thức P = y² + 2x -3 đạt giá trị nhỏ nhất.

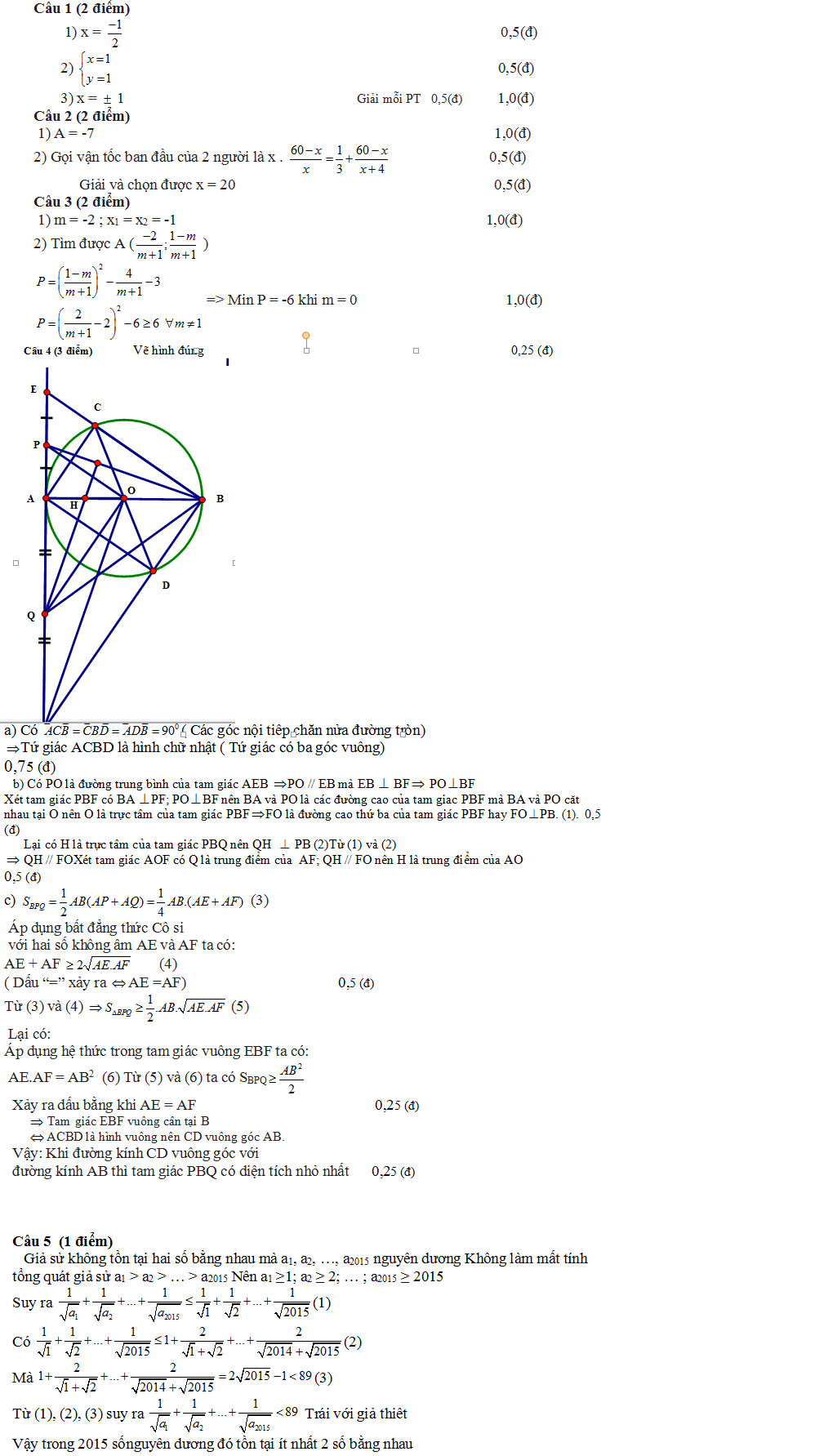
Câu IV (3,0 điểm)

Cho đường tròn (O) đường kính AB cố định và đường kính CD thay đổi không trùng với AB. Tiếp tuyến tại A của đường tròn (O) cắt các đường thẳng BC và BD lần lượt tại E và F. Gọi P và Q lần lượt là trung điểm của các đoạn thẳng AE và AF.

1) Chứng minh ACBD là hình chữ nhật;

2) Gọi H là trực tâm của tam giác BPQ. Chứng minh H là trung điểm của OA;

3) Xác định vị trí của đường kính CD để tam giác BPQ có diện tích nhỏ nhất.

Câu V (1,0 điểm) Cho 2015 số nguyên dương a₁; a₂; a₃;....; a₂₀₁₅ thỏa mãn điều kiện:

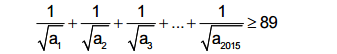
Chứng minh rằng trong 2015 số nguyên dương đó, luôn tồn tại ít nhất 2 số bằng nhau.

Đáp án đề thi tuyển sinh lớp 10 THPT môn Toán