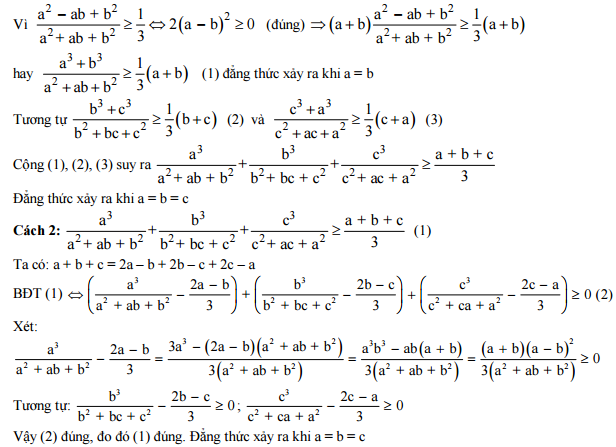Đề thi tuyển sinh vào lớp 10 THPT chuyên môn Toán trường THPT chuyên Lê Qúy Đôn, Bình Định năm 2015 - 2016
Đề thi tuyển sinh vào lớp 10 THPT chuyên môn Toán
Đề thi tuyển sinh vào lớp 10 THPT chuyên môn Toán trường THPT chuyên Lê Qúy Đôn, Bình Định năm 2015 - 2016 được VnDoc.com sưu tầm và đăng tải là tài liệu tham khảo hữu ích dành cho các bạn học sinh lớp 9, giúp các bạn ôn tập và nâng cao kiến thức môn Toán, chuẩn bị cho kì thi tuyển sinh vào lớp 10 hiệu quả. Đề thi có đáp án, mời các bạn tham khảo.
Đề thi tuyển sinh vào lớp 10 THPT môn Ngữ văn tỉnh Bắc Giang năm 2015 - 2016
Đề thi tuyển sinh vào lớp 10 THPT môn Toán tỉnh Bắc Giang năm 2015 - 2016
|
SỞ GIÁO DỤC VÀ ĐÀO TẠO BÌNH ĐỊNH |
KỲ THI TUYỂN SINH VÀO LỚP 10 THPT CHUYÊN |
Bài 1: (2 điểm)
a) Cho số thực x > 0 thỏa mãn điều kiện:![]()
Tính giá trị các biểu thức ![]()
b) Rút gọn biểu thức ![]()
Bài 2: (2 điểm)
a) Tìm các số nguyên x, y, z thỏa mãn: x2 + 5y2 + z2 + 2(y - z) < 4xy - 1
b) Giải hệ phương trình:
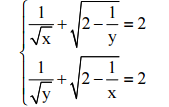
Bài 3: (2 điểm)
a) Chứng minh phân số![]() là tối giản với mọi n nguyên dương.
là tối giản với mọi n nguyên dương.
b) Giải phương trình x2 - mx + n = 0, biết rằng phương trình có hai nghiệm nguyên dương phân biệt và m, n là hai số nguyên tố.
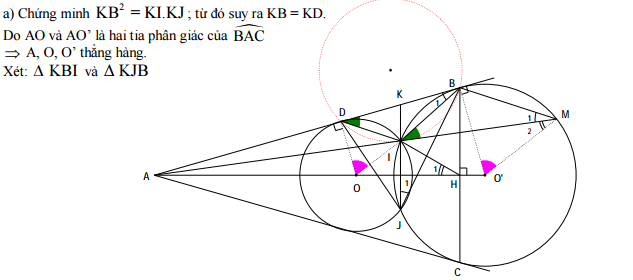
Bài 4: (3 điểm) Cho hai đường tròn (O; R) và (O'; R') cắt nhau tại I và J (R' > R). Kẻ các tiếp tuyến chung của hai đường tròn đó; chúng cắt nhau ở A. Gọi B và C là các tiếp điểm của hai tiếp tuyến trên với (O'; R'); D là tiếp điểm của tiếp tuyến AB với (O; R) (điểm I và điểm B ở cùng nửa mặt phẳng bờ là O'A). Đường thẳng AI cắt (O'; R') tại M (điểm M khác điểm I).
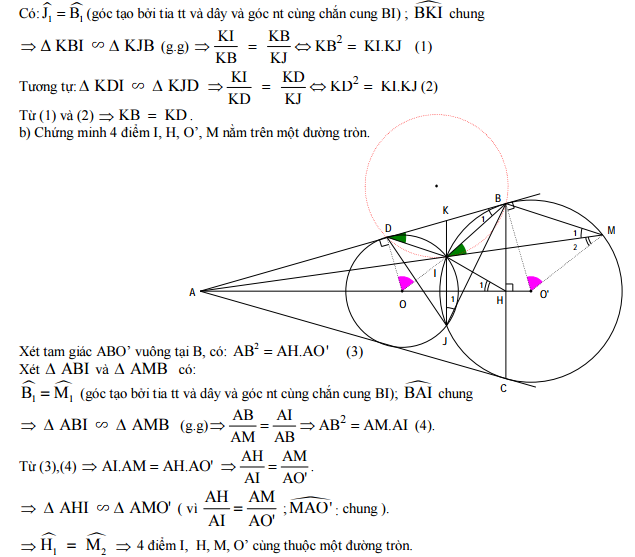
a) Gọi K là giao điểm của đường thẳng IJ với BD. Chứng minh KB2 = KI.KJ; từ đó suy ra KB = KD.
b) AO' cắt BC tại H. Chứng minh 4 điểm I, H, O', M nằm trên một đường tròn.
c) Chứng minh đường thẳng AM là tiếp tuyến của đường tròn ngoại tiếp Δ IBD
Bài 5: (1 điểm) Cho a, b, c > 0. Chứng minh rằng
![]()
Đáp án đề thi tuyển sinh vào lớp 10 THPT chuyên môn Toán
Bài 1:
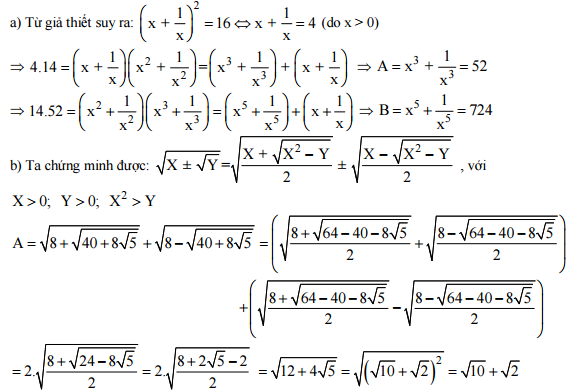
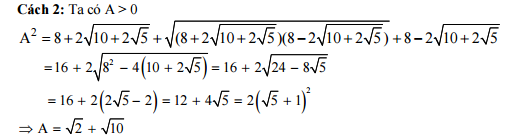
Bài 2:
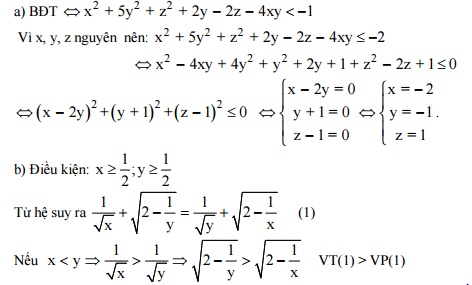

Bài 3:

Bài 4: