Giải Toán 8 trang 92 tập 2 Kết nối tri thức
Giải Toán 8 trang 92 Tập 2
Giải Toán 8 trang 92 Tập 2 Kết nối tri thức hướng dẫn giải chi tiết cho các câu hỏi và bài tập trong SGK Toán 8 Kết nối tri thức tập 2 trang 92.
Bài 9.11 trang 92 Toán 8 tập 2 Kết nối
Cho Δ ABC ∽ Δ DEF. Biết 
\(\widehat{A}=60°, \widehat{E}=80°\) , hãy tính số đo các góc \(\widehat{B} , \ \widehat{C},\ \widehat{D}, \ \widehat{F}\) .
Hướng dẫn giải:
Ta có Δ ABC ∽ Δ DEF nên:
\(\widehat{A}=\widehat{D} =60^{\circ}\)
\(\widehat{B}=\widehat{E} =80^{\circ}\)
\(\widehat{C}=\widehat{F}=180^{\circ} - 60^{\circ} - 80^{\circ} °=40^{\circ}\)
Bài 9.12 trang 92 Toán 8 tập 2 Kết nối
Cho Δ ABC ∽ Δ A'B'C'. Biết AB = 3 cm, A'B' = 6 cm và tam giác ABC có chu vi bằng 10 cm. Hãy tính chu vi tam giác A'B'C'.
Hướng dẫn giải:
Ta có ∆ ABC ∽ ∆ A'B'C' (gt)
⇒ \(\frac{AB}{A'B'}=\frac{BC}{B'C'}=\frac{AC}{A'C'} =\frac{AB+AC+BC}{A'B'+A'C'+B'C'}=\frac{3}{6}\)
Do đó A'B' + A'C' + B'C' = 2(AB + AC + BC) = 2 . 10 = 20 (cm)
Vậy chu vi tam giác A'B'C' là 20 cm.
Bài 9.13 trang 92 Toán 8 tập 2 Kết nối
Cho hình thang ABCD (AB // CD) có \(\widehat{DAB}=\widehat{DBC}\) (H.9.28).
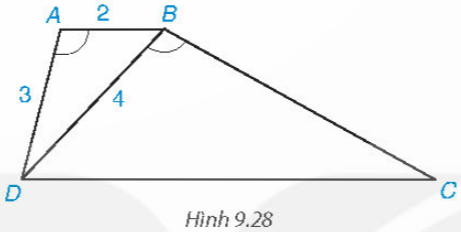
a) Chứng minh rằng ΔABD ∽ ΔBDC
b) Giả sử AB = 2 cm, AD = 3 cm, BD = 4 cm. Tính độ dài các cạnh BC và DC.
Hướng dẫn giải:
a) Ta có AB // CD nên \(\widehat{ABD}=\widehat{BDC}\) (hai góc so le trong)
Xét ΔABD và ΔBDC có:
\(\widehat{ABD}=\widehat{BDC}\) (cmt)
\(\widehat{DAB}=\widehat{DBC}\) (gt)
⇒ Δ ABD ∽ Δ BDC (g . g)
b) Ta có Δ ABD ∽ Δ BDC (cmt)
⇒ \(\frac{AB}{BD}=\frac{AD}{BC}=\frac{BD}{DC}=\frac{2}{4}=\frac{1}{2}\)
Vậy BC = 2AD = 2 . 3 = 6 cm
và DC = 2BD = 2 . 4 = 8 cm.
Bài 9.14 trang 92 Toán 8 tập 2 Kết nối
Cho các điểm A, B, C, D, E, F như Hình 9.29. Biết rằng DE // AB, EF // BC, DE = 4 cm, AB = 6 cm. Chứng minh rằng Δ AEF ∽ Δ ECD và tính tỉ số đồng dạng.
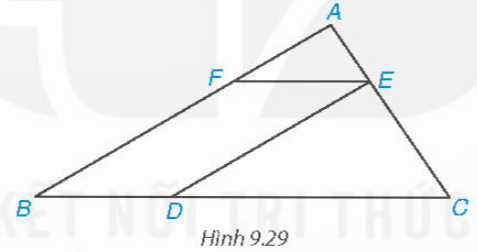
Hướng dẫn giải:
Do BFED là hình bình hành (BF // DE và FE // BD) nên BF = DE = 4 cm
⇒ AF = AB – BF = 6 – 4 = 2 cm
Xét Δ AEF và Δ ECD, có:
\(\widehat{AEF}=\widehat{ECD}\) (hai góc đồng vị)
\(\widehat{EAF}=\widehat{CED}\) (hai góc đồng vị)
⇒ Δ AEF ∽ Δ ECD (g . g)
⇒ \(k=\frac{AE}{EC}=\frac{EF}{CD}=\frac{AF}{ED}=\frac{2}{4}=\frac{1}{2}\).
Bài 9.15 trang 92 Toán 8 tập 2 Kết nối
Cho các điểm A, B, C, D, E như Hình 9.30. Biết rằng \(\widehat{BAC}=\widehat{CDB}\), hãy chứng minh rằng ΔAED ∽ ΔBEC.
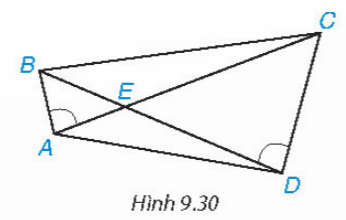
Hướng dẫn giải:
Đang cập nhật...
Bài 9.16 trang 92 Toán 8 tập 2 Kết nối
Cho hình thang ABCD (AB // CD) và các điểm M, N lần lượt trên cạnh AD và BC sao cho 2AM = MD, 2BN = NC. Biết rằng AB = 5 cm, CD = 6 cm, hãy tính độ dài đoạn thẳng MN.
Hướng dẫn giải:
Đang cập nhật...
-----------------------------------------------
Lời giải Toán 8 trang 92 Tập 2 Kết nối tri thức với các câu hỏi nằm trong Giải Toán 8 Kết nối tri thức Luyện tập chung trang 91, được VnDoc biên soạn và đăng tải!
