VnDoc.com

Các bước khảo sát và vẽ đồ thị hàm số bậc 3

Khảo sát và vẽ đồ thị hàm số Toán 12

1 183

CÁC BƯC KHO SÁT Đ TH HÀM S BC 3

A. Lý thuyết

I- SƠ Đ CHUNG KHO SÁT VÀ VẼ Đ TH HÀM S.

1. Tp xác đnh.

2. Sự biến thiên

2.1 Xét chiều biến thiên của hàm số

+ Tính đạo hàm y’

+ Tìm các điểm mà tại đó đạo hàm y’ bằng 0 hoặc không xác định

+ Xét dấu đạo hàm y’ và suy ra chiều biến thiên của hàm số.

2.2 Tìm cực trị

2.3 Tìm các giới hạn tại vô cực ( ), các giới hạn có kết quả là vô cực và tìm

tiệm cận nếu có.

2.4 Lập bảng biến thiên.

Thể hiện đầy đủ và chính xác các giá trị trên bảng biến thiên.

3. Đ th

- Giao của đồ thị với trục Oy: x=0 =>y= ? => (0;?)

- Giao của đồ thị với trục Ox: y = 0 <=> f(x) = 0 <=> x = ? => (?;0 )

- Các điểm CĐ; CT nếu có.

(Chú ý: nếu nghiệm bấm máy tính được thì bấm, nghiệm lẻ giải tay được thì phải giải ra- chẳng

hạn phương trình bậc 2, còn nghiệm lẽ mà không giải được thì ghi ra giấy nháp cho biết giá trị

để khi vẽ cho chính xác- không ghi trong bài- chẳng hạn hàm bậc 3)

- Lấy thêm một số điểm (nếu cần)- (điều này làm sau khi hình dung hình dạng của đồ thị. Thiếu

bên nào học sinh lấy điểm phía bên đó, không lấy tùy tiện mất thời gian.)

- Nhận xét về đặc trưng của đồ thị. Điều này sẽ cụ thể hơn khi đi vẽ từng đồ thị hàm số.

II- SƠ Đ KHO SÁT VÀ VẼ Đ TH HÀM BC BA: y = ax

3

+ bx

2

+ cx + d (a ¹ 0) .

7ҥL  W j L  O L ӉX PL ӇQ SKt  KW W SV    YQGRF  FRP

1. Tp xác đnh. D=R

2. Sự biến thiên

2.1 Xét chiều biến thiên của hàm số

+ Tính đạo hàm:

+ ( Bấm máy tính nếu nghiệm chẵn, giải nếu nghiệm lẻ- không được ghi nghiệm

gần đúng)

+ Xét dấu đạo hàm y’ và suy ra chiều biến thiên của hàm số.

2.2 Tìm cực trị

2.3 Tìm các giới hạn tại vô cực ( )

(Hàm bậc ba và các hàm đa thức không có TCĐ và TCN.)

2.4 Lập bảng biến

Thể hiện đầy đủ và chính xác các giá trị trên bảng biến thiên.

3. Đ th

- Giao của đồ thị với trục Oy: x=0 =>y= d => (0; d)

- Giao của đồ thị với trục Ox: y = 0 <=> ax

3

+ bx

2

+ cx + d = 0 <=> x = ?

- Các điểm CĐ; CT nếu có.

(Chú ý: nếu nghiệm bấm máy tính được 3 nghiệm thì ta bấm máy tính, còn nếu được 1 nghiệm

nguyên thì phải đưa về tích của một hàm bậc nhất và một hàm bậc hai để giải nghiệm. Trường

hợp cả ba nghiệm đều lẻ thì chỉ ghi ra ở giấy nháp để phục vụ cho việc vẽ đồ thị)

- Lấy thêm một số điểm (nếu cần)- (điều này làm sau khi hình dung hình dạng của đồ thị. Thiếu

bên nào học sinh lấy điểm phía bên đó, không lấy tùy tiện mất thời gian.)

- Nhận xét về đặc trưng của đồ thị. Hàm bậc ba nhận điểm làm tâm đối xứng.

+ Trong đó: x

0

là nghiệm của phương trình y’’ = 0 (đạo hàm cấp hai bằng 0)

+ Điểm I được gọi là ‘điểm uốn’ của đồ thị hàm số.

Các dạng đồ thị hàm số bậc 3: y = ax

3

+ bx

2

+ cx + d (a ¹ 0)

7ҥL  W j L  O L ӉX PL ӇQ SKt  KW W SV    YQGRF  FRP

B. Ví dụ minh họa

Ví dụ 1: Khảo sát sự biến thiên và vẽ đồ thị của hàm số : y = x

3

+ 3x

2

– 4

1. Tp xác đnh D = R

2. Sự biến thiên

+)Giới hạn hàm số tại vô cực

7ҥL  W j L  O L ӉX PL ӇQ SKt  KW W SV    YQGRF  FRP

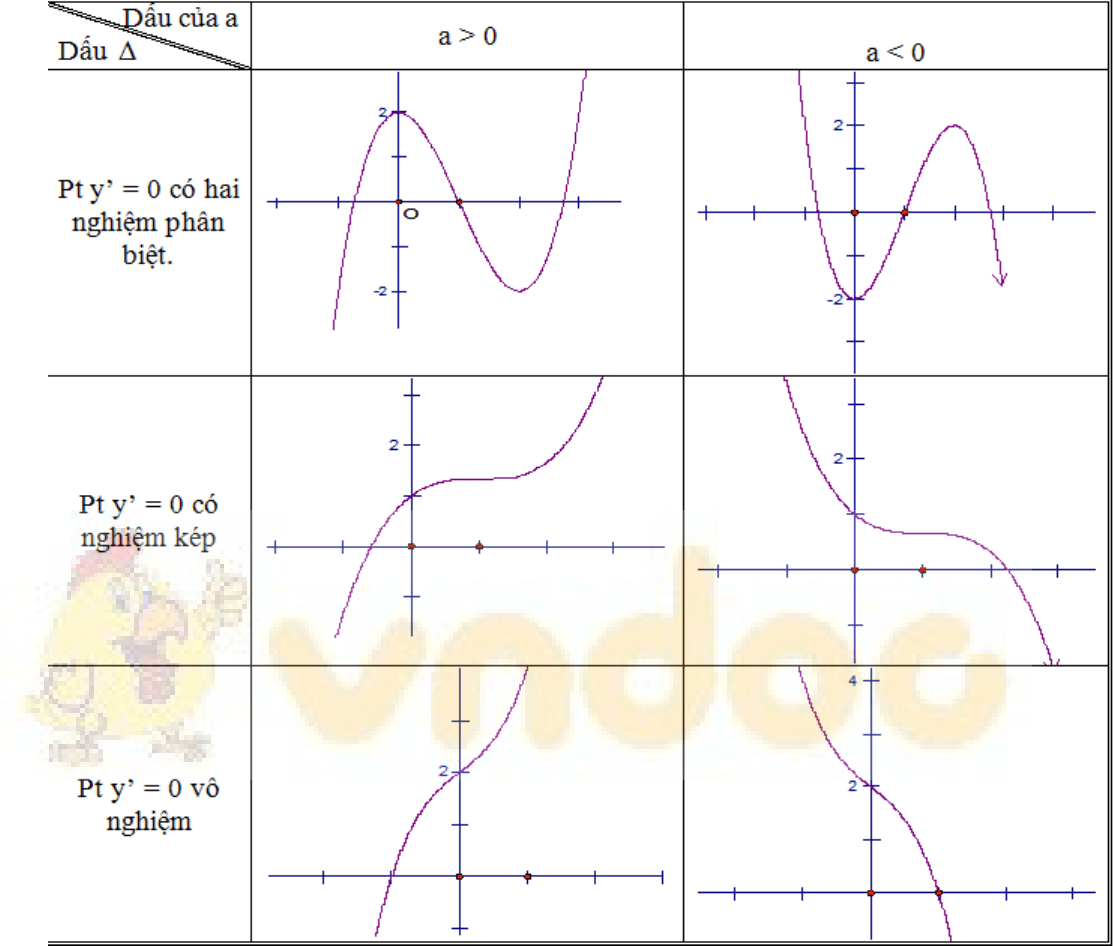
Khảo sát và vẽ đồ thị hàm số bậc 3

Các bước khảo sát và vẽ đồ thị hàm số bậc 3 vừa được VnDoc.com tổng hợp và xin gửi tới bạn đọc cùng tham khảo. Mong rằng qua đây bạn đọc có thêm nhiều tài liệu để học tập nhé. Mời các bạn cùng tham khảo chi tiết và tải về tại đây.

VnDoc.com xin gửi tới bạn đọc bài viết Các bước khảo sát và vẽ đồ thị hàm số bậc 3 để bạn đọc cùng tham khảo. Bài viết được VnDoc.com tổng hợp gồm có lý thuyết khảo sát và vẽ đồ thị hàm số, bài tập vận dụng... Mời các bạn cùng tham khảo chi tiết.

Trên đây VnDoc.com vừa giới thiệu tới các bạn Các bước khảo sát và vẽ đồ thị hàm số bậc 3, mong rằng qua đây các bạn có thêm nhiều tài liệu để học tập môn Toán lớp 12 nhé. Mời các bạn cùng tham khảo thêm các môn Ngữ văn 12, Tiếng Anh 12, đề thi học kì 1 lớp 12, đề thi học kì 2 lớp 12...

Mời bạn đọc cùng tham gia nhóm Tài liệu học tập lớp 12 để có thêm tài liệu học tập nhé