VnDoc.com

Đề thi học kì 1 lớp 10 môn Toán năm 2018 - 2019 trường THPT Chuyên Lê Quý Đôn - Bình Định

Đề kiểm tra học kì 1 môn Toán lớp 10 có đáp án

1 173

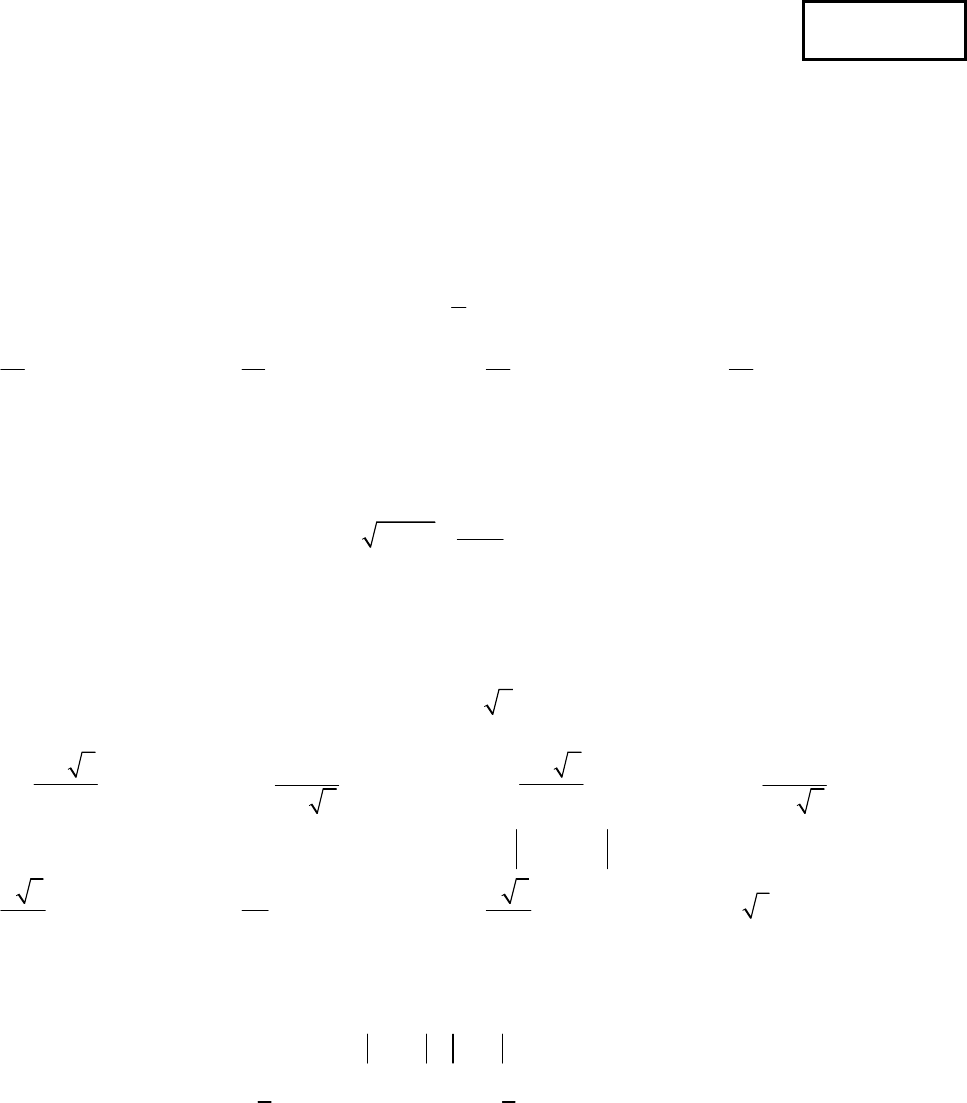
SỞ GIÁO DỤC VÀ ĐÀO TẠO BÌNH ĐỊNH

TRƯỜNG THPT CHUYÊN LÊ QUÝ ĐÔN

Họ tên thí sinh: …..……………………

SBD: ……………… Lớp: ………..

..…

ĐỀ KIỂM TRA HỌC KỲ I , NĂM HỌC 2018-2019

Môn: Toán – Khối: 10

Ngày kiểm tra: 26 /12/2018

Thời gian làm bài: 90 phút

Đề có 3 trang, gồm 34 câu (30 câu TN và 4 câu TL)

Mã đề thi

132

PHẦN I. TRẮC NGHIỆM (6 điểm, 30 câu):

Câu 1: Cho hệ phương trình

3

2 1

mx y

x my m

 





  



với m là tham số. Tìm m để hệ phương trình có nghiệm

duy nhất?

A.

 

1;1;0

 m

B.

m 

C.

 

1;1 .

m  

D.

 

\ 1;1

m

 

.

Câu 2: Cho

0 0

0 180

x 

và thỏa mãn

1

2

sin x cos x

 

. Tính giá trị biểu thức

3 3

S sin x cos x 

A.

11

16

B.

11

13

C.

9

16

D.

13

16

Câu 3: Trong mặt phẳng tọa độ Oxy cho tam giác ABC có trọng tâm G(1; 2). Biết A(2; 2), B(0; - 1), tìm

tọa độ điểm C:

A.

 

5;1

C

B.

 

1;3

C

C.

 

3;2

C

D.

 

1;5

C

Câu 4: Tìm tập xác định D của hàm số

3

2 6

3

  



y x

x

A. D =

 

( 3; ) \ 3

 

B. D =

(3; )

C. D =

 

\ 3

D. D =





3;



Câu 5: Cho hình bình hành

ABCD

có tâm

O

. Chọn hệ thức đúng trong các hệ thức sau:

A.

2 

  

AD AB OC

; B.

2OD OB OA

 

  

; C.

OD OB BD

 

  

; D.

AC BD



 

;

Câu 6: Cho tam giác ABC vuông cân tại B có

2 2

AC

. Tính bán kính đường tròn nội tiếp tam giác

ABC.

A.

2 2

2



r

B.

2

2 2





r C.

2 2

2



r

D.

2

2 2





r

Câu 7: Cho tam giác ABC là tam giác đều cạnh

a

. Khi đó

AC BA



 

bằng:

A.

3

2

a

B.

3

2

a

C.

3

a

D.

3a

Câu 8: Cho phương trình

2

1 0

x x

  

có hai nghiệm

1 2

,x x

. Giá trị

2 2

1 2

x x

bằng:

A.

4

B.

2

C.

3

D.

5

Câu 9: Tổng các nghiệm của phương trình

2x 1 2

x

  

bằng:

A.

4

B.

5

3



C.

8

3



D.

3

Câu 10: Tọa độ giao điểm của parabol (P): y = x

2

– 3x + 2 và đường thẳng y = x – 1 là:

A. (1; 0); (3; 2) B. (0; –1); (–2; –3) C. (–1; 2); (2; 1) D. (2;1); (0; –1).

Câu 11: Trong mặt phẳng tọa độ Oxy cho tam giác ABC có trực tâm H. Tìm tọa độ tâm I của đường tròn

ngoại tiếp tam giác ABC biết A(1;0), H(3;2) và trung điểm BC là M(1; 3).

A. I(1; 3) B. I(3; 1) C. I(2; 0) D. I(0; 2)

Câu 12: Cho hai tập hợp E =

( ;6]

và F =

 

2;7



. Khi đó

E F

là:

A.

E F

=

 

2;6



B.

E F

=

( ;7]

C.

E F

=

 

6;7

D.

E F

=

( ; 2) 

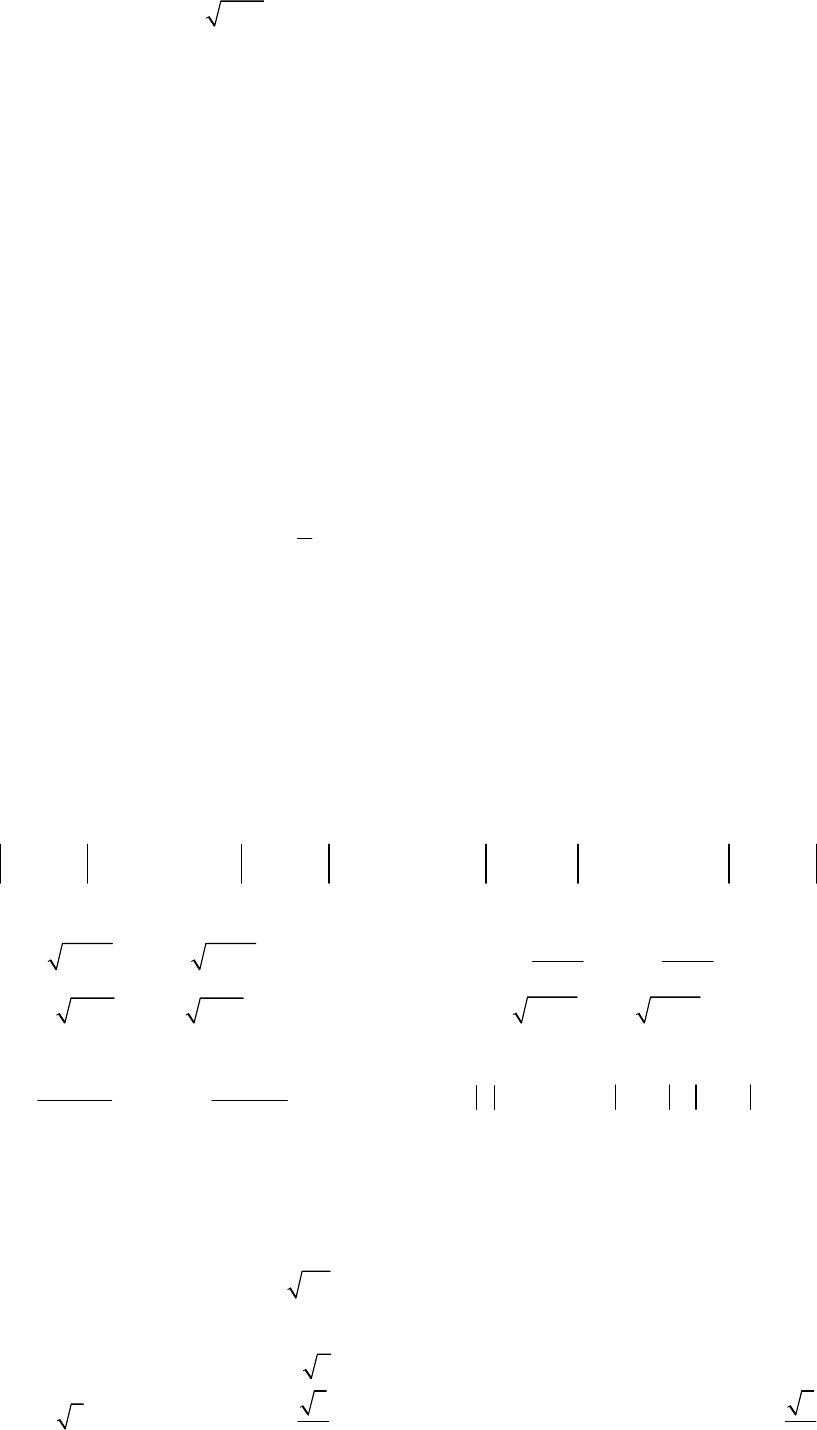
Câu 13: Cho phương trình

1 1x x  

(1). Hãy chọn mệnh đề đúng trong các mệnh đề sau đây:

A. Phương trình (1) có tập xác định là





1;



B. Phương trình (1) tương đương với phương trình

2

1 1x (x )  

C. Tập xác định của phương trình (1) chứa đoạn

 

1 1;



D. Phương trình (1) vô nghiệm.

Câu 14: Cho mệnh đề “

2

, 1 0

x x

   

” . Mệnh đề phủ định của mệnh đề đã cho là :

A. “

2

, 1 0

x x

   

” B. “

2

, 1 0

x x

   

”

C. “

2

, 1 0

x x

   

” D. “

2

, 1 0

x x

   

”

Câu 15: Cho phương trình

2

( 4) 3 1 0

m x m

   

, với m là tham số. Tìm tất cả giá trị m để phương trình

có nghiệm duy nhất.

A.

2m 

B.

 

2; 2

m

 

C.

2

m



 







. D.

2m  

Câu 16: Hai đồ thị hàm số

2

2 3y x x   

và

2

y x m 

(với m là tham số ) có điểm chung khi và chỉ

khi m thỏa mãn :

A.

3

m



B.

7

2

m

 

C.

3

m



D.

0

m



Câu 17: Phương trình

2

( 1) 2 0

x m x m

    

(với m là tham số ) có hai nghiệm trái dấu khi:

A.

0 2m 

. B.

2m 

. C.

2m 

. D.

2m 

.

Câu 18: Cho hàm số

2

– 4 2

y x x

  

. Khẳng định nào sau đây là đúng?

A. Hàm số giảm trên khoảng

 

3;



. B. Hàm số giảm trên khoảng

 

;

 

.

C. Hàm số giảm trên khoảng

 

; 2

D. Hàm số tăng trên khoảng

 

; 6

.

Câu 19: Cho 3 điểm A, B, C thẳng hàng, B nằm giữa A và C sao cho AB = 3a, AC = 4a. Khẳng định nào

sau đây sai:

A.

2AB CB a 

 

B.

4BC BA a 

 

C.

7AB AC a 

 

D.

4BC AB a 

 

Câu 20: Phương trình

2

3x x

tương đương với phương trình nào sau đây:

A.

2

2 3 2

x x x x

    

. B.

2

1 1

3

3 3

x x

  

 

.

C.

2

2 1 6 1x x x x    

D.

2

. 3 3 . 3

x x x x

  

.

Câu 21: Trong các hàm số sau, có bao nhiêu hàm số chẵn?

1)

4

10

x

y

x





; 2)

2

1

;

20





y

x

3)

4

7 2 1;

y x x

   

4)

2 2 .

y x x

   

A. 2. B. 3. C. 1. D. 4.

Câu 22: Cho hình thang vuông ABCD (vuông tại C và D) có CD =

a

. Khi đó tích vô hướng

.

 

AB CD

bằng:

A.

2

a

B.

2

a

C.

0

D.

2

2a

Câu 23: Cho phương trình

 

  

2

4 . 0

x x có tập nghiệm là S. Số phần tử của tập S là:

A. 0. B. 2. C. 3. D. 1.

Câu 24: Cho tam giác ABC có





0 0

2 60 45

AB , B ,C  

. Tính độ dài đoạn AC.

A.

3

AC B.

3

2

AC

C.

3

AC

D.

3

AC

Câu 25: Cho hàm số

2

2 4 1

y x x

  

có đồ thị như hình vẽ bên dưới.

Phương trình

2

2 4 1

x x m  

(với m là tham số) có hai nghiệm khi và chỉ khi m thuộc tập hợp nào

sau đây?

A.

 

3;m

  

. B.

   

3; 0

m   

. C.





0;m

 

D.

 

3;m

 

.

Câu 26: Cho hai vectơ

   

1;0 , 2;0

  

 

x y . Số đo của góc giữa hai vectơ

x



và

y



bằng:

A. 90

0

B. 180

0

C. 45

0

D. 0

0

Câu 27: Đỉnh của parabol

2

2 3y x x   

có tọa độ là:

A.

 

4; 1

B.

 

4;1



C.

 

1;4



D.

 

1;4

Câu 28: Cho tam giác ABC có

3 7 5

AB ,BC ,CA

  

. Gọi

a b c

m ,m ,m

lần lượt là độ dài các đường

trung tuyến đi qua các đỉnh A, B, C của tam giác. Khi đó

2 2 2

a b c

m m m

 

bằng

A.

234

5

B.

125

4

C.

123

5

D.

123

4

Câu 29: Tìm tập nghiệm S của phương trình

3x 1 4 1x x    

.

A. S =

4

3

 

 

 

B. S =

4

1;

3

 

 

 

C. S =



D. S =

 

1

Câu 30: Trong mặt phẳng tọa độ Oxy cho

11 11A( ; ),B( ; )

. Tìm điểm M thuộc trục tung sao cho MA

2

+

MB

2

đạt giá trị bé nhất.

A.

(0;1)

M

B.

(1;0)

M

C.

( 1;0)

M

D.

(0;0)

M

PHẦN II. TỰ LUẬN (4 điểm, 4 câu):

Câu 1. (1 điểm) Khảo sát sự biến thiên và vẽ đồ thị hàm số

2

2 3y x x  

.

Câu 2. (1 điểm) Giải hệ phương trình



  





  





2 2

2 3 4

x x y

y y x

.

Câu 3. (0,5 điểm) Giải phương trình

 

2

8 7 10 6    x x x x

.

Câu 4. (1,5 điểm) Trong mặt phẳng tọa độ Oxy, cho 3 điểm

 

1;2 , ( 2;1), (3;1)

A B C

.

a) Chứng minh rằng A, B, C là 3 đỉnh của một tam giác. Tìm tọa độ điểm D sao cho tứ giác ABCD là hình

bình hành.

b) Tìm tọa độ điểm M để tam giác MAB vuông cân tại M.

----------------------------------------------

----------- HẾT ----------

x

y

1

3

1

O

Đề thi học kì 1 môn Toán lớp 10

VnDoc xin giới thiệu tới bạn đọc Đề thi học kì 1 lớp 10 môn Toán năm 2018 - 2019 trường THPT Chuyên Lê Quý Đôn - Bình Định. Tài liệu gồm 30 câu trắc nghiệm và 4 câu tự luận, thời gian làm bài thi 90 phút. Mời các bạn tham khảo.

-----------------------------

Trên đây VnDoc đã giới thiệu tới các bạn Đề thi học kì 1 lớp 10 môn Toán năm 2018 - 2019 trường THPT Chuyên Lê Quý Đôn - Bình Định. Để có kết quả cao hơn trong học tập, VnDoc xin giới thiệu tới các bạn học sinh tài liệu Giải bài tập Toán 10, Giải bài tập Vật Lí 10, Giải bài tập Sinh học 10, Giải bài tập Hóa học 10, Tài liệu học tập lớp 10 mà VnDoc tổng hợp và đăng tải.