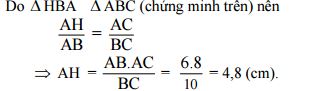Đề thi học kì 2 môn Toán lớp 8 trường PTDTBT THCS Tà Hộc, Mai Sơn năm 2015 - 2016

Đề thi học kì 2 môn Toán lớp 8

Đề thi học kì 2 môn Toán lớp 8 trường PTDTBT THCS Tà Hộc, Mai Sơn năm 2015 - 2016 là đề kiểm tra cuối học kì II lớp 8 môn Toán có đáp án. VnDoc xin giới thiệu tới các bạn tài liệu này giúp các bạn ôn thi học kì 2 môn Toán lớp 8 tốt hơn, đạt điểm cao trong bài thi của mình. Mời các bạn tham khảo.

Đề thi học kì 2 môn Công nghệ lớp 8 trường PTDTNT THCS Huyện Duyên Hải năm 2015 - 2016

Đề thi học kì 2 môn Địa lý lớp 8 trường THCS Hồng Dương, Hà Nội năm 2015 - 2016

PHÒNG GD&ĐT MAI SƠN
TRƯỜNG PTDTBT THCS TÀ HỘC

ĐỀ KIỂM TRA HỌC KỲ II
Năm học: 2015 – 2016
Môn: Toán - Lớp: 8
Thời gian: 90 phút (không kể thời gian chép đề)
(Đề gồm 01 trang)

Đề số: 01

Câu 1: (1 điểm)

a) Phát biểu định lí về tính chất của đường phân giác trong tam giác?

b) Viết công thức tính diện tích xung quanh của hình lăng trụ đứng.

Câu 2: (1,5 điểm)

a) Nêu định nghĩa phương trình bậc nhất một ẩn. Lấy ví dụ minh họa.

b) Thế nào là hai bất phương trình tương đương?

Câu 3: (2 điểm) Giải các bất phương trình sau:

a) 5(x + 1) < 3x + 13; b) x² + 3x – 10 < (x + 2)(x – 2)

Câu 4: (2 điểm) Một người đi xe đạp từ A đến B với vận tốc 15 km/h. Lúc về người đó đi với vận tốc 12 km/h, nên thời gian đi ít hơn thời gian về là 30 phút. Tính độ dài đoạn đường AB.

Câu 5: (1 điểm) Cho hình lăng trụ đứng ABCD.A'B'C'D'có đáy là hình chữ nhật. Biết AB = 3cm, BC = 4 cm, AA' = 5cm. Tính diện tích xung quanh và thể tích của hình lăng trụ.

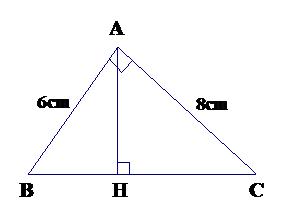
Câu 6: (2,5 điểm) Cho ΔABC vuông tại A, có AB = 6 cm; AC = 8 cm. Kẻ đường cao AH (H ∈ BC).

a) Chứng minh: ΔHBA ~ ΔABC

b) Tính độ dài các đoạn thẳng BC, AH.

Đáp án đề thi học kì 2 môn Toán lớp 8

Đề thi học kì 2 môn Toán lớp 8 phòng GD&ĐT Tam Đảo, Vĩnh Phúc năm 2015 - 2016

Đề thi học kì 2 môn Ngữ văn lớp 8 phòng GD&ĐT Cam Lộ, Quảng Trị năm 2015 - 2016

Câu 1:

a) Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề hai đoạn ấy. (0,5đ)

b) Công thức tính diện tích xung quanh của hình lăng trụ đứng: (0,5đ)

S_xq = 2p.h

(p là nửa chu vi đáy, h là chiều cao)

Câu 2:

a) Phương trình dạng ax + b = 0, với a, b là hai số đã cho và a ≠ 0, được gọi là phương trình bậc nhất một ẩn. (0,5đ)

Ví dụ: Phương trình 2x + 3 = 0 là phương trình bậc nhất một ẩn. (0,5đ)

b) Hai bất phương trình tương đương là hai bất phương trình có cùng tập nghiệm. (0,5đ)

Câu 3:

a) 5(x + 1) < 3x + 13 ↔ 5x + 5 < 3x + 13 (0,25đ)

↔ 5x – 3 x < 13 – 5 (0,25đ)

↔ 2x < 8 x < 4 (0,25đ)

Vậy nghiệm của bất phương trình đã cho là x < 4. (0,25đ)

b) x² + 3x – 10 < (x + 2)(x – 2) ↔ x² + 3x – 10 < x² – 4 (0,25đ)

↔ x² – x² + 3x < 10 – 4 (0,25đ)

↔ 3x < 6 x < 2. (0,25đ)

Vậy nghiệm của bất phương trình đã cho là x < 2. (0,25đ)

Câu 4:

Gọi x (km) là độ dài đoạn đường AB, x > 0. (0,25đ)

Thời gian đi từ A đến B là x/15 giờ. (0,25đ)

Thời gian về từ B đến A là x/12 giờ. (0,25đ)

Vì thời gian đi ít hơn thời gian về là 30 phút = 1/2 h nên ta có phương trình: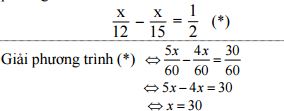
(1,0đ)

ta được x = 30 (thỏa mãn điều kiện của ẩn).

Vậy độ dài đoạn đường AB là 30 km. (0,25đ)

Câu 5:

Diện tích xung quanh của hình lăng trụ đứng là:

S_xq = 2p.h = 2.(AB + BC).AA' = 2.(3 + 4).5 = 70 (cm²). (0,5đ)

Thể tích của hình lăng trụ đứng là:

V = S.h = AB.AC.AA' = 3.4.5 = 60 (cm³) (0,5đ)

Câu 6:

GT: ΔABC, ∠A= 90^o
AB = 6 cm, AC = 8 cm
AH ⊥ BC (H ∈ BC)

KL:
a) ΔHBA ~ΔABC
b) Tính BC, AH.

Chứng minh:

a) Xét ΔHBA và ΔABC có:

∠BAC = ∠BHA= 90^o (gt) (0,25đ)

∠B: góc chung (0,25đ)

=> ΔHBA ~ΔABC (trường hợp đồng dạng thứ 3) (0,25đ)

b) Trong ΔABC, ∠A= 90^o ta có:

BC² = AB² + AC² (định lí Py-ta-go) (0,25đ)

BC² = 62 + 82 = 36 + 64 = 100 (0,25đ)

BC = √100 = 10 (cm) (0,25đ)