Đề thi học sinh giỏi lớp 10 THPT Chuyên tỉnh Vĩnh Phúc năm 2012 môn Toán - Có đáp án

Vndoc.com xin giới thiệu đến các bạn lớp 9, chuẩn bị thi lên lớp 10: Đề thi học sinh giỏi lớp 10 THPT Chuyên tỉnh Vĩnh Phúc năm 2012 môn Toán - Có đáp án.

Đề thi học sinh giỏi lớp 10 môn Toán:

Câu 1 (3,0 điểm)

1. Giải hệ phương trình: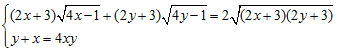

2. Tìm tất cả hàm số f: ¡ → ¡ thoả mãn: f(x + y) = f(x) + y với mọi x, y thuộc ¡ và

Câu 2 (2,0 điểm)

Tìm tất cả các số nguyên tố p, q sao cho (7^p - 4^p)(7^q - 4^q) chia hết cho pq.

Câu 3 (2,0 điểm).

Cho tứ giác ABCD ngoại tiếp được một đường tròn. Một đường thẳng Δ đi qua A cắt đoạn thẳng BC, tia đối của tia CD tương ứng tại E, F (E, F không trùng với B, C). Gọi I₁, I₂ và I₃ lần lượt là tâm đường tròn nội tiếp của các tam giác ABE, ECF và FAD. Tiếp tuyến của đường tròn song song với CD (gần CD hơn) cắt Δ tại H. Chứng minh rằng H là trực tâm của tam giác I₁I₂I₃

Câu 4 (2,0 điểm).

Xét các số thực dương a, b, c thỏa mãn a + 2b + 3c ≥ 20. Tìm giá trị nhỏ nhất của biểu thức:

Câu 5 (1,0 điểm).

Tìm tất cả các tập hợp X là tập con của tập số nguyên dương thoả mãn các tính chất: X chứa ít nhất hai phần tử và với mọi m, n thuộc X, m < n thì tồn tại k thuộc X sao cho n = mk².