VnDoc.com

Đề thi khảo sát chất lượng lớp 9 môn Toán Phòng GD&ĐT Hưng Nguyên năm học 2019 - 2020

Đề thi khảo sát lớp 9 môn Toán có đáp án

Bài trước

Bài sau

Đề khảo sát chất lượng lớp 9 môn Toán Phòng GD&ĐT Hưng Nguyên năm 2020

Thư viện đề thi VnDoc xin giới thiệu Đề thi khảo sát chất lượng lớp 9 môn Toán Phòng GD&ĐT Hưng Nguyên, Nghệ An năm học 2019 - 2020. Đây là đề kiểm tra KSCL môn Toán lớp 9 dành cho các bạn học sinh ôn tập, củng cố kiến thức, rèn luyện kĩ năng làm bài Toán. Mời các bạn cùng tham khảo

Đề thi khảo sát chất lượng lớp 9 môn Văn Phòng GD&ĐT Hưng Nguyên năm học 2019 - 2020

Để tiện trao đổi, chia sẻ kinh nghiệm về giảng dạy và học tập các môn học lớp 9, VnDoc mời các thầy cô giáo, các bậc phụ huynh và các bạn học sinh truy cập nhóm riêng dành cho lớp 9 sau: Nhóm Tài liệu học tập lớp 9. Rất mong nhận được sự ủng hộ của các thầy cô và các bạn.

PHÒNG GIÁO DỤC VÀ ĐÀO TẠO

HƯNG NGUYÊN

ĐỀ KHẢO SÁT CHẤT LƯỢNG HỌC SINH LỚP 9

NĂM HỌC 2020 - 2021

Câu 1 (2,5 điểm)

1) Rút gọn các biểu thức sau

$a)\ A = 3\sqrt 8 - \sqrt {50} - \sqrt{(\sqrt 2 - 1)^2}$ $a)\ A = 3\sqrt 8 - \sqrt {50} - \sqrt{(\sqrt 2 - 1)^2}$

$b)\ P = \dfrac{x}{\sqrt x -1} - \dfrac{2x-\sqrt x}{x-\sqrt x} với x >0 ; \space x ≠ 1$ $b)\ P = \dfrac{x}{\sqrt x -1} - \dfrac{2x-\sqrt x}{x-\sqrt x} với x >0 ; \space x ≠ 1$

2) Tìm toạ độ giao điểm của đường thẳng $(d): y = 3x + 2$ và đường thẳng $(d'): y = 2x - 7$.

Câu 2 (2,0 điểm) Cho phương trình $x^2 - 5mx - 4m = 0 (1)$

a) Giải phương trình khi m = -1.

b) với $x_1; x_2$ là hai nghiệm phân biệt của phương trình (1). Chứng minh rằng:

$x_1^2 + 5mx_2 - 4m > 0$

Câu 3 (1,5 điểm)

Hưởng ứng lời kêu gọi của Uỷ ban Mặt trận Tổ quốc Việt Nam về ủng hộ phòng chống dịch Covid-19. Học sinh trường THCS Nguyễn Du đã quyên góp được 120 hộp khẩu trang y tế và 120 hộp khẩu trang vải sát khuẩn trong thời gian 7 ngày. Biết rằng, mỗi ngày quyên góp được số hộp khẩu trang y tế ít hơn số hộp khẩu trang vải sát khuẩn là 10 hộp. Hỏi mỗi ngày học sinh trường THCS Nguyễn Du đã quyên góp được bao nhiêu hộp khẩu trang y tế và bao nhiêu hộp khẩu trang vải sát khuẩn.

Câu 4 (3,0 điểm)

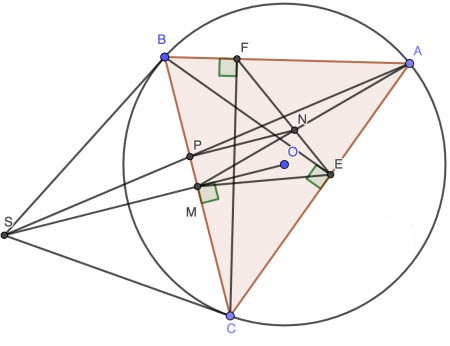
Cho tam giác ABC có ba góc nhọn nội tiếp đường tròn (O), BE và CF là các đường cao. Các tiếp tuyến tại B và tại C của đường tròn (O) cắt nhau tại S. Các đường thẳng BC và OS cắt nhau tại M.

a) Chứng minh rằng tứ giác BCEF nội tiếp.

b) Chứng minh rằng $\dfrac{AS}{AM} = \dfrac{BS}{BM} .$ $\dfrac{AS}{AM} = \dfrac{BS}{BM} .$

c) Gọi N là giao điểm của AM và EF, P là giao điểm của AS và BC. Chứng minh rằng NP ⊥ BC.

Câu 5 (1,0 điểm)

Cho hai số thực dương x và y thoả mãn x + y = 1.

Tìm giá trị nhỏ nhất của biểu thức:

$A = \dfrac{1}{x^2+y^2} + \dfrac{1}{xy}$ $A = \dfrac{1}{x^2+y^2} + \dfrac{1}{xy}$

Hết

Đáp án đề thi thử vào lớp 10 môn Toán 2020 huyện Hưng Nguyên

Câu 1:

1)

$a)\ A = 3\sqrt 8 - \sqrt {50} - \sqrt{(\sqrt 2 - 1)^2}$ $a)\ A = 3\sqrt 8 - \sqrt {50} - \sqrt{(\sqrt 2 - 1)^2}$

$= 6\sqrt 2 - 5\sqrt {2} - {(\sqrt 2 - 1)} =1$ $= 6\sqrt 2 - 5\sqrt {2} - {(\sqrt 2 - 1)} =1$

b) Với $x >0 ; \space x ≠ 1$ $x >0 ; \space x ≠ 1$, ta có:

$P = \dfrac{x}{\sqrt x -1} - \dfrac{2x-\sqrt x}{x-\sqrt x}$ $P = \dfrac{x}{\sqrt x -1} - \dfrac{2x-\sqrt x}{x-\sqrt x}$

$= \dfrac{x}{\sqrt x -1} - \dfrac{2\sqrt x-1}{\sqrt x-1}$ $= \dfrac{x}{\sqrt x -1} - \dfrac{2\sqrt x-1}{\sqrt x-1}$

$= \dfrac{x - 2\sqrt x+1}{\sqrt x-1}$ $= \dfrac{x - 2\sqrt x+1}{\sqrt x-1}$

$= \dfrac{(\sqrt x-1)^2}{\sqrt x-1} = \sqrt x-1$ $= \dfrac{(\sqrt x-1)^2}{\sqrt x-1} = \sqrt x-1$

2)

Toạ độ giao điểm của (d) và (d') là nghiệm của hệ:

$\left\{ \matrix{ y = 3x+2 \hfill \cr y = 2x - 7 \hfill \cr} \right.$ $\left\{ \matrix{ y = 3x+2 \hfill \cr y = 2x - 7 \hfill \cr} \right.$

$\Leftrightarrow \left\{ \matrix{ x = -9 \hfill \cr y = -25 \hfill \cr} \right.$ $\Leftrightarrow \left\{ \matrix{ x = -9 \hfill \cr y = -25 \hfill \cr} \right.$

KL......

Câu 2:

a)

Với m = -1, thay vào (1) ta có:

$x^2 + 5x + 4 = 0$

$\Leftrightarrow \left[ \matrix{ x = -1 \hfill \cr x = -4 \hfill \cr} \right.$ $\Leftrightarrow \left[ \matrix{ x = -1 \hfill \cr x = -4 \hfill \cr} \right.$

KL.......

b)

Để phương trình (1) có hai nghiệm phân biệt khi và chỉ khi:

$\Delta = (5m)^2 + 4.4m = m(25m + 16) > 0$ $\Delta = (5m)^2 + 4.4m = m(25m + 16) > 0$

$\Leftrightarrow \left[ \matrix{ m>0 \hfill \cr m < \dfrac{-16}{25} \hfill \cr} \right.$ $\Leftrightarrow \left[ \matrix{ m>0 \hfill \cr m < \dfrac{-16}{25} \hfill \cr} \right.$

Áp dụng hệ thức Vi-ét cho (1), ta có:

$\left\{ \matrix{ x_1+x_2 = 5m \hfill \cr x_1x_2 = -4m \hfill \cr} \right.$ $\left\{ \matrix{ x_1+x_2 = 5m \hfill \cr x_1x_2 = -4m \hfill \cr} \right.$

Thay vào ta có:

$x_1^2 + 5mx_2 - 4m = x_1^2 + (x_1+x_2) x_2 + x_1x_2$

$= x_1^2 + x_2^2 + 2x_1x_2 = (x1+x2)^2 = 25m^2$

Dễ thấy với $m>0 ∨ m < \dfrac{-16}{25}$ $m>0 ∨ m < \dfrac{-16}{25}$ thì

$25m^2 > 0 \Leftrightarrow x_1^2 + 5mx_2 - 4m > 0 (đpcm)$ $25m^2 > 0 \Leftrightarrow x_1^2 + 5mx_2 - 4m > 0 (đpcm)$

Câu 3:

Gọi số hộp khẩu trang y tế và hộp khẩu trang vải sát khuẩn mỗi ngày học sinh trường THCS Nguyễn Du quyên góp được lần lượt là A và B (hộp; A,B > 0)

Số ngày quyên góp khẩu trang y tế là $\dfrac{120}A$ $\dfrac{120}A$ (ngày)

Số ngày quyên góp khẩu trang vải sát khuẩn là $\dfrac{120}B$ $\dfrac{120}B$ (ngày)

Theo bài ra ta có:

$\left\{ \matrix{ B-A = 10 \hfill \cr \dfrac{120}A + \dfrac{120}B = 7 \hfill \cr} \right.$ $\left\{ \matrix{ B-A = 10 \hfill \cr \dfrac{120}A + \dfrac{120}B = 7 \hfill \cr} \right.$

$\Leftrightarrow \left\{ \matrix{ B = 10 + A \hfill \cr \dfrac{120}A + \dfrac{120}{10+A} = 7 \hfill \cr} \right.$ $\Leftrightarrow \left\{ \matrix{ B = 10 + A \hfill \cr \dfrac{120}A + \dfrac{120}{10+A} = 7 \hfill \cr} \right.$

$\Leftrightarrow \left\{ \matrix{ B = 10 + A \hfill \cr 7A^2 -170A - 1200 = 0 \hfill \cr} \right.$ $\Leftrightarrow \left\{ \matrix{ B = 10 + A \hfill \cr 7A^2 -170A - 1200 = 0 \hfill \cr} \right.$

$\Leftrightarrow \left\{ \matrix{ B = 10 + A \hfill \cr \left[ \matrix{ A = 30 \space (tm) \hfill \cr A =\dfrac{-40}7 \space (loại) \hfill \cr} \right. \hfill \cr} \right.$ $\Leftrightarrow \left\{ \matrix{ B = 10 + A \hfill \cr \left[ \matrix{ A = 30 \space (tm) \hfill \cr A =\dfrac{-40}7 \space (loại) \hfill \cr} \right. \hfill \cr} \right.$

$\Leftrightarrow \left\{ \matrix{ B = 40 \hfill \cr A= 30 \hfill \cr} \right.$ $\Leftrightarrow \left\{ \matrix{ B = 40 \hfill \cr A= 30 \hfill \cr} \right.$

KL......

Câu 4:

Đề thi khảo sát chất lượng lớp 9 môn Toán Phòng GD&ĐT Hưng Nguyên năm học 2019 - 2020

a)

Vì BE và CF là đường cao của $△ABC ⇒ ∠BEC = ∠BFC = 90° ⇒ E$, F cùng thuộc đường tròn đường kính BC, hay tứ giác BCEF nội tiếp (đpcm).

b)

Theo tính chất tiếp tuyến, ta có OS ⊥ BC tại M, đồng thời M là trung điểm BC.

Xét △BEC vuông tại E, ta có BM = ME = MC và ∠MEC = ∠BCE.

Xét △BAE và △SCM, có:

$∠BEA = ∠SMC = 90°$

∠BAE = ∠BCS (góc tạo bởi tiếp tuyến và dây cung)

Suy ra $△BAE ∽ △SCM ⇒ \dfrac{BA}{AE} = \dfrac{SC}{CM} = \dfrac{SB}{EM} ⇒ \dfrac{BA}{BS} = \dfrac{AE}{EM}$ $△BAE ∽ △SCM ⇒ \dfrac{BA}{AE} = \dfrac{SC}{CM} = \dfrac{SB}{EM} ⇒ \dfrac{BA}{BS} = \dfrac{AE}{EM}$

Theo tính chất góc tạo bởi tiếp tuyến và dây cung cùng chắn cung BC, ta có ∠BAC = ∠CBS

Ta có: $∠AEM = 180° - ∠MEC = 180° - ∠BCE = ∠ABC + ∠BAC = ∠ABC + ∠CBS = ∠ABS.$

Xét △BAS và △EAM, có:

$∠AEM = ∠ABS (cmt)$

$\dfrac{BA}{BS} = \dfrac{AE}{EM} (cmt)$ $\dfrac{BA}{BS} = \dfrac{AE}{EM} (cmt)$

Suy ra $△BAS ∽ △EAM ⇒ \dfrac{AS}{AM} = \dfrac{BS}{EM} = \dfrac{BS}{BM} (đpcm).$ $△BAS ∽ △EAM ⇒ \dfrac{AS}{AM} = \dfrac{BS}{EM} = \dfrac{BS}{BM} (đpcm).$

c)

Vì $△BAS ∽ △EAM ⇒ ∠MAE = ∠SAB$ hay $∠NAE = ∠PAB$

Vì tứ giác BCEF nội tiếp (cm pa) $⇒ ∠FBC = 180° - ∠FEC = ∠FEA$ hay $∠ABP = ∠AEN.$

Vì $△BAS ∽ △EAM (cmt) ⇒ \dfrac{AB}{AE} = \dfrac{AS}{AM} .$ $△BAS ∽ △EAM (cmt) ⇒ \dfrac{AB}{AE} = \dfrac{AS}{AM} .$

Xét △BAP và △EAN có:

∠NAE = ∠PAB

∠ABP = ∠AEN

Suy ra $△BAP ∽ △EAN ⇒ \dfrac{AP}{AN} = \dfrac{AB}{AE} = \dfrac{AS}{AM} ⇒ NP // SM$ $△BAP ∽ △EAN ⇒ \dfrac{AP}{AN} = \dfrac{AB}{AE} = \dfrac{AS}{AM} ⇒ NP // SM$, mà $SM ⊥ BC ⇒ NP ⊥ BC (đpcm).$

Câu 5:

Áp dụng BĐT AM-GM ta có:

$xy \leq \left(\dfrac{x+y}2 \right)^2 = \dfrac{1}4$ $xy \leq \left(\dfrac{x+y}2 \right)^2 = \dfrac{1}4$

Ta lại có

$x^2 + y^2 > 0 \Leftrightarrow (x+y)^2 - 2xy = 1-2xy >0$ $x^2 + y^2 > 0 \Leftrightarrow (x+y)^2 - 2xy = 1-2xy >0$

Ta có:

$A = \dfrac{1}{x^2+y^2} + \dfrac{1}{xy}$ $A = \dfrac{1}{x^2+y^2} + \dfrac{1}{xy}$

$= \dfrac{1}{(x+y)^2 - 2xy} + \dfrac{1}{xy} = \dfrac{1}{1 - 2xy} + \dfrac{1}{xy} = \dfrac{1-xy}{(1 - 2xy)xy}$ $= \dfrac{1}{(x+y)^2 - 2xy} + \dfrac{1}{xy} = \dfrac{1}{1 - 2xy} + \dfrac{1}{xy} = \dfrac{1-xy}{(1 - 2xy)xy}$

Ta đi chứng minh $A \geq 6$ $A \geq 6$

$\Leftrightarrow \dfrac{1-xy}{(1 - 2xy)xy} \geq 6$ $\Leftrightarrow \dfrac{1-xy}{(1 - 2xy)xy} \geq 6$

$\Leftrightarrow {1-xy} \geq 6{(1 - 2xy)xy}$ $\Leftrightarrow {1-xy} \geq 6{(1 - 2xy)xy}$

$\Leftrightarrow 12(xy)^2 - 7xy + 1 \geq 0$ $\Leftrightarrow 12(xy)^2 - 7xy + 1 \geq 0$

$\Leftrightarrow (4xy-1)(3xy-1) \geq 0 (1)$ $\Leftrightarrow (4xy-1)(3xy-1) \geq 0 (1)$

Với $xy \leq \dfrac{1}4 ⇒ (1)$ $xy \leq \dfrac{1}4 ⇒ (1)$ luôn đúng. Mà các phép biến đổi là tương đương, tức là:

$A \geq 6 (đpcm).$ $A \geq 6 (đpcm).$

Vậy ${min}_A = 6 \Leftrightarrow x = y = \dfrac{1}2.$ ${min}_A = 6 \Leftrightarrow x = y = \dfrac{1}2.$

Đề thi khảo sát chất lượng lớp 9 môn Toán Phòng GD&ĐT Hưng Nguyên, Nghệ An năm học 2019 - 2020. Đề thi gồm 5 câu hỏi tự luận với 120 phút làm bài kèm theo đáp án được VnDoc chia sẻ giúp các bạn học sinh ôn tập, biết cách phân bổ thời gian làm bài. Mời các bạn cùng tham khảo

.......................................................................

Ngoài Đề thi khảo sát chất lượng lớp 9 môn Toán Phòng GD&ĐT Hưng Nguyên, Nghệ An năm học 2019 - 2020. Mời các bạn học sinh còn có thể tham khảo các đề thi học học kì 1 lớp 9, đề thi học học kì 2 lớp 9 các môn Toán, Văn, Anh, Hóa, Lý, Địa, Sinh mà chúng tôi đã sưu tầm và chọn lọc. Với đề thi học kì 1, 2 lớp 9 này giúp các bạn rèn luyện thêm kỹ năng giải đề và làm bài tốt hơn. Chúc các bạn ôn thi tốt