Đề thi học kì 2 lớp 9 môn Toán Sở GD&ĐT Bến Tre năm học 2019 - 2020

Đề thi học kì 2 lớp 9 môn Toán Sở GD&ĐT Bến Tre năm học 2019 - 2020 được VnDoc sưu tầm và đăng tải xin gửi tới bạn đọc cùng tham khảo. Nội dung đề thi gồm có 5 câu hỏi tự luận, với thời gian làm bài thi là 90 phút. Tài liệu có đáp án kèm theo, sẽ giúp ích cho các bạn học sinh ôn tập thử sức với các đề thi khác nhau, so sánh đối chiếu với kết quả bài làm của mình. Sau đây là nội dung đề thi mời các bạn tham khảo chi tiết bài viết dưới đây nhé.

• Đề thi học kì 2 lớp 9 môn Toán Sở GD&ĐT Bến Tre năm học 2021-2022
• Đề thi học kì 2 lớp 9 môn Văn Sở GD&ĐT Bến Tre năm học 2019 - 2020

Đề thi học kì 2 lớp 9 môn Toán Sở GD&ĐT Bến Tre năm 2020

SỞ GIÁO DỤC VÀ ĐÀO TẠO BẾN TRE

ĐỀ KIỂM TRA HỌC KỲ II NĂM HỌC 2019 - 2020 MÔN: TOÁN LỚP 9 Thời gian làm bài: 90 phút (không kể thời gian giao đề)

Câu 1 (1,5 điểm)

Trong Hình 1, hãy nhận xét một vài đặc điểm của đồ thị hàm số \(y = f(x) = \dfrac{1}{3}x^2\) bằng cách trả lời các câu hỏi sau:

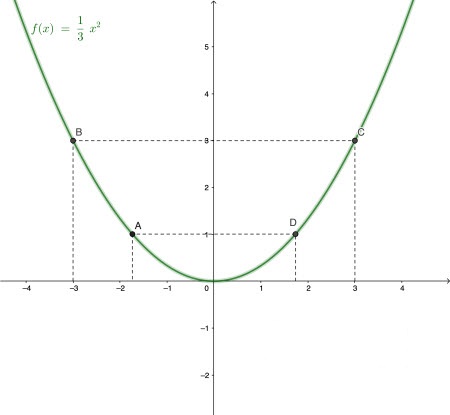
a) Đồ thị nằm phía trên hay phía dưới trục hoành?

b) Tính \(f(3)\)

c) Điểm nào là điểm thấp nhất của đồ thị?

Câu 2 (3,0 điểm)

a) Giải phương trình \(3x^2 + 5x - 9 = 0\)

b) Gọi \(x1,x2\) là hai nghiệm của phương trình \(x^2 - 4x - 2 = 0\). Không giải phương trình hãy tính:

\(\dfrac{2020}{x_1}+\dfrac{2020}{x_2}\)

c) Giải hệ phương trình \(\left\{ \matrix{ 3x + 2y = 23 \hfill \cr x - 2y = 6 \hfill \cr} \right.\)

Câu 3 (2,5 điểm)

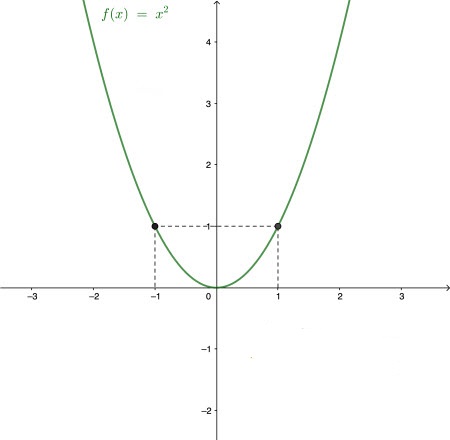
Cho parabol \((P): y=x^2\) và đường thẳng \((d): y = -x + 7\)

a) Vẽ P

b) Điểm A (4;16) có thuộc (P), (d) hay không?

Câu 4 (0,5 điểm)

Trên đường tròn (O;R) lấy các điểm A, B, C sao cho \(∠AOB = 90°, ∠BAC = 30°\). Tính số đo góc CBO.

Câu 5 (2,5 điểm)

Cho đường tròn (O; R) đường kính AB, lấy điểm M thuộc (O) sao cho \(∠MAB = 30⁰\). Gọi C là điểm đối xứng với điểm O qua điểm B. Qua điểm C, vẽ đường thẳng vuông góc với AB cắt đường thẳng AM tại D.

a) Chứng minh tứ giác BCDM nội tiếp trong đường tròn tâm I. Xác định vị trí điểm I .

b) Chứng minh: \(AD.AM = 6R²\)

c) Tính số đo của góc \(ADC\).

Hết

Đáp án đề khảo sát học sinh lớp 9 môn Toán 2020 tỉnh Bến Tre

Câu 1:

a) Đồ thị nằm phía trên trục hoành.

b) \(f(3) = 3\).

c) \(O(0;0)\) là điểm thấp nhất của đồ thị.

Câu 2:

a) \(3x^2 + 5x - 9 = 0\)

\(\Leftrightarrow \left[ \matrix{ {x} = \dfrac{-5+\sqrt{133}}6\hfill \cr {x} = \dfrac{-5-\sqrt{133}}6 \hfill \cr} \right.\)

b)

Ta có \(\Delta' = 2^2 + 2 = 8 >0 ⇒\) phương trình đã cho luôn có hai nghiệm phân biệt.

Áp dụng hệ thức Vi-ét, ta có:

\(\left\{ \matrix{ x_1+ x_2 = 4 \hfill \cr x_1 x_2 = -2 \hfill \cr} \right.\)

Ta có:

\(\dfrac{2020}{x_1}+\dfrac{2020}{x_2} = \dfrac{2020(x_1+x_2)}{x_1x_2} = \dfrac{2020.4}{-2}=-4040\)

\(c) \left\{ \matrix{ 3x + 2y = 23 \hfill \cr x - 2y = 6 \hfill \cr} \right.\)

\(\Leftrightarrow \left\{ \matrix{ x= \dfrac{29}4 \hfill \cr y= \dfrac{5}8 \hfill \cr} \right.\)

Câu 3:

a) Vẽ P

b)

Ta có \(\left\{ \matrix{ x_A = 4 \hfill \cr y_A = 16 \hfill \cr} \right.\)

Ta thấy \(y_A = x_A^2 ⇒\) điểm A thuộc (P).

và \(y_A ≠ -x_A + 7 ⇒\) điểm A không thuộc (d).

Câu 4:

(Các em có thể vẽ hình:

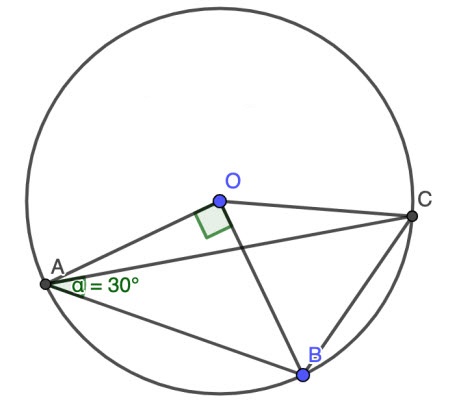
Ta có:

\(∠CBO = \dfrac{180°- ∠BOC}2 = 90° - ∠BAC = 60°\)

Câu 5:

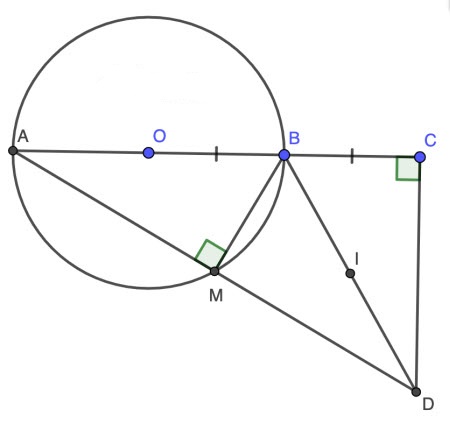
a)

Vì AB là đường kính của (O) nên \(∠AMB = 90°\)

Theo giả thiết có BC ⊥ CD hay \(∠BCD = 90°\)

Ta có \(∠BCD = ∠BMD = 90° ⇒ M, C\) cùng thuộc đường tròn đường kính BD, hay tứ giác BCDM nội tiếp (đpcm).

Lấy I là trung điểm BD, dễ thấy I chính là tâm đường tròn ngoại tiếp tứ giác BCDM.

b)

Vì C và O đối xứng với nhau qua \(B ⇒ CB = BC = OA.\)

Xét △AMB và △ACD, có:

Góc MAB chung

\(∠ACD = ∠AMB (= 90°)\)

Suy ra

\(△AMB ∽ △ACD ⇒ \dfrac{AM}{AB} =\dfrac{AC}{AD} ⇒ AD.AM = AB.AC = 2R.3R = 6R² (đpcm).\)

c)

Xét △ADC vuông tại C, ta có:

\(∠ADC = 90° - ∠DAC = 90° - 30° = 60°\)

...........................

Trên đây VnDoc.com vừa gửi tới bạn đọc bài viết Đề thi học kì 2 lớp 9 môn Toán Sở GD&ĐT Bến Tre năm học 2019 - 2020. Để chuẩn bị cho kì thi học kì 2 lớp 9 sắp tới, các em học sinh cần ôn tập theo đề cương, bên cạnh đó cần thực hành luyện đề để làm quen với nhiều dạng đề khác nhau cũng như nắm được cấu trúc đề thi. Chuyên mục Đề thi học kì 2 lớp 9 trên VnDoc tổng hợp đề thi của tất cả các môn, là tài liệu phong phú và hữu ích cho các em ôn tập và luyện đề. Đây cũng là tài liệu hay cho thầy cô tham khảo ra đề. Mời thầy cô và các em tham khảo.