Đề thi Olympic Toán sinh viên Đại học Sư Phạm TP HCM năm 2013

ĐẠI HỌC SƯ PHẠM THÀNH PHỐ HỒ CHÍ MINH

KỲ THI OLYMPIC TOÁN SINH VIÊN 2013 MÔN: TOÁN HỌC

MÔN THI: GIẢI TÍCH

Câu 1:

Cho |q| < 1 và lim_n-→∞ ε_n = 0

Giả sử dãy (a_n) không âm và thoả mãn: a_n1 ≤ qa_nε_n, với mọi n thuộc N

Chứng minh: lim_n→∞ a_n = 0

Câu 2: Giả sử hai dãy (a_n), (b_n) thoả các điều kiện sau: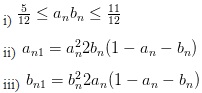

Tìm lim_n→∞ a_n; lim_n→∞ b_n

Câu 3:

Cho P(x),Q(x) là các đa thức hệ số thực thoả mãn:

P[e^xxQ(x)x²Q²(x)] = Q[e^xxP(x)x²P²(x)], với mọi x thuộc R

Chứng minh P ≡ Q

Câu 4:

Cho f liên tục trên [a;b], khả vi trên (a,b) và f'(x) # 0 với mọi x thuộc (a, b)

Chứng minh rằng:

Câu 5: Cho a₁, a₂,...., a₂₀₁₃; b₁, b₂, ..., b₂₀₁₃ > 0 sao cho: a^x₁a^x₂...a^x₂₀₁₃ ≥ b^x₁b^x₂...b^x₂₀₁₃, với mọi x thuộc R

Xét tính đơn điệu của hàm số:

Câu 6: Cho f thuộc C2[0; a], a > 0, f(x) ≥ 0, f''(x) ≥ 0, với mọi x thuộc [0; a]

Giả sử f(0) = f(a) = 1. Gọi m = min_{[0; a]}f(x), chứng minh:

MÔN THI: ĐẠI SỐ

Bài 1: Cho A là ma trận cấp 2 × 3 và B là ma trận cấp 3 × 2 thỏa:

Tìm AB

Bài 2: Cho n là số nguyên dương, x, a, b là các số thực với a # b. Ký hiệu M_n là ma trận vuông cấp 2n thỏa:

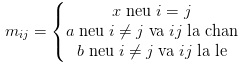
Tìm:

Bài 3: Cho A thuộc M_n(R). Chứng minh rằng A^tA và A^t có cùng hạng.

Bài 4: Cho ma trận A như sau với bi # 0, với mọi i thuộc {1; 2; ... ; n}

Chứng minh rằng (A) ≥ n - 1

Bài 5:

a) Cho x1, ..., xn là n vector khác không của kgvt V và φ: V → V là một phép biến đổi tuyến tính thỏa φx₁ = x₂, φx_k = x_k - x_k-1 với k = 2,3,…,n

Chứng minh rằng hệ vector x₁,..., x_n độc lập tuyến tính.

b) Chứng minh rằng hệ vector {|x - 1|, |x - 2|, ..., |x - n|} độc lập tuyến tính trong không gian các hàm số liên tục trên R

Bài 6:

Cho A,B là hai ma trận đối xứng cấp n. Giả sử tồn tại hai ma trận X,Y cấp n thỏa det(AXBY) # 0. Chứng minh det(A²B²) # 0

Bài 7:

Cho A, B, C, D thuộc M_n(R) thỏa ABt và CDt là hai ma trận đối xứng và AD^t - BC^t = I. Chứng minh rằng: A^tD - C^tB = I

Bài 8:

Cho P,Q,U,V là các ma trận cấp 2 thỏa U,V là 2 nghiệm phân biệt của phương trình X² - PXQ = 0 và U-V khả nghịch.

Chứng minh Tr(UV) = Tr(P) và det(UV) = det(Q)

Bài 9: Cho P là đa thức hệ số thực có n nghiệm thực phân biệt lớn hơn 1. Xét Q(x) = (x²1)P(x)P'(x)x(P²(x)P'²(x))

Q(x) có ít nhất 2n-1 nghiệm thực phân biệt đúng hay sai?