Đề thi thử THPT Quốc gia môn Toán năm 2016 trường THPT B Nghĩa Hưng, Nam Định (Lần 2)

Đề thi thử THPT Quốc gia môn Toán năm 2016

Đề thi thử THPT Quốc gia môn Toán năm 2016 trường THPT B Nghĩa Hưng, Nam Định (Lần 2) là đề thi thử Quốc gia năm 2016a môn Toán có đáp án. Tài liệu này giúp các bạn tự luyện tập, ôn luyện lại kiếm thức đã học, nhằm chuẩn bị tốt nhất cho các kì thi quan trọng sắp tới. Mời các bạn tham khảo.

Đề thi thử THPT Quốc gia môn Toán năm 2016 trường THPT Thanh Hà, Hải Dương (Lần 3)

Đề thi thử THPT Quốc gia môn Toán lần 1 năm 2016 trường THPT Chuyên Vĩnh Phúc

SỞ GD – ĐT NAM ĐỊNH TRƯỜNG THPT B NGHĨA HƯNG ĐỀ CHÍNH THỨC

ĐỀ THI THỬ LẦN II KỲ THI THPT QUỐC GIA NĂM HỌC 2015 -2016 MÔN TOÁN (Thời gian 180 phút, đề thi gồm 01 trang)

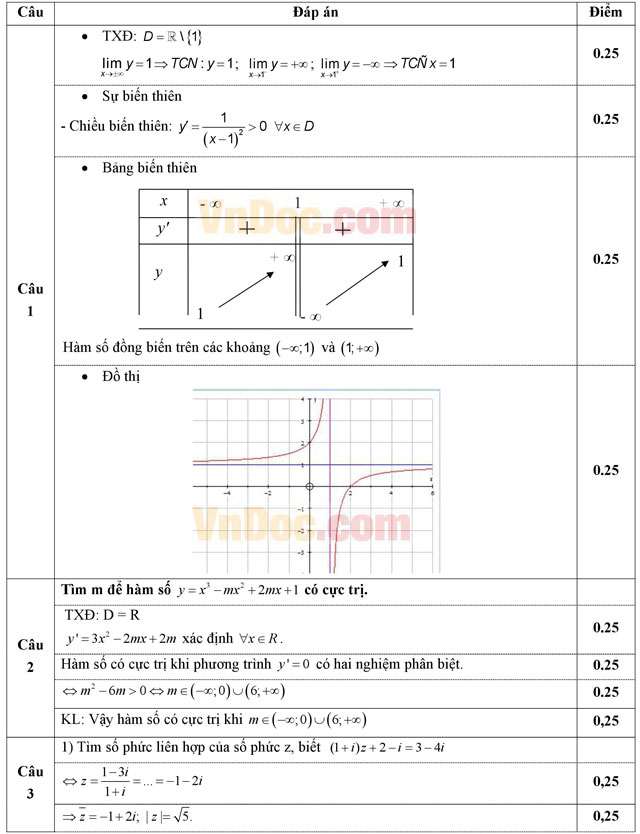
Câu 1 (1,0 điểm). Khảo sát và vẽ đồ thị (C) của hàm số .

Câu 2 (1,0 điểm). Tìm m để hàm số y = x³ - mx² + 2mx + 1 có cực trị.

Câu 3 (1,0 điểm).

1. Tìm số phức liên hợp và mô đun của số phức z biết (1 + i)z + 2 - i = 3 - 4i.
2. Giải phương trình:

Câu 4 (1,0 điểm). Tính tích phân .

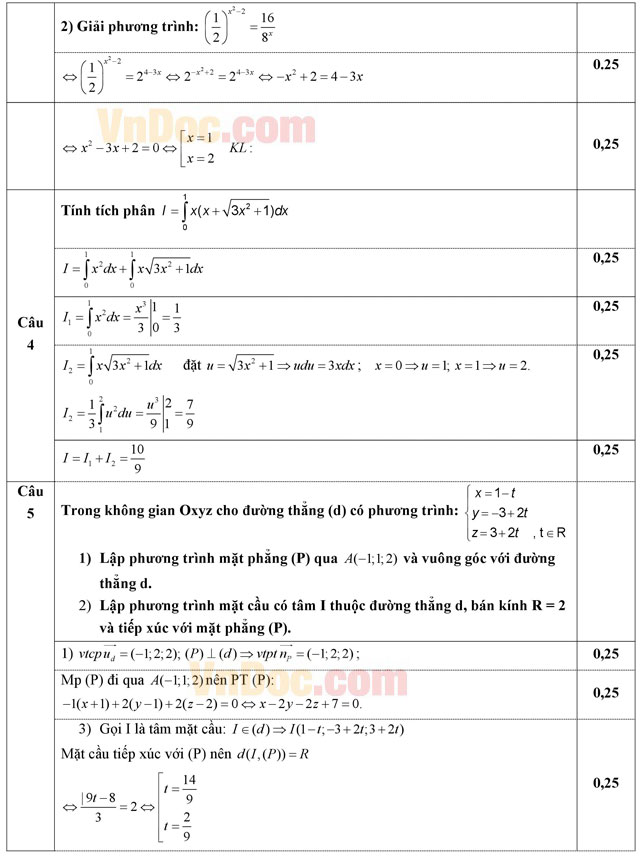
Câu 5 (1,0 điểm). Trong không gian Oxyz cho đường thẳng (d) có phương trình: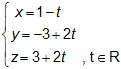

1. Lập phương trình mặt phẳng (P) qua A(-1; 1; 2) và vuông góc với đường thẳng d.
2. Lập phương trình mặt cầu có tâm I thuộc đường thẳng d, bán kính R = 2 và tiếp xúc với mặt phẳng (P).

Câu 6 (1,0 điểm).

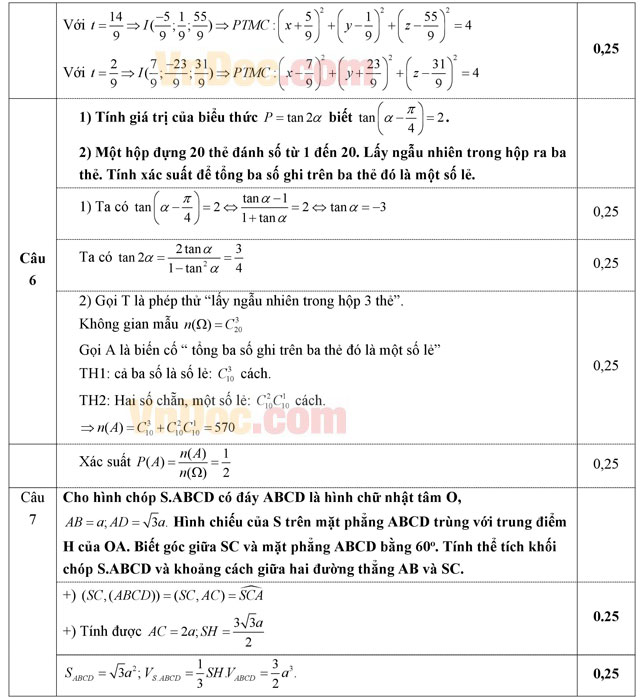
1. Tính giá trị của biểu thức P = tan2α biết .
2. Một hộp đựng 20 thẻ đánh số từ 1 đến 20. Lấy ngẫu nhiên trong hộp ra ba thẻ. Tính xác suất để tổng ba số ghi trên ba thẻ đó là một số lẻ.

Câu 7 (1,0 điểm). Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật tâm O, AB = a, AD = √3a. Hình chiếu của S trên mặt phẳng (ABCD) trùng với trung điểm H của OA. Biết góc giữa SC và mặt phẳng (ABCD) bằng 60^o. Tính thể tích khối chóp S.ABCD và khoảng cách giữa hai đường thẳng AB và SC theo a (a>0).

Câu 8 (1,0 điểm). Cho tam giác ABC vuông tại A, AH là đường cao. Gọi M là điểm thuộc đoạn HC (M không trùng với H, C); E, K lần lượt là hình chiếu của B, C trên đường thẳng AM. Biết H(2; 2), K(3; 1), A thuộc đường thẳng d₁: 2x - y - 2 = 0, E thuộc đường thẳng d₂: x + y - 6 = 0. Tìm tọa độ các điểm A, B, C.

Câu 9 (1,0 điểm). Giải hệ phương trình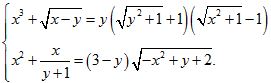

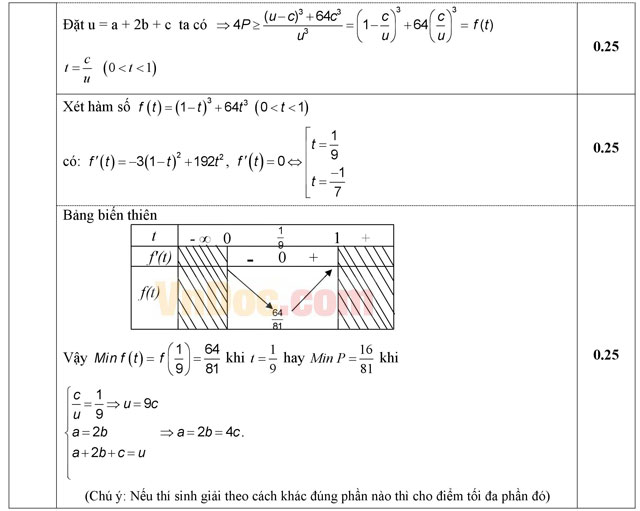
Câu 10 (1,0 điểm). Cho ba số thực dương a, b, c. Tìm giá trị nhỏ nhất của biểu thức .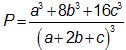

Đáp án đề thi thử THPT Quốc gia môn Toán năm 2016