Đề thi thử THPT Quốc gia năm 2016 môn Toán trường THCS&THPT Alfred Nobel

Đề thi thử THPT Quốc gia năm 2016 môn Toán

Đề thi thử THPT Quốc gia năm 2016 môn Toán trường THCS&THPT Alfred Nobel là đề thi thử Đại học môn Toán năm 2016 hữu ích dành cho các bạn học sinh lớp 12, những bạn chuẩn bị bước vào kì thi THPT Quốc gia môn Toán luyện đề, củng cố kiến thức nhằm đạt két quả tốt nhất trong kỳ thi quan trọng sắp diễn ra.

Đề thi thử THPT Quốc gia năm 2016 môn Toán trường THPT Nguyễn Văn Trỗi, Hà Tĩnh

Đề thi thử THPT Quốc gia năm 2016 môn Toán trường THPT Chuyên Khoa học Tự nhiên, Hà Nội (Lần 5)

TRƯỜNG THCS&THPT ALFRED NOBEL

ĐỀ THI THỬ KỲ THI TRUNG HỌC PHỔ THÔNG QUỐC GIA NĂM 2016 Môn thi: TOÁN Thời gian làm bài: 180 phút, không kể thời gian phát đề

Câu 1 (1,0 điểm). Khảo sát sự biến thiên và vẽ đồ thị hàm số y = -x⁴ + 2x².

Câu 2 (1,0 điểm). Cho hàm số có đồ thị (C). Viết phương trình tiếp tuyến của đồ thị (C) tại giao điểm của đồ thị (C) với đường thẳng d có phương trình y = 2x - 5.

Câu 3 (1,0 điểm).

a) Trên tập hợp số phức, gọi z₁, z₂ là hai nghiệm của phương trình z² + 2z + 5 = 0. Tìm z₁, z₂ và tính môđun của số phức w = z₁ + z₁ + 1 - 3i.

b) Giải phương trình: 2^x+1 + 3.2^-x - 7 = 0.

Câu 4 (1,0 điểm). Tính tích phân sau: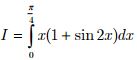

Câu 5 (1,0 điểm). Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P): 2x + y - 2z + 5 = 0 và điểm I(1;2;3). Viết phương trình mặt cầu (S) tâm I và tiếp xúc với mặt phẳng (P). Tìm tọa độ tiếp điểm H của mặt cầu (S) và mặt phẳng (P).

Câu 6 (1,0 điểm).

a) Giải phương trình: cos2x + cosx - 2 = 0.

b) Gọi S là tập hợp các số tự nhiên có 4 chữ số đôi một khác nhau được thành lập từ các chữ số 0, 1, 2, 3, 4, 5. Chọn ngẫu nhiên một số từ tập S. Tính xác suất để số được chọn là số chẵn.

Câu 7 (1,0 điểm). Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm I và có cạnh bằng a. Góc BAD = 60^o. Hình chiếu vuông góc của S lên mặt phẳng (ABCD) là trung điểm H của IA. Góc giữa SC và mặt phẳng (ABCD) bằng 45^o. Tính theo a thể tích của khối chóp S.ABCD và khoảng cách giữa hai đường thẳng AB và SD.

Câu 8 (1,0 điểm). Trong mặt phẳng với hệ tọa độ Oxy, cho tam giác ABC cân tại A có A(2;1);B(-3;-3), trực tâm H(1;-1). Viết phương trình đường thẳng chứa cạnh AC của tam giác ABC.

Câu 9 (1,0 điểm). Giải phương trình: .

Câu 10 (1,0 điểm). Cho a, b, c là các số thực dương và thỏa mãn điều kiện a² + b² + c² = 3. Tìm giá trị nhỏ nhất của biểu thức:

——— Hết ———

Thí sinh không được sử dụng tài liệu. Cán bộ coi thi không giải thích gì thêm!