Đề thi thử THPT Quốc gia năm 2016 môn Toán trường THPT Chuyên Khoa học Tự nhiên, Hà Nội (Lần 1)

Đề thi thử THPT Quốc gia năm 2016 môn Toán

Đề thi thử THPT Quốc gia năm 2016 môn Toán trường THPT Chuyên Khoa học Tự nhiên, Hà Nội (Lần 1) gồm 10 câu hỏi, là tài liệu ôn tập THPT Quốc gia môn Toán năm 2016 hữu ích dành cho các bạn học sinh, giúp các bạn chuẩn bị tốt nhất cho bài thi sắp tới.

Đề thi thử THPT Quốc gia môn Toán lần 1 năm 2016 trường THPT Chuyên Vĩnh Phúc

Đề thi thử THPT Quốc gia năm 2016 môn Hóa học trường THPT Chuyên Khoa học Tự nhiên, Hà Nội (Lần 1)

Đề thi thử THPT Quốc gia năm 2016 môn Vật lý trường THPT Chuyên Khoa học Tự nhiên, Hà Nội (Lần 1)

TRƯỜNG ĐẠI HỌC KHTN TRƯỜNG THPT CHUYÊN KHTN

ĐỀ THI THỬ THPT QG LẦN 1 NĂM HỌC 2015 - 2016 Môn: TOÁN Thời gian làm bài: 180 phút

Câu 1 (1,0 điểm). Khảo sát sự biến thiên và vẽ đồ thị của hàm số y = x⁴ −2x².

Câu 2 (1,0 điểm). Viết phương trình tiếp tuyến của đồ thị hàm số biết tiếp tuyến cắt trục Ox, Oy lần lượt tại các điểm A, B thoả mãn điều kiện OB = 3OA.

Câu 3 (1,0 điểm).

a) Tìm phần thực và phần ảo của số phức z thoả mãn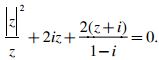

b) Giải phương trình trên tập số thực: (3− √5)^x +(3+ √5)^x = 2^x+1.

Câu 4 (1,0 điểm). Tính tích phân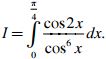

Câu 5 (1,0 điểm). Trong không gian với hệ toạ độ Oxyz cho mặt phẳng (P): x + 2y + z−4 = 0 và đường thẳng . Tìm toạ độ giao điểm A của đường thẳng d và mặt phẳng (P) và viết phương trình đường thẳng Δnằm trong mặt phẳng (P) đồng thời cắt và vuông góc với đường thẳng d.

Câu 6 (1,0 điểm).

a) Giải phương trình lượng giác: sin x− √3sin 2x = √3 cosx + cos2x.

b) Xét 1 đa giác đều 12 cạnh, hỏi có bao nhiêu tam giác không cân có ba đỉnh là các đỉnh của đa giác đã cho?

Câu 7 (1,0 điểm). Cho hình chóp S.ABC có đáy ABC là tam giác cân tại A trong đó AB = AC = a,BAC ! =1200 ; mặt bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Tính theo a thể tích khối chóp S.ABC và bán kính mặt cầu ngoại tiếp khối chóp S.ABC.

Câu 8 (1,0 điểm). Trong mặt phẳng toạ độ Oxy, cho tam giác ABC có A(4; 6), trực tâm H(4; 4), trung điểm M của cạnh BC thuộc đường thẳng Δ: x − 2y − 1 = 0. Gọi E, F lần lượt là chân đường cao hạ từ các đỉnh B, C của tam giác. Tìm toạ độ các đỉnh B, C biết rằng đường thẳng EF song song với đường thẳng d: x−3y + 5 = 0.

Câu 9 (1,0 điểm). Giải hệ phương trình trên tập số thực: .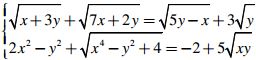

Câu 10 (1,0 điểm). Xét các số thực dương x, y, z thoả mãn x² + y³ + z⁴ ≥ x³ + y⁴ + z⁵. Chứng minh rằng: x³ + y³ + z³ ≤ 3.

---Hết---