Đề thi tuyển sinh lớp 10 THPT chuyên Tin học tỉnh Thái Nguyên năm 2012 - 2013 môn Toán - Có đáp án

Nhằm giúp các bạn chuẩn bị thật tốt kiến thức để làm bài thi đạt hiệu quả cao, Vndoc.com xin giới thiệu: Đề thi tuyển sinh lớp 10 THPT chuyên Tin học tỉnh Thái Nguyên năm 2012 - 2013 môn Toán - Có đáp án.

Đề thi tuyển sinh lớp 10 (chuyên Tin) môn Toán:

SỞ GIÁO DỤC VÀ ĐÀO TẠO TỈNH THÁI NGUYÊN (ĐỀ THI CHÍNH THỨC)

ĐỀ THI TUYỂN SINH LỚP 10 THPT CHUYÊN NĂM HỌC 2012 - 2013 MÔN THI: TOÁN (Chuyên Tin học) Thời gian làm bài: 150 phút (không kể thời gian giao đề)

Câu 1 (2,0 điểm)

Cho biểu thức: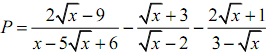

a. Rút gọn P.

b. Tìm các giá trị nguyên của x để giá trị của biểu thức P là số nguyên.

Câu 2 (2,0 điểm)

Cho phương trình: x² - 2(m - 1)x + m - 3 = 0 (1)

a. Chứng minh rằng với mọi m thuộc R phương trình (1) luôn có hai nghiệm phân biệt x₁, x₂.

b. Tìm các giá trị của m để x₁² + x₂² đạt giá trị nhỏ nhất.

Câu 3 (3,0 điểm)

a. Tìm nghiệm nguyên của phương trình: 3x² - 2xy + y - 5x + 2 = 0

b. Trong một hộp có 2012 viên sỏi. Hai người A và B tham gia trò chơi bốc sỏi như sau: Mỗi người lần lượt phải bốc ít nhất 1 viên và nhiều nhất 30 viên sỏi. Người nào bốc được viên sỏi cuối cùng sẽ thắng cuộc. Hỏi ai luôn thắng cuộc và chỉ ra thuật chơi.

Câu 4 (1 điểm)

Từ 1 đến 2013 có bao nhiêu số tự nhiên biểu diễn được dưới dạng hiệu bình phương của hai số nguyên (dạng a² - b²).

Câu 5 (2 điểm)

Cho tam giác ABC, lấy điểm M nằm trong tam giác ABC, các đường thẳng AM, BM, CM cắt các cạnh BC, CA, AB tương ứng tại A', B', C'.

a. Chứng minh rằng:
b. Tìm giá trị nhỏ nhất của biểu thức: