Đề thi tuyển sinh lớp 10 THPT Chuyên tỉnh Thái Nguyên năm 2012 - 2013 môn Toán - Có đáp án
Vndoc.com xin giới thiệu đến các bạn lớp 9, chuẩn bị thi lên lớp 10: Đề thi tuyển sinh lớp 10 THPT Chuyên tỉnh Thái Nguyên năm 2012 - 2013 môn Toán - Có đáp án.
Đề thi tuyển sinh lớp 10 môn Toán:
SỞ GIÁO DỤC VÀ ĐÀO TẠO | ĐỀ THI TUYỂN SINH LỚP 10 THPT CHUYÊN |
Bài 1 (1,5 điểm)
Chứng minh: 1.2.3….1005.1006.1007 + 1008.1009….2013.2014 chia hết cho 2015
Bài 2 (1,5 điểm)
Chứng minh rằng phương trình 2013x2 + 2 = y2 không có nghiệm nguyên.
Bài 3 (1 điểm)
Kí hiệu [x] dùng để chỉ số nguyên lớn nhất không vượt quá x. Ví dụ [3,47] = 3; [5] = 5; [ -2,75] = -3 …
Hãy giải phương trình: 
Bài 4 (2 điểm)
Cho biểu thức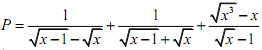 
a. Tìm x để P > 0
b. Tìm giá trị của P khi 
Bài 5 (1 điểm)
Ta viết dãy phân số 
Hỏi phân số 
đứng ở vị trí thứ bao nhiêu trong dãy trên.
Bài 6 (1,5 điểm)
Cho hình chữ nhật ABCD nội tiếp trong một đường tròn. Gọi K là một điểm tùy ý trên cung nhỏ AD (K không trùng với A hoặc D), gọi K1, K2, K3, K4 lần lượt là chân các đường vuông góc hạ từ K xuống AD, AB, CD, CB. Chứng minh K1 là trực tâm của tam giác K2K3K4.
Bài 7 (1,5 điểm)
Trong hình tròn tâm O, bán kính R dựng hai đường kính vuông góc AE và BF. Trên cung nhỏ EF lấy điểm C. Gọi P là giao điểm của AC và BF, gọi Q là giao điểm của AE và CB. Chứng minh diện tích của tứ giác APQB bằng R2.
