Giải Toán 8 bài 5: Những hằng đẳng thức đáng nhớ (tiếp)

Giải SGK Toán 8 trang 16

Toán 8 bài 5: Những hằng đẳng thức đáng nhớ (tiếp)

A. Kiến thức cơ bản về hằng đẳng thức đáng nhớ phần tiếp theo:
B. Trả lời câu hỏi trang 14, 15 SGK Toán 8 tập 1
C. Giải bài tập Toán 8 trang 16
D. Giải bài tập Toán 8 trang 16, 17 tập 1: Luyện tập

Giải Toán 8 trang 16 SGK Toán lớp 8 tập 1: Những hằng đẳng thức đáng nhớ (tiếp) tổng hợp câu hỏi và lời giải chi tiết, rõ ràng theo khung chương trình sách giáo khoa Toán lớp 8. Lời giải hay bài tập Toán 8 gồm các bài giải tương ứng với từng bài tập trong SGK, giúp các em học sinh ôn tập và củng cố các dạng bài tập, rèn kỹ năng giải Toán 8 hiệu quả.

A. Kiến thức cơ bản về hằng đẳng thức đáng nhớ phần tiếp theo:

6. Tổng hai lập phương: A³ + B³ = (A + B)(A² – AB + B²)

7. Hiệu hai lập phương: A³ – B³ = (A – B)(A² + AB + B²)

Ta có 7 hằng đẳng thức đáng nhớ:

1. (A + B)² = A² + 2AB + B²

2. (A – B)² = A² – 2AB + B²

3. A2 – B2 = (A + B)(A – B)

4. (A + B)³ = A³ + 3A²B + 3AB² + B³

5. (A – B)³ = A³ – 3A²B + 3AB² – B³

6. A³ + B³ = (A + B)(A² – AB + B²)

7. A³ – B³ = (A – B)(A² + AB + B²)

B. Trả lời câu hỏi trang 14, 15 SGK Toán 8 tập 1

Câu hỏi 1 trang 14 SGK Toán 8 tập 1

Tính $\left( {a + b} \right)\left( {{a^2} - ab + {b^2}} \right)$ $\left( {a + b} \right)\left( {{a^2} - ab + {b^2}} \right)$ (Với a, b là các số tùy ý).

$\eqalign{ & \left( {a + b} \right)({a^2} - ab + {b^2}) \cr & = a({a^2} - ab + {b^2}) + b({a^2} - ab + {b^2}) \cr & = a.{a^2} + a.\left( { - ab} \right) + a.{b^2} + b.{a^2} + b.\left( { - ab} \right) + b.{b^2} \cr & = {a^3} - {a^2}b + a{b^2} + {a^2}b - a{b^2} + {b^3} \cr & = {a^3} + \left( {{a^2}b - {a^2}b} \right) + \left( {a{b^2} - a{b^2}} \right) + {b^3} \cr & = {a^3} + {b^3} \cr}$ $\eqalign{ & \left( {a + b} \right)({a^2} - ab + {b^2}) \cr & = a({a^2} - ab + {b^2}) + b({a^2} - ab + {b^2}) \cr & = a.{a^2} + a.\left( { - ab} \right) + a.{b^2} + b.{a^2} + b.\left( { - ab} \right) + b.{b^2} \cr & = {a^3} - {a^2}b + a{b^2} + {a^2}b - a{b^2} + {b^3} \cr & = {a^3} + \left( {{a^2}b - {a^2}b} \right) + \left( {a{b^2} - a{b^2}} \right) + {b^3} \cr & = {a^3} + {b^3} \cr}$

Câu hỏi 2 trang 15 SGK Toán 8 tập 1

Phát biểu hằng đẳng thức (6) bằng lời.

Áp dụng

a) Viết ${x^3} + 8$ ${x^3} + 8$ dưới dạng tích.

b) Viết $\left( {x + 1} \right)\left( {{x^2} - x + 1} \right)$ $\left( {x + 1} \right)\left( {{x^2} - x + 1} \right)$ dưới dạng tổng.

Đáp án

Phát biểu hằng đẳng thức (6): Tổng của lập phương hai biểu thức bằng tích của tổng hai biểu thức và bình phương thiếu của hiệu hai biểu thức đó

Áp dụng:

$\begin{array}{l} a)\,{x^3} + 8 = {x^3} + {2^3}\\ = \left( {x + 2} \right)\left( {{x^2} - 2x + {2^2}} \right)\\ = \left( {x + 2} \right)\left( {{x^2} - 2x + 4} \right)\\ b)\,\left( {x + 1} \right)\left( {{x^2} - x + 1} \right)\\ = \left( {x + 1} \right)\left( {{x^2} - x.1 + {1^2}} \right)\\ = {x^3} + {1^3} = {x^3} + 1 \end{array}$ $\begin{array}{l} a)\,{x^3} + 8 = {x^3} + {2^3}\\ = \left( {x + 2} \right)\left( {{x^2} - 2x + {2^2}} \right)\\ = \left( {x + 2} \right)\left( {{x^2} - 2x + 4} \right)\\ b)\,\left( {x + 1} \right)\left( {{x^2} - x + 1} \right)\\ = \left( {x + 1} \right)\left( {{x^2} - x.1 + {1^2}} \right)\\ = {x^3} + {1^3} = {x^3} + 1 \end{array}$

Câu hỏi 3 trang 15 SGK Toán 8 tập 1

Tính $\left( {a - b} \right)\left( {{a^2} + ab + {b^2}} \right)$ $\left( {a - b} \right)\left( {{a^2} + ab + {b^2}} \right)$ (với a, b là các số tùy ý)

Đáp án

$\eqalign{ & \left( {a - b} \right)\left( {{a^2} + ab + {b^2}} \right) \cr & = a\left( {{a^2} + ab + {b^2}} \right) - b\left( {{a^2} + ab + {b^2}} \right) \cr & = a.{a^2} + a.ab + a.{b^2} + \left( { - b} \right).{a^2} + \left( { - b} \right).ab + \left( { - b} \right).{b^2} \cr & = {a^3} + {a^2}b + a{b^2} - {a^2}b - a{b^2} - {b^3} \cr & = {a^3} + \left( {{a^2}b - {a^2}b} \right) + \left( {a{b^2} - a{b^2}} \right) - {b^3} \cr & = {a^3} - {b^3} \cr}$ $\eqalign{ & \left( {a - b} \right)\left( {{a^2} + ab + {b^2}} \right) \cr & = a\left( {{a^2} + ab + {b^2}} \right) - b\left( {{a^2} + ab + {b^2}} \right) \cr & = a.{a^2} + a.ab + a.{b^2} + \left( { - b} \right).{a^2} + \left( { - b} \right).ab + \left( { - b} \right).{b^2} \cr & = {a^3} + {a^2}b + a{b^2} - {a^2}b - a{b^2} - {b^3} \cr & = {a^3} + \left( {{a^2}b - {a^2}b} \right) + \left( {a{b^2} - a{b^2}} \right) - {b^3} \cr & = {a^3} - {b^3} \cr}$

Câu hỏi 4 trang 15 SGK Toán 8 tập 1

Phát biểu hằng đẳng thức (7) bằng lời:

Áp dụng

a) Tính $\left( {x - 1} \right)\left( {{x^2} + x + 1} \right)$ $\left( {x - 1} \right)\left( {{x^2} + x + 1} \right)$

b) Viết $8{x^3} - {y^3}$ $8{x^3} - {y^3}$ dưới dạng tích

c) Hãy đánh dấu x vào ô có đáp số đúng của tích: $\left( {x + 2} \right)\left( {{x^2} - 2x + 4} \right)$ $\left( {x + 2} \right)\left( {{x^2} - 2x + 4} \right)$

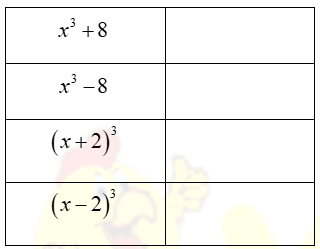
Câu hỏi 4 trang 15 SGK Toán 8 tập 1

Đáp án:

Phát biểu hằng đẳng thức số (7): Hiệu của lập phương hai biểu thức bằng tích của hiệu hai biểu thức và bình phương thiếu của tổng hai biểu thức đó

a) $\left( {x - 1} \right)\left( {{x^2} + x + 1} \right) = {x^3} - {1^3} = {x^3} - 1$ $\left( {x - 1} \right)\left( {{x^2} + x + 1} \right) = {x^3} - {1^3} = {x^3} - 1$

b) $8{x^3} - {y^3} = {\left( {2x} \right)^3} - {y^3} = \left( {2x - y} \right)\left( {4{x^2} + 2xy + {y^2}} \right)$ $8{x^3} - {y^3} = {\left( {2x} \right)^3} - {y^3} = \left( {2x - y} \right)\left( {4{x^2} + 2xy + {y^2}} \right)$

c) $\left( {x + 2} \right)\left( {{x^2} - 2x + 4} \right) = {x^3} + 8$ $\left( {x + 2} \right)\left( {{x^2} - 2x + 4} \right) = {x^3} + 8$

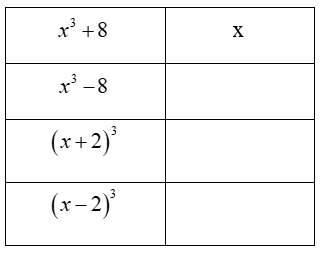
Câu hỏi 4 trang 15 SGK Toán 8 tập 1

C. Giải bài tập Toán 8 trang 16

Bài 30 trang 16 SGK Toán 8 Tập 1

Rút gọn các biểu thức sau:

a) (x + 3)(x² – 3x + 9) – (54 + x³)

b) (2x + y)(4x² – 2xy + y²) – (2x – y)(4x² + 2xy + y²)

Đáp án:

a) (x + 3)(x² – 3x + 9) – (54 + x³) = (x + 3)(x² – 3x + 3²) – (54 + x³)

= x³ + 3³ – (54 + x³)

= x³ + 27 – 54 – x³

= -27

b) (2x + y)(4x² – 2xy + y²) – (2x – y)(4x² + 2xy + y²)

= (2x + y)[(2x)² – 2 . x . y + y2] – (2x – y)(2x)² + 2 . x . y + y²]

= [(2x)³ + y³]- [(2x)³ – y³]

= (2x)³ + y³– (2x)³ + y³= 2y³

Bài 31 trang 16 SGK Toán 8 Tập 1

Chứng minh rằng:

a) a³ + b³ = (a + b)³ – 3ab(a + b)

b) a³ – b³ = (a – b)³ + 3ab(a – b)

Áp dụng: Tính a³ + b³, biết a . b = 6 và a + b = -5

Đáp án:

a) a³ + b³ = (a + b)³ – 3ab(a + b)

Thực hiện vế phải:

(a + b)³ – 3ab(a + b) = a³ + 3a²b+ 3ab² + b³ – 3a²b – 3ab²

= a³ + b³

Vậy a³ + b³= (a + b)³ – 3ab(a + b)

b) a³ – b³ = (a – b)³ + 3ab(a – b)

Thực hiện vế phải:

(a – b)³ + 3ab(a – b) = a³ – 3a²b+ 3ab² – b³ + 3a²b – 3ab²

= a³ – b³

Vậy a³ – b³ = (a – b)³ + 3ab(a – b)

Áp dụng:

Với ab = 6, a + b = -5, ta được:

a³ + b³ = (a + b)³ – 3ab(a + b) = (-5)³ – 3 . 6 . (-5)

= -5³ + 3.6.5 = -125 + 90 = -35.

Bài 32 trang 16 SGK Toán 8 Tập 1

Điền các đơn thức thích hợp vào ô trống:

a) (3x + y)(☐-☐+☐) = 27x³ + y³

b) (2x -☐)(☐- 10x +☐) = 8x³ -125

Đáp án:

a) Ta có: 27x³ + y³ = (3x)³ + y³= (3x + y)[(3x)² – 3x.y + y²] = (3x + y)(9x² – 3xy + y²)

Nên: (3x + y) (9x² – 3xy + y²) = 27x³ + y³

b) Ta có: 8x³ – 125 = (2x)³ – 5³= (2x – 5)[(2x)² + 2x . 5 + 5²]

= (2x – 5)(4x² + 10x + 25)

Nên: (2x – 5)(4x² + 10x + 25)= 8x³ – 125

D. Giải bài tập Toán 8 trang 16, 17 tập 1: Luyện tập

Bài 33 trang 16 SGK Toán 8 Tập 1

a) (2 + xy)² b) (5 – 3x)²

c) (5 – x²)(5 + x²) d) (5x – 1)³

e) (2x – y)(4x² + 2xy + y²) f) (x + 3)(x² – 3x + 9)

Đáp án:

a) (2 + xy)2 = 2² + 2.2.xy + (xy)² = 4 + 4xy + x²y²

b) (5 – 3x)²= 5² – 2.5.3x + (3x)² = 25 – 30x + 9x²

c) (5 – x²)(5 + x²) = 5² – (x²)² = 25 – x⁴

d) (5x – 1)³ = (5x)³ – 3.(5x)². 1 + 3.5x.1² – 1³ = 125x³ – 75x² + 15x – 1

e) (2x – y)(4x² + 2xy + y²) = (2x – y)[(2x)² + 2x . y + y²] = (2x)³ – y³ = 8x³ – y³

f) (x + 3)(x² – 3x + 9) = (x + 3)(x² – 3x + 3²) = x3 + 3³ = x³ + 27.

Bài 34 trang 17 SGK Toán 8 Tập 1

Rút gọn các biểu thực sau:

a) (a + b)² – (a – b)²; b) (a + b)³ – (a – b)³ – 2b³

c) (x + y + z)² – 2(x + y + z)(x + y) + (x + y)²

Đáp án:

a) (a + b)² – (a – b)² = (a² + 2ab + b²) – (a² – 2ab + b²)

= a2 + 2ab + b² – a² + 2ab – b²= 4ab

Hoặc (a + b)² – (a – b)² = [(a + b) + (a – b)][(a + b) – (a – b)]

= (a + b + a – b)(a + b – a + b) = 2a . 2b = 4ab

b) (a + b)³ – (a – b)³ – 2b³

= (a³ + 3a²b + 3ab² + b³) – (a³ – 3a²b + 3ab² – b³) – 2b³

= a³ + 3a²b + 3ab² + b³– a³ + 3a²b – 3ab² + b³ – 2b³= 6a²b

Hoặc (a + b)³ – (a – b)³ – 2b³ = [(a + b)³ – (a – b)³] – 2b³

= [(a + b) – (a – b)][(a + b)² + (a + b)(a – b) + (a – b)²] – 2b³

= (a + b – a + b)(a² + 2ab + b² + a² – b² + a² – 2ab + b²) – 2b³

= 2b.(3a² + b²) – 2b³ = 6a²b + 2b³ – 2b3 = 6a²b

c) (x + y + z)² – 2(x + y + z)(x + y) + (x + y)²

= x² + y² + z²+ 2xy + 2yz + 2xz – 2(x² + xy + yx + y² + zx + zy) + x² + 2xy + y²

= 2x² + 2y² + z² + 4xy + 2yz + 2xz – 2x²– 4xy – 2y²– 2xz – 2yz = z²

Bài 35 trang 17 SGK Toán 8 Tập 1

Tính nhanh:

a) 34² + 66² + 68 . 66; b) 74² + 24²– 48 . 74.

Đáp án:

a) 34²+ 66² + 68 . 66 = 34²+ 2.34.66 + 66² = (34 + 66)2 = 100² = 10000.

b) 74² + 24² – 48.74 = 74² – 2.74.24 + 24² = (74 – 24)²= 50² = 2500

Bài 36 trang 17 SGK Toán 8 Tập 1

Tính giá trị của biểu thức:

a) x² + 4x + 4 tại x = 98; b) x³ + 3x² + 3x + 1 tại x = 99

Đáp án:

a) x² + 4x + 4 = x² + 2.x.2 + 2² = (x+ 2)²

Với x = 98: (98+ 2)2 =1002 = 10000

b) x³+ 3x² + 3x + 1 = x³ + 3.1.x² + 3.x .1²+ 1³ = (x + 1)³

Với x = 99: (99+ 1)³ = 100³ = 1000000

Bài 37 trang 17 SGK Toán 8 Tập 1

Dùng bút chì nối các biểu thức sao cho chúng tạo thành hai vế của một hằng đẳng thức (theo mẫu)

(x-y)(x²+xy +y²)

(x+y)(x-y)

x² – 2xy + y²

(x +y)²

(x +y)(x² –xy +2)

y³ + 3xy² + 3x²y + x³

(x-y)³

x³ + y³

x³ – y³

x² + 2xy + y²

x² – y²

(y-x)²

x³ – 3x²y + 3xy² – y³

(x+y)³

Đáp án:

Ta có: (x – y)(x² + xy + y²) = X³ – y³ và (x + y)(x² – xy + y²) = X³ + y³

(x + y) (x – y) = X² – y² và X² – 2xy + y² = (x – y)² = (y – x)² y³ + 3xy² + 3x²y + X³ = (y + x)³ = (x + y)³ và (x + y)² = X² + 2xy + y² (x – y)³ = X³ – 3x²y + 3xy² – y³

Từ đó ta có:

Bài 37

Bài 38 trang 17 SGK Toán 8 Tập 1

Chứng minh các đẳng thức sau:

a) (a – b)³ = -(b – a)³; b) (- a – b)² = (a + b)²

Đáp án:

a) (a – b)³ = -(b – a)³

Biến đổi vế phải thành vế trái:

-(b – a)³= -(b³ – 3b²a + 3ba² – a³) = – b³ + 3b²a – 3ba² + a³

= a³ – 3a²b + 3ab² – b³ = (a – b)³

Sử dụng tính chất hai số đối nhau:

(a – b)³ = [(-1)(b – a)]³ = (-1)³(b – a)³ = -1³.(b – a)³ = – (b – a)³

b) (- a – b)² = (a + b)²

Biến đổi vế trái thành vế phải:

(- a – b)² = [(-a) + (-b)]²

= (-a)² +2.(-a).(-b) + (-b)²

= a² + 2ab + b² = (a + b)²

Sử dụng tính chất hai số đối nhau:

(-a – b)² = [(-1) . (a + b)]² = (-1)² . (a + b)² = 1 . (a + b)² = (a + b)²

Bài tiếp theo: Giải Toán 8 bài 6: Phân tích đa thức thành nhân tử bằng phương pháp đặt nhân tử chung

Xem thêm:

Trên đây, VnDoc đã gửi tới các bạn tài liệu Giải Toán 8 bài 5: Những hằng đẳng thức đáng nhớ (tiếp). Để tham khảo lời giải những bài tiếp theo, mời các bạn vào chuyên mục Giải bài tập Toán lớp 8 trên VnDoc nhé. Chuyên mục tổng hợp lời giải Toán lớp 8 theo từng đơn vị bài học giúp các em nắm vững kiến thức được học trong từng bài, từ đó học tốt Toán 8 hơn.

Ngoài Soạn Toán 8, mời các bạn tham khảo thêm Giải SBT Toán 8, Giải Vở BT Toán 8 và các đề thi học học kì 1 lớp 8, đề thi học học kì 2 lớp 8 các môn Toán, Văn, Anh, Hóa... được cập nhật liên tục trên VnDoc.