Giải SBT Toán 11 Kết nối tri thức bài 1

Giá trị lượng giác của góc lượng giác

Giải sách bài tập Toán 11 Kết nối tri thức bài 1: Giá trị lượng giác của góc lượng giác

Bài 1.1 trang 7 SBT Toán 11 Kết nối
Bài 1.2 trang 7 SBT Toán 11 Kết nối
Bài 1.3 trang 7 SBT Toán 11 Kết nối
Bài 1.4 trang 7 SBT Toán 11 Kết nối
Bài 1.5 trang 7 SBT Toán 11 Kết nối
Bài 1.6 trang 7 SBT Toán 11 Kết nối
Bài 1.7 trang 8 SBT Toán 11 Kết nối
Bài 1.8 trang 8 SBT Toán 11 Kết nối
Bài 1.9 trang 8 SBT Toán 11 Kết nối

Giải sách bài tập Toán 11 Kết nối tri thức bài 1: Giá trị lượng giác của góc lượng giác được VnDoc.com sưu tầm và xin gửi tới bạn đọc cùng tham khảo để có thêm tài liệu học Toán 11 Kết nối tri thức nhé. Mời các bạn cùng theo dõi bài viết.

Bài 1.1 trang 7 SBT Toán 11 Kết nối

Số đo độ	20^o	?	150^o	500^o	?	?
Số đo radian	?	$\frac{11\pi }{2}$ $\frac{11\pi }{2}$	?	?	$\frac{-5\pi }{6}$ $\frac{-5\pi }{6}$	$\frac{7\pi }{15}$ $\frac{7\pi }{15}$

Bài làm

Số đo độ	20^o	990^o	150^o	500^o	-150^o	84^o
Số đo radian	$\frac{\pi }{9}$ $\frac{\pi }{9}$	$\frac{11\pi }{2}$ $\frac{11\pi }{2}$	$\frac{5\pi }{6}$ $\frac{5\pi }{6}$	$\frac{25\pi }{9}$ $\frac{25\pi }{9}$	$\frac{-5\pi }{6}$ $\frac{-5\pi }{6}$	$\frac{7\pi }{15}$ $\frac{7\pi }{15}$

Bài 1.2 trang 7 SBT Toán 11 Kết nối

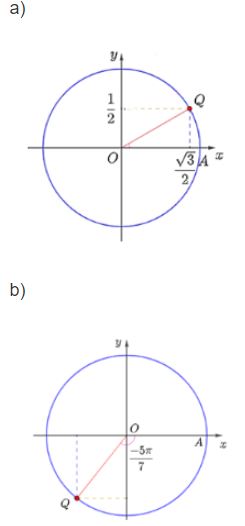
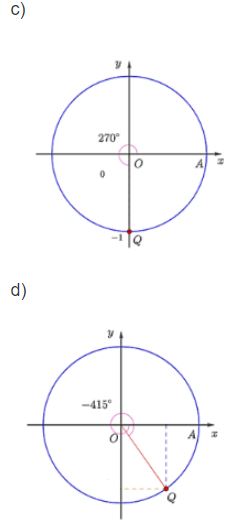
Trên đường tròn lượng giác, xác định điểm Q biểu diễn các góc lượng giác có số đo sau:

a) $\frac{\pi }{6}$ $\frac{\pi }{6}$

b) $\frac{-5\pi }{7}$ $\frac{-5\pi }{7}$

c) 270^o

d) −415^o

Bài làm

Giải sách bài tập Toán 11 Kết nối tri thức bài 1

Bài 1.3 trang 7 SBT Toán 11 Kết nối

Một đường tròn có bán kính 20 m. Tìm độ dài của cung trên đường tròn đó có số đo là:

a) $\frac{2\pi }{7}$ $\frac{2\pi }{7}$

b) 36^o

Bài làm

a) l = 20 . $\frac{2\pi }{7}$ $\frac{2\pi }{7}$ = $\frac{40\pi }{7}$ $\frac{40\pi }{7}$ (m)

b) l = 20 . $\frac{\pi.36 }{180}$ $\frac{\pi.36 }{180}$ = 4π (m)

Bài 1.4 trang 7 SBT Toán 11 Kết nối

Cho cosx = $-\frac{5}{13}$ $-\frac{5}{13}$ (90^o < x < 180^o). Tính các giá trị lượng giác còn lại của góc x

Bài làm

Ta có: $sin^{2}x+cox^{2}x=1$ $sin^{2}x+cox^{2}x=1$

Nên $sin^{2}x=1-cos^{2}x=1-(-\frac{5}{13})^{2}=\frac{144}{169}$ $sin^{2}x=1-cos^{2}x=1-(-\frac{5}{13})^{2}=\frac{144}{169}$

Mà $90^{o}< x <180^{o}$ $90^{o}< x <180^{o}$ nên sinx > 0

Do đó, $sinx=\sqrt{\frac{144}{169}}=\frac{12}{13}$ $sinx=\sqrt{\frac{144}{169}}=\frac{12}{13}$

Suy ra, $tanx=\frac{sinx}{cosx}=\frac{\frac{12}{13}}{-\frac{5}{13}}=\frac{-12}{5}$ $tanx=\frac{sinx}{cosx}=\frac{\frac{12}{13}}{-\frac{5}{13}}=\frac{-12}{5}$

$cotx = \frac{1}{tanx}=\frac{-5}{12}$ $cotx = \frac{1}{tanx}=\frac{-5}{12}$

Bài 1.5 trang 7 SBT Toán 11 Kết nối

Cho sin a + cos a = m. Hãy tính theo m.

a) sin a cos a;

b) sin³a + cos³a

c) sin⁴a + cos⁴a

Bài làm

a) sina + cosa = m nên $(sina+cosa)^{2}=m^{2}$ $(sina+cosa)^{2}=m^{2}$

$sin^{2}a+cos^{2}a+2sinacosa = m^{2}$ $sin^{2}a+cos^{2}a+2sinacosa = m^{2}$ hay $1+2 sinacosa=m^{2}$ $1+2 sinacosa=m^{2}$

Suy ra $sinacosa=\frac{m^{2}-1}{2}$ $sinacosa=\frac{m^{2}-1}{2}$

b) $sin^{3}a+cos^{3}a=(sina+cosa)^{3}-3sinacosa(sina+cosa)$ $sin^{3}a+cos^{3}a=(sina+cosa)^{3}-3sinacosa(sina+cosa)$

$= m^{3}-3m.\frac{m^{2}-1}{2}=\frac{3m-m^{3}}{2}$ $= m^{3}-3m.\frac{m^{2}-1}{2}=\frac{3m-m^{3}}{2}$

c) $sin^{4}a+cos^{4}a=(sin^{2}a+cos^{2}a)^{2}-2sin^{2}acos^{2}$ $sin^{4}a+cos^{4}a=(sin^{2}a+cos^{2}a)^{2}-2sin^{2}acos^{2}$

$=1-2(sinacosa)^{2}=1-2.(\frac{m^{2}-1}{2})^{2}$ $=1-2(sinacosa)^{2}=1-2.(\frac{m^{2}-1}{2})^{2}$

$=1-\frac{(m^{2}-1)^{2}}{2}$ $=1-\frac{(m^{2}-1)^{2}}{2}$

Bài 1.6 trang 7 SBT Toán 11 Kết nối

a) cos⁴x − sin⁴x = 2cos²x − 1

b) tan²x − sin²x = tan²x . sin²x

c) (sinx + cosx)² + (sinx − cosx)² = 2

Bài làm

a) $cos^{4}x -sin^{4}x$ $cos^{4}x -sin^{4}x$

$= (cos^{2} x- sin^{2}x)(cos^{2}x + sin^{2}x)$ $= (cos^{2} x- sin^{2}x)(cos^{2}x + sin^{2}x)$

$= cos^{2}x -sin^{2}x$ $= cos^{2}x -sin^{2}x$

$= cos^{2}x -(1 -cos^{2}x) = 2 cos^{2}x - 1$ $= cos^{2}x -(1 -cos^{2}x) = 2 cos^{2}x - 1$

b) $tan^{2}x-sin^{2}x$ $tan^{2}x-sin^{2}x$

$=\frac{sin^{2}x}{cos^{2}x}-sin^{2}x$ $=\frac{sin^{2}x}{cos^{2}x}-sin^{2}x$

$=\frac{sin^{2}x-sin^{2}xcos^{2}x}{cos^{2}x}$ $=\frac{sin^{2}x-sin^{2}xcos^{2}x}{cos^{2}x}$

$=\frac{sin^{2}x(1-cos^{2}x)}{cos^{2}x}$ $=\frac{sin^{2}x(1-cos^{2}x)}{cos^{2}x}$

$=\frac{sin^{2}x}{cos^{2}x}.sin^{2}x$ $=\frac{sin^{2}x}{cos^{2}x}.sin^{2}x$

$=tan^{2}xsin^{2}x$ $=tan^{2}xsin^{2}x$

c) $(sinx+cosx)^{2}+(sinx-cosx)^{2}$ $(sinx+cosx)^{2}+(sinx-cosx)^{2}$

$=sin^{2}x+2sinxcosx+cos^{2}x+sin^{2}x-2sinxcosx+cos^{2}x$ $=sin^{2}x+2sinxcosx+cos^{2}x+sin^{2}x-2sinxcosx+cos^{2}x$

$=2sin^{2}x+2cos^{2}x$ $=2sin^{2}x+2cos^{2}x$

$=2.(sin^{2}x+cos^{2}x)$ $=2.(sin^{2}x+cos^{2}x)$

= 2.1 =2

Bài 1.7 trang 8 SBT Toán 11 Kết nối

A = 2cos⁴x − sin⁴x + sin²xcos²x + 3sin²x.

Bài làm

A = $2cos^{4} x -sin^{4}x + sin^{2}x cos^{2}x + 3 sin^{2}x$ $2cos^{4} x -sin^{4}x + sin^{2}x cos^{2}x + 3 sin^{2}x$

$= cos^{4} x -sin^{4} x + cos^{4} x + sin^{2} x cos^{2} x + 3 sin^{2} x$ $= cos^{4} x -sin^{4} x + cos^{4} x + sin^{2} x cos^{2} x + 3 sin^{2} x$

$= (cos^{2} x -sin^{2} x)(cos^{2} x + sin^{2}x) + cos^{2}x (cos^{2}x + sin^{2}x) + 3sin^{2} x$ $= (cos^{2} x -sin^{2} x)(cos^{2} x + sin^{2}x) + cos^{2}x (cos^{2}x + sin^{2}x) + 3sin^{2} x$

$= cos^{2} x- sin^{2}x + cos^{2}x + 3 sin^{2}x$ $= cos^{2} x- sin^{2}x + cos^{2}x + 3 sin^{2}x$

$= 2cos^{2} x + 2 sin^{2} x$ $= 2cos^{2} x + 2 sin^{2} x$

$= 2(cos^{2}x + sin^{2} x)$ $= 2(cos^{2}x + sin^{2} x)$

= 2 . 1 = 2

Bài 1.8 trang 8 SBT Toán 11 Kết nối

Bánh xe của người đi xe đạp quay được 12 vòng trong 6 giây.

a) Tính góc (theo độ và rađian) mà bánh xe quay được trong 1 giây.

b) Tính quãng đường mà người đi xe đạp đã đi được trong 1 phút, biết rằng đường kính bánh xe đạp là 860 mm.

Bài làm

a) Trong 1 giây, bánh xe quay được 12/6 = 2 vòng, tức là quay được một góc 4π (rad) hay 720^o

b) Bán kính xe đạp là: 860 : 2 = 430 (mm).

Trong 1 phút, quãng đường mà người đi xe đã đi được là:

l = 430 . 4π . 60 = 103200π (mm).

Bài 1.9 trang 8 SBT Toán 11 Kết nối

Kim giờ dài 6 cm và kim phút dài 11 cm của đồng hồ chỉ 4 giờ. Hỏi thời gian ít nhất để 2 kim vuông góc với nhau là bao nhiêu? Lúc đó tổng quãng đường hai đầu mút kim giờ và kim phút đi được là bao nhiêu?

Bài làm

Một giờ, kim phút quét được một góc lượng giác $2\pi$ $2\pi$; kim giờ quét được một góc $\frac{\pi}{6}$ $\frac{\pi}{6}$

Hiệu vận tốc giữa kim phút và kim giờ là $2\pi-\frac{\pi}{6}=\frac{11\pi}{6}$ $2\pi-\frac{\pi}{6}=\frac{11\pi}{6}$

Vào lúc 4 giờ hai kim tạo với nhau một góc là $\frac{2\pi}{3}$ $\frac{2\pi}{3}$.

Khoảng thời gian ít nhất để hai kim vuông góc với nhau là

$(\frac{2\pi}{3}-\frac{\pi}{2}):\frac{11\pi}{6}=\frac{1}{11}$ $(\frac{2\pi}{3}-\frac{\pi}{2}):\frac{11\pi}{6}=\frac{1}{11}$ (giờ).

Vậy sau $\frac{1}{11}$ $\frac{1}{11}$ (giờ) hai kim sẽ vuông góc với nhau.

Tổng quãng đường hai đầu mút kim đi được là

$l=6.\frac{1}{11}.\frac{\pi}{6}+11.\frac{1}{11}.2\pi=\frac{23\pi}{11} (cm).$ $l=6.\frac{1}{11}.\frac{\pi}{6}+11.\frac{1}{11}.2\pi=\frac{23\pi}{11} (cm).$

Trắc nghiệm Toán 11 Kết nối tri thức bài 1

Bài trắc nghiệm số: 4186

----------------------------------------

Bài tiếp theo: Giải sách bài tập Toán 11 Kết nối tri thức bài 2

VnDoc.com vừa gửi tới bạn đọc bài viết Giải sách bài tập Toán 11 Kết nối tri thức bài 1: Giá trị lượng giác của góc lượng giác. Mời các bạn cùng tham khảo thêm tại mục Toán 11 Kết nối tri thức, Giải sách bài tập Toán 11 Kết nối tri thức.

Chia sẻ, đánh giá bài viết

1

108

Bài trước

Bài sau