Giao diện mới của VnDoc Pro: Dễ sử dụng hơn - chỉ tập trung vào lớp bạn quan tâm. Vui lòng chọn lớp mà bạn quan tâm: Lưu và trải nghiệm

VnDoc.com

Giải SBT Toán 11 Kết nối tri thức bài 4

Phương trình lượng giác cơ bản

Bài trước

Bài sau

Giải sách bài tậpT oán 11 Kết nối tri thức bài 4: Phương trình lượng giác cơ bản

Bài 1.25 trang 24 SBT Toán 11 Kết nối
Bài 1.26 trang 24 SBT Toán 11 Kết nối
Bài 1.27 trang 24 SBT Toán 11 Kết nối
Bài 1.28 trang 24 SBT Toán 11 Kết nối
Bài 1.29 trang 24 SBT Toán 11 Kết nối
Bài 1.30 trang 25 SBT Toán 11 Kết nối

VnDoc.com xin gửi tới bạn đọc bài viết Giải sách bài tập Toán 11 Kết nối tri thức bài 4: Phương trình lượng giác cơ bản để bạn đọc cùng tham khảo và có thêm tài liệu học Toán 11 Kết nối tri thức nhé. Mời các bạn cùng theo dõi bài viết dưới đây.

Bài 1.25 trang 24 SBT Toán 11 Kết nối

Giải các phương trình sau:

a) $2sin(\frac{x}{3}+15^{o})+\sqrt{2}=0$ $2sin(\frac{x}{3}+15^{o})+\sqrt{2}=0$

b) $cos(2x+\frac{\pi}{5})=-1$ $cos(2x+\frac{\pi}{5})=-1$

c) $3tan2x +\sqrt{3}=0$ $3tan2x +\sqrt{3}=0$

d) $cot(2x-3)=cot15^{o}$ $cot(2x-3)=cot15^{o}$

Bài làm

a) $2sin(\frac{x}{3}+15^{o})+\sqrt{2}=0$ $2sin(\frac{x}{3}+15^{o})+\sqrt{2}=0$

$\Leftrightarrow sin (\frac{x}{3}+15^{o})=-\frac{\sqrt{2}}{2}$ $\Leftrightarrow sin (\frac{x}{3}+15^{o})=-\frac{\sqrt{2}}{2}$

$\Leftrightarrow sin(\frac{x}{3} + 15^{o})=sin(-45^{o})$ $\Leftrightarrow sin(\frac{x}{3} + 15^{o})=sin(-45^{o})$

$\Leftrightarrow \frac{x}{3}+15^{o}=-45^{o}+k.360^{o}$ $\Leftrightarrow \frac{x}{3}+15^{o}=-45^{o}+k.360^{o}$ hoặc $\frac{x}{3}+15^{o}=180^{o}-(-45^{o})+k360^{o} (k\in \mathbb{Z})$ $\frac{x}{3}+15^{o}=180^{o}-(-45^{o})+k360^{o} (k\in \mathbb{Z})$

$\Leftrightarrow x=-180^{o} + k.1080^{o}$ $\Leftrightarrow x=-180^{o} + k.1080^{o}$ hoặc $x = 630^{o}+k.1080^{o} (k\in \mathbb{Z})$ $x = 630^{o}+k.1080^{o} (k\in \mathbb{Z})$

b) $cos(2x+\frac{\pi}{5})=-1$ $cos(2x+\frac{\pi}{5})=-1$

$\Leftrightarrow 2x +\frac{\pi}{5}=\pi + k2\pi (k \in \mathbb{Z})$ $\Leftrightarrow 2x +\frac{\pi}{5}=\pi + k2\pi (k \in \mathbb{Z})$

$\Leftrightarrow x =\frac{2\pi}{5}+ k \pi (k \in \mathbb{Z})$ $\Leftrightarrow x =\frac{2\pi}{5}+ k \pi (k \in \mathbb{Z})$

c) $3tan2x +\sqrt{3}=0$ $3tan2x +\sqrt{3}=0$

$\Leftrightarrow tan2x=-\frac{\sqrt{3}}{3}$ $\Leftrightarrow tan2x=-\frac{\sqrt{3}}{3}$

$\Leftrightarrow tan2x=tan(-\frac{\pi}{6})$ $\Leftrightarrow tan2x=tan(-\frac{\pi}{6})$

$\Leftrightarrow 2x =-\frac{\pi}{6}+k\pi (k \in \mathbb{Z})$ $\Leftrightarrow 2x =-\frac{\pi}{6}+k\pi (k \in \mathbb{Z})$

$\Leftrightarrow x = -\frac{\pi}{12}+k\frac{\pi}{2} (k \in \mathbb{Z})$ $\Leftrightarrow x = -\frac{\pi}{12}+k\frac{\pi}{2} (k \in \mathbb{Z})$

d) $cot(2x-3)=cot15^{o}$ $cot(2x-3)=cot15^{o}$

$\Leftrightarrow 2x-3 = 15^{o} + k.180^{o} (k \in \mathbb{Z})$ $\Leftrightarrow 2x-3 = 15^{o} + k.180^{o} (k \in \mathbb{Z})$

$\Leftrightarrow x = 1,5 + 7,5^{o} + k.90^{o} (k \in \mathbb{Z})$ $\Leftrightarrow x = 1,5 + 7,5^{o} + k.90^{o} (k \in \mathbb{Z})$

Bài 1.26 trang 24 SBT Toán 11 Kết nối

Giải các phương trình sau:

a) $sin(2x + 15^{o})+cos(2x-15^{o})-0$ $sin(2x + 15^{o})+cos(2x-15^{o})-0$

b) $cos(2x+\frac{\pi}{5})+cos(3x-\frac{\pi}{6})=0$ $cos(2x+\frac{\pi}{5})+cos(3x-\frac{\pi}{6})=0$

c) tanx + cotx = 0

d) sinx + tanx = 0

Bài làm

a) $sin(2x + 15^{o})+cos(2x-15^{o})-0$ $sin(2x + 15^{o})+cos(2x-15^{o})-0$

$\Leftrightarrow sin(2x + 15^{o})=-cos(2x-15^{o})$ $\Leftrightarrow sin(2x + 15^{o})=-cos(2x-15^{o})$

$\Leftrightarrow sin(2x+15^{o})=-sin[90^{o}-(2x-15^{o})]$ $\Leftrightarrow sin(2x+15^{o})=-sin[90^{o}-(2x-15^{o})]$

$\Leftrightarrow sin(2x + 15^{o})=sin[-90^{o}+(2x-15^{o})]$ $\Leftrightarrow sin(2x + 15^{o})=sin[-90^{o}+(2x-15^{o})]$

$\Leftrightarrow sin(2x + 15^{o}) = sin(2x-105^{o})$ $\Leftrightarrow sin(2x + 15^{o}) = sin(2x-105^{o})$

$\Leftrightarrow 2x + 15^{o}=2x-105^{o} +k.360^{o}$ $\Leftrightarrow 2x + 15^{o}=2x-105^{o} +k.360^{o}$ hoặc $2x+15^{o}=180^{o}-(2x-105^{o}) +k.360^{o} (k\in \mathbb{Z})$ $2x+15^{o}=180^{o}-(2x-105^{o}) +k.360^{o} (k\in \mathbb{Z})$

$\Leftrightarrow 120^{o} = k.360^{o}$ $\Leftrightarrow 120^{o} = k.360^{o}$ (không xảy ra) hoặc $x = 67,5^{o} + k.90^{o} (k \in \mathbb{Z})$ $x = 67,5^{o} + k.90^{o} (k \in \mathbb{Z})$

b) $cos(2x+\frac{\pi}{5})+cos(3x-\frac{\pi}{6})=0$ $cos(2x+\frac{\pi}{5})+cos(3x-\frac{\pi}{6})=0$

$\Leftrightarrow cos(2x+\frac{\pi}{5}=cos[\pi – (3x-\frac{\pi}{6})]$ $\Leftrightarrow cos(2x+\frac{\pi}{5}=cos[\pi – (3x-\frac{\pi}{6})]$

$\Leftrightarrow cos(2x+\frac{\pi}{5}=cos(\frac{7\pi}{6}-3x)$ $\Leftrightarrow cos(2x+\frac{\pi}{5}=cos(\frac{7\pi}{6}-3x)$

$\Leftrightarrow 2x+\frac{\pi}{5}=\frac{7\pi}{6}-3x+k2\pi$ $\Leftrightarrow 2x+\frac{\pi}{5}=\frac{7\pi}{6}-3x+k2\pi$ hoặc $2x+\frac{\pi}{5}=-(\frac{7\pi}{6}-2x)+k2\pi (k \in \mathbb{Z})$ $2x+\frac{\pi}{5}=-(\frac{7\pi}{6}-2x)+k2\pi (k \in \mathbb{Z})$

$\Leftrightarrow x = \frac{29\pi}{150} + k\frac{2\pi}{5}$ $\Leftrightarrow x = \frac{29\pi}{150} + k\frac{2\pi}{5}$ hoặc $x = \frac{41\pi}{30}-k2\pi (k \in \mathbb{Z})$ $x = \frac{41\pi}{30}-k2\pi (k \in \mathbb{Z})$

c) tanx + cotx = 0

$\Leftrightarrow tanx = -cotx$ $\Leftrightarrow tanx = -cotx$

$\Leftrightarrow tan x = cot (\pi – x)$ $\Leftrightarrow tan x = cot (\pi – x)$

$\Leftrightarrow tan x = tan[\frac{\pi}{2}-(\pi-x)]$ $\Leftrightarrow tan x = tan[\frac{\pi}{2}-(\pi-x)]$

$\Leftrightarrow tanx = tan(x - \frac{\pi}{2})$ $\Leftrightarrow tanx = tan(x - \frac{\pi}{2})$

$\Leftrightarrow x = x-\frac{\pi}{2}+k\pi (k \in \mathbb{Z})$ $\Leftrightarrow x = x-\frac{\pi}{2}+k\pi (k \in \mathbb{Z})$

$\Leftrightarrow \frac{\pi}{2}- k \pi = 0 (k \in \mathbb{Z})$ $\Leftrightarrow \frac{\pi}{2}- k \pi = 0 (k \in \mathbb{Z})$ (vô lý)

Vậy phương trình vô nghiệm

d) sinx + tanx = 0 (Điều kiện $cos x \neq 0$ $cos x \neq 0$ )

$\Leftrightarrow sinx + \frac{sinx}{cosx}=0$ $\Leftrightarrow sinx + \frac{sinx}{cosx}=0$

$\Leftrightarrow sinx(1+\frac{1}{cosx}) = 0$ $\Leftrightarrow sinx(1+\frac{1}{cosx}) = 0$

$\Leftrightarrow sinx = 0$ $\Leftrightarrow sinx = 0$ hoặc $1+\frac{1}{cosx}=0$ $1+\frac{1}{cosx}=0$

$\Leftrightarrow sinx = 0$ $\Leftrightarrow sinx = 0$ hoặc cosx = -1

$\Leftrightarrow sinx = 0 (do sin^{2}x+cos^{2}x=1 )$ $\Leftrightarrow sinx = 0 (do sin^{2}x+cos^{2}x=1 )$

$\Leftrightarrow x = k\pi (k \in \mathbb{Z})$ $\Leftrightarrow x = k\pi (k \in \mathbb{Z})$

Bài 1.27 trang 24 SBT Toán 11 Kết nối

Giải các phương trình sau:

a) (2 + cosx)(3cos2x–1) = 0;

b) 2sin2x – sin4x = 0;

c) cos⁶x - sin⁶x = 0 ;

d) tan2x.cotx = 1.

Bài làm

a) Ta có (2 + cosx)(3cos2x – 1) = 0

$\Leftrightarrow$ $\Leftrightarrow$ 2 + cosx= 0 hoặc 3cos2x – 1=0

+ Phương trình 2 + cosx = 0 vô nghiệm vì $-1 \leq cos x \leq 1$ $-1 \leq cos x \leq 1$.

+ Gọi $\alpha$ $\alpha$ là góc thoả mãn $cos\alpha =\frac{1}{3}$ $cos\alpha =\frac{1}{3}$. Ta có

$3cos2x -1=0\Leftrightarrow cos2x = cos\alpha \Leftrightarrow2x = \pm \alpha +k2\pi$ $3cos2x -1=0\Leftrightarrow cos2x = cos\alpha \Leftrightarrow2x = \pm \alpha +k2\pi$

$\Leftrightarrow x = \pm \frac{\alpha}{2} + k\pi (k\in \mathbb{Z})$ $\Leftrightarrow x = \pm \frac{\alpha}{2} + k\pi (k\in \mathbb{Z})$

Vậy nghiệm của phương trình đã cho là $x = \pm \frac{\alpha}{2} + k\pi (k \in \mathbb{Z})$ $x = \pm \frac{\alpha}{2} + k\pi (k \in \mathbb{Z})$ với $cos\alpha = \frac{1}{3}$ $cos\alpha = \frac{1}{3}$

b) Ta có 2sin2x - sin4x = 0

$\Leftrightarrow$ $\Leftrightarrow$ 2sin2x - 2sin2xcos2x = 0

$\Leftrightarrow$ $\Leftrightarrow$ 2sin2x(1 - cos2x) = 0

$\Leftrightarrow$ $\Leftrightarrow$ sin2x = 0 hoặc cos2x =1

Do $sin^{2}2x+cos^{2}2x=1$ $sin^{2}2x+cos^{2}2x=1$ nên cos2x = 1 kéo theo sin2x = 0, do đó phương trình đã cho tương đương với

$sin2x= 0 \Leftrightarrow 2x = k\pi \Leftrightarrow x = k\frac{\pi}{2} ( k \in \mathbb{Z})$ $sin2x= 0 \Leftrightarrow 2x = k\pi \Leftrightarrow x = k\frac{\pi}{2} ( k \in \mathbb{Z})$

c) Ta có $cos^{6}x -sin^{6}x=0$ $cos^{6}x -sin^{6}x=0$

$\Leftrightarrow cos^{6}x =sin^{6}x$ $\Leftrightarrow cos^{6}x =sin^{6}x$

$\Leftrightarrow (cos^{2}x)^{3} = (sin^{2}x)^{3}$ $\Leftrightarrow (cos^{2}x)^{3} = (sin^{2}x)^{3}$

$\Leftrightarrow cos^{2}x = sin^{2}x$ $\Leftrightarrow cos^{2}x = sin^{2}x$

$\Leftrightarrow cos^{2}x -sin^{2}x=0$ $\Leftrightarrow cos^{2}x -sin^{2}x=0$

$\Leftrightarrow cos2x=0$ $\Leftrightarrow cos2x=0$

$\Leftrightarrow 2x =\frac{\pi}{2} + k\pi (k \in \mathbb{Z})$ $\Leftrightarrow 2x =\frac{\pi}{2} + k\pi (k \in \mathbb{Z})$

$\Leftrightarrow x = \frac{\pi}{4} + k\frac{\pi}{2} (k \in \mathbb{Z})$ $\Leftrightarrow x = \frac{\pi}{4} + k\frac{\pi}{2} (k \in \mathbb{Z})$

d) Điều kiện $sinx \neq 0$ $sinx \neq 0$ và $cos2x \neq 0$ $cos2x \neq 0$

Ta có tan 2xcotx = 1

$\Leftrightarrow tan2x = \frac{1}{cotx}$ $\Leftrightarrow tan2x = \frac{1}{cotx}$

$\Leftrightarrow tan2x = tanx$ $\Leftrightarrow tan2x = tanx$

$\Leftrightarrow 2x = x +k\pi (k \in \mathbb{Z})$ $\Leftrightarrow 2x = x +k\pi (k \in \mathbb{Z})$

$\Leftrightarrow x = k\pi ( k \in \mathbb{Z})$ $\Leftrightarrow x = k\pi ( k \in \mathbb{Z})$

Ta thấy $x = k\pi ( k \in \mathbb{Z})$ $x = k\pi ( k \in \mathbb{Z})$ không thoả mãn điều kiện $sinx \neq 0$ $sinx \neq 0$

Vậy phương trình đã cho vô nghiệm

Bài 1.28 trang 24 SBT Toán 11 Kết nối

Tìm các giá trị của x để giá trị tương ứng của các hàm số sau bằng nhau:

a) $y=cos(2x-\frac{\pi}{3})$ $y=cos(2x-\frac{\pi}{3})$ và $y=cos(x-\frac{\pi}{4})$ $y=cos(x-\frac{\pi}{4})$

b) $y=sin(3x-\frac{\pi}{4})$ $y=sin(3x-\frac{\pi}{4})$ và $y= sin(x-\frac{\pi}{6})$ $y= sin(x-\frac{\pi}{6})$

Bài làm

a) Ta có: $cos(2x-\frac{\pi}{3}) = cos(x-\frac{\pi}{4})$ $cos(2x-\frac{\pi}{3}) = cos(x-\frac{\pi}{4})$

$\Leftrightarrow 2x -\frac{\pi}{3} = x-\frac{\pi}{4} +k2\pi$ $\Leftrightarrow 2x -\frac{\pi}{3} = x-\frac{\pi}{4} +k2\pi$ hoặc $2x-\frac{\pi}{3}=-(x-\frac{\pi}{4})+k2\pi (k \in \mathbb{Z})$ $2x-\frac{\pi}{3}=-(x-\frac{\pi}{4})+k2\pi (k \in \mathbb{Z})$

$\Leftrightarrow x =\frac{\pi}{12} +k2\pi$ $\Leftrightarrow x =\frac{\pi}{12} +k2\pi$ hoặc $x = \frac{7\pi}{36} +k\frac{2\pi}{3} (k \in \mathbb{Z})$ $x = \frac{7\pi}{36} +k\frac{2\pi}{3} (k \in \mathbb{Z})$

b) Ta có: $sin(3x-\frac{\pi}{4}=sin(x-\frac{\pi}{6})$ $sin(3x-\frac{\pi}{4}=sin(x-\frac{\pi}{6})$

$\Leftrightarrow 3x-\frac{\pi}{4}=x-\frac{\pi}{6} + k2\pi$ $\Leftrightarrow 3x-\frac{\pi}{4}=x-\frac{\pi}{6} + k2\pi$ hoặc $3x-\frac{\pi}{4}=\pi-(x-\frac{\pi}{6})+k2\pi$ $3x-\frac{\pi}{4}=\pi-(x-\frac{\pi}{6})+k2\pi$ ( $k \in \mathbb{Z}$ $k \in \mathbb{Z}$)

$\Leftrightarrow x =\frac{\pi}{24} +k2\pi$ $\Leftrightarrow x =\frac{\pi}{24} +k2\pi$ hoặc $x=\frac{17\pi}{48} +k\frac{\pi}{2} (k \in \mathbb{Z})$ $x=\frac{17\pi}{48} +k\frac{\pi}{2} (k \in \mathbb{Z})$

Bài 1.29 trang 24 SBT Toán 11 Kết nối

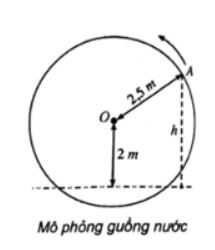
Một chiếc guồng nước có dạng hình tròn bán kính 2,5 m; trục của nó đặt cách mặt nước 2 m (hình bên). Khi guồng quay đều, khoảng cách h (mét) tính từ một chiếc gầu gắn tại điểm A trên guồng đến mặt nước là h = |y| trong đó

$y=2+2,5sin2\pi (x-\frac{1}{4})$ $y=2+2,5sin2\pi (x-\frac{1}{4})$

với x là thời gian quay của guồng ( $x \geq 0$ $x \geq 0$), tính bằng phút; ta quy ước rằng y > 0 khi gầu ở trên mặt nước và y < 0 khi gầu ở dưới mặt nước.

a) Khi nào chiếc gầu ở vị trí cao nhất? Thấp nhất?

b) Chiếc gầu cách mặt nước 2 mét lần đầu tiên khi nào?

Giải sách bài tập Toán 11 Kết nối tri thức bài 4

Bài làm

a) Vì $-1 \leq sin2\pi (x-\frac{1}{4}) \leq 1$ $-1 \leq sin2\pi (x-\frac{1}{4}) \leq 1$ nên $-2,5 \leq 2,5 sin2\pi (x-\frac{1}{4}) \leq 2,5$ $-2,5 \leq 2,5 sin2\pi (x-\frac{1}{4}) \leq 2,5$ và do đó ta có $2-2,5 \leq 2+2,5sin2\pi (x-\frac{1}{4}) \leq 2+ 2,5$ $2-2,5 \leq 2+2,5sin2\pi (x-\frac{1}{4}) \leq 2+ 2,5$

Hay $-0,5 \leq 2 + 2,5 sin2\pi (x-\frac{1}{4}) \leq 4,5 \forall x \in \mathbb{R}$ $-0,5 \leq 2 + 2,5 sin2\pi (x-\frac{1}{4}) \leq 4,5 \forall x \in \mathbb{R}$

Suy ra, gầu ở vị trí cao nhất khi $sin 2\pi (x-\frac{1}{4})=1$ $sin 2\pi (x-\frac{1}{4})=1$

$\Leftrightarrow 2\pi(x-\frac{1}{4})=\frac{\pi}{2} +k2\pi (k \in \mathbb{Z})$ $\Leftrightarrow 2\pi(x-\frac{1}{4})=\frac{\pi}{2} +k2\pi (k \in \mathbb{Z})$

$\Leftrightarrow x=\frac{1}{2} +k (k \in \mathbb{Z})$ $\Leftrightarrow x=\frac{1}{2} +k (k \in \mathbb{Z})$ Do $x \geq 0$ $x \geq 0$ nên $x=\frac{1}{2}+k (k \in \mathbb{N})$ $x=\frac{1}{2}+k (k \in \mathbb{N})$

Vậy gầu ở vị trí cao nhất tại các thời điểm 12, 32, 52,...12, 32, 52,... phút.

Tương tự, gầu ở vị trí thấp nhất khi $sin2\pi(x-\frac{1}{4})=-1$ $sin2\pi(x-\frac{1}{4})=-1$

$\Leftrightarrow 2\pi(x-\frac{1}{4})=\frac{\pi}{2}+k2\pi (k \in \mathbb{Z})$ $\Leftrightarrow 2\pi(x-\frac{1}{4})=\frac{\pi}{2}+k2\pi (k \in \mathbb{Z})$

$x=\frac{1}{2} + k(k\in \mathbb{Z})$ $x=\frac{1}{2} + k(k\in \mathbb{Z})$. Do $x \geq 0$ $x \geq 0$ nên x =k ( $k \in \mathbb{N}$ $k \in \mathbb{N}$)

Vậy gàu ở vị trí thấp nhất tại các thời điểm 0, 1, 2, 3, ... phút.

b) Gầu cách mặt nước 2 m khi $2+2,5 sin2\pi (x-\frac{1}{4})=2$ $2+2,5 sin2\pi (x-\frac{1}{4})=2$

$\Leftrightarrow sin2\pi (x-\frac{1}{4})=0$ $\Leftrightarrow sin2\pi (x-\frac{1}{4})=0$

$\Leftrightarrow 2\pi (x-\frac{1}{4})=k\pi (k \in \mathbb{Z})$ $\Leftrightarrow 2\pi (x-\frac{1}{4})=k\pi (k \in \mathbb{Z})$

$\Leftrightarrow x = \frac{1}{4} +\frac{k}{2} (k \in \mathbb{Z})$ $\Leftrightarrow x = \frac{1}{4} +\frac{k}{2} (k \in \mathbb{Z})$

Do $x \geq 0$ $x \geq 0$ nên $x =\frac{1}{4}+\frac{k}{2} (k \in \mathbb{N})$ $x =\frac{1}{4}+\frac{k}{2} (k \in \mathbb{N})$

Vậy chiếc gầu cách mặt nước 2 m lần đầu tiên tại thời điểm $x=\frac{1}{4}$ $x=\frac{1}{4}$ phút.

Bài 1.30 trang 25 SBT Toán 11 Kết nối

Số giờ có ánh sáng mặt trời của một thành phố A trong ngày thứ t (ở đây t là số ngày tính từ ngày 1 tháng giêng) của một năm không nhuận được mô hình hóa bởi hàm số

$L(t) =12+2,83sin(\frac{2\pi}{365} (t-80))$ $L(t) =12+2,83sin(\frac{2\pi}{365} (t-80))$ với $t \in \mathbb{Z}$ $t \in \mathbb{Z}$ và $0 < t \leq 365$ $0 < t \leq 365$

a) Vào ngày nào trong năm thì thành phố A có ít giờ ánh sáng mặt trời nhất?

b) Vào ngày nào trong năm thì thành phố A có nhiều giờ ánh sáng mặt trời nhất?

c) Vào ngày nào trong năm thì thành phố A có khoảng 10 giờ ánh sáng mặt trời?

Bài làm

Vì $-1\leq sin(\frac{2\pi}{365}(t-80)) \leq 1$ $-1\leq sin(\frac{2\pi}{365}(t-80)) \leq 1$

Nên $-2,83 \leq 2,83sin(\frac{2\pi}{365}(t-80)) \leq 2,83$ $-2,83 \leq 2,83sin(\frac{2\pi}{365}(t-80)) \leq 2,83$

Suy ra $12-2,83 \leq 12 + 2,83sin(\frac{2\pi}{365}(t-80)) \leq 12 + 2,83$ $12-2,83 \leq 12 + 2,83sin(\frac{2\pi}{365}(t-80)) \leq 12 + 2,83$

hay $9,17 \leq 12 + 2,83sin(\frac{2\pi}{365}(t-80)) \leq 14,83 \forall t \in \mathbb{R}$ $9,17 \leq 12 + 2,83sin(\frac{2\pi}{365}(t-80)) \leq 14,83 \forall t \in \mathbb{R}$

a) Ngày thành phố A có ít giờ ánh sáng mặt trời nhất ứng với

$sin(\frac{2\pi}{365}(t-80))=-1$ $sin(\frac{2\pi}{365}(t-80))=-1$

$\Leftrightarrow \frac{2\pi}{365} (t-80) =-\frac{\pi}{2}+k2\pi (k \in \mathbb{Z})$ $\Leftrightarrow \frac{2\pi}{365} (t-80) =-\frac{\pi}{2}+k2\pi (k \in \mathbb{Z})$

$\Leftrightarrow t =-\frac{45}{4} + 365k ( k\in \mathbb{Z})$ $\Leftrightarrow t =-\frac{45}{4} + 365k ( k\in \mathbb{Z})$

Vì $0 < t \leq 365$ $0 < t \leq 365$ nên k = 1 suy ra $t=-\frac{45}{4}+365=353,75$ $t=-\frac{45}{4}+365=353,75$

Như vậy, vào ngày thứ 353 của năm, tức là khoảng ngày 20 tháng 12 thì thành phố A sẽ có ít giờ ánh sáng mặt trời nhất.

b) Ngày thành phố A có nhiều giờ ánh sáng mặt trời nhất ứng với

$sin(\frac{2\pi}{365}(t-80))=1$ $sin(\frac{2\pi}{365}(t-80))=1$

$\Leftrightarrow \frac{2\pi}{365} (t-80)=\frac{\pi}{2}+k2\pi ( k\in \mathbb{Z})$ $\Leftrightarrow \frac{2\pi}{365} (t-80)=\frac{\pi}{2}+k2\pi ( k\in \mathbb{Z})$

$\Leftrightarrow t =\frac{685}{4} + 365k ( k\in \mathbb{Z})$ $\Leftrightarrow t =\frac{685}{4} + 365k ( k\in \mathbb{Z})$

Vì $0 < t\leq 365$ $0 < t\leq 365$ nên k = 0 suy ra $t =\frac{685}{4}=171,25$ $t =\frac{685}{4}=171,25$

Như vậy, vào ngày thứ 171 của năm, tức là khoảng ngày 20 tháng 6 thì thành phố A sẽ có nhiều giờ ánh sáng mặt trời nhất.

c) Thành phố A có khoảng 10 giờ ánh sáng mặt trời trong ngày nếu

$12 + 2,83 sin(\frac{2\pi}{365}(t-80))=10$ $12 + 2,83 sin(\frac{2\pi}{365}(t-80))=10$

$\Leftrightarrow sin(\frac{2\pi}{365}(t-80))=\frac{-200}{283}$ $\Leftrightarrow sin(\frac{2\pi}{365}(t-80))=\frac{-200}{283}$

$\Leftrightarrow \frac{2\pi}{365}(t-80) \approx -0,78 +k2\pi$ $\Leftrightarrow \frac{2\pi}{365}(t-80) \approx -0,78 +k2\pi$ hoặc $\frac{2\pi}{365}(t-80) \approx 3,93 +k2\pi (k \in \mathbb{Z})$ $\frac{2\pi}{365}(t-80) \approx 3,93 +k2\pi (k \in \mathbb{Z})$

Từ đó ta được $t \approx 34,69 + 365 k$ $t \approx 34,69 + 365 k$ hoặc $t \approx 308,2 + 365k (k\in \mathbb{Z})$ $t \approx 308,2 + 365k (k\in \mathbb{Z})$

Vì $0 < t \leq 365$ $0 < t \leq 365$ nên k = 0 suy ra $t \approx 34,69$ $t \approx 34,69$ hoặc $t \approx 308,3$ $t \approx 308,3$

Như vậy, vào khoảng ngày thứ 34 của năm, tức là ngày 3 tháng 2 và ngày thứ 308 của năm, tức là ngày 4 tháng 11 thành phố A sẽ có 10 giờ ánh sáng mặt trời.

Luyện tập Toán 11 Kết nối tri thức bài 4

Bài trắc nghiệm số: 4206

-------------------------------------------

Bài tiếp theo: Giải sách bài tập Toán 11 Kết nối tri thức bài tập cuối chương 1

VnDoc.com vừa gửi tới bạn đọc bài viết Giải sách bài tập Toán 11 Kết nối tri thức bài 4: Phương trình lượng giác cơ bản. Mời các bạn cùng tham khảo thêm tại mục Toán 11 Kết nối tri thức, Giải sách bài tập Toán 11 Kết nối tri thức.

Chia sẻ, đánh giá bài viết

Bài trước

Bài sau