Cho hàm số y = ax2 có đồ thị là (P). Để (P) cắt đường thẳng (d): y = 2x + 3 tại điểm có tung độ là 1 thì giá trị của a = ......1
Cho hàm số y = ax2 có đồ thị là (P). Để (P) cắt đường thẳng (d): y = 2x + 3 tại điểm có tung độ là 1 thì giá trị của a = ......1
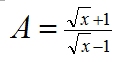
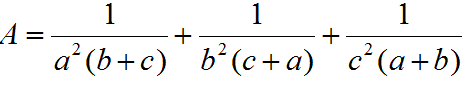 là: ............
là: ............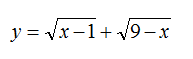 là: ............
là: ............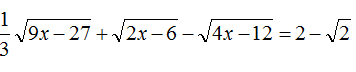 có nghiệm là: x = ..............
có nghiệm là: x = ..............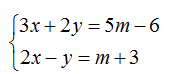
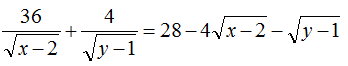
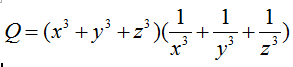 là:
là:


