When the polynomial f(x) = 3x3 + 2x2 + 5x + 1 is divided by g(x) = x + 1, the remainder is ............-5
When the polynomial f(x) = 3x3 + 2x2 + 5x + 1 is divided by g(x) = x + 1, the remainder is ............-5
Vòng 10 (vòng thi cấp quốc gia) của Cuộc thi giải Toán Tiếng Anh qua mạng năm 2015 - 2016 bắt đầu mở từ ngày 08/04/2016. Để ôn tập và chuẩn bị cho vòng thi này mời các bạn tham khảo bài test Đề thi Violympic Toán Tiếng Anh lớp 8 vòng 10 năm 2014 - 2015 trên trang VnDoc.com. Tham gia làm bài test để mở rộng vốn từ vựng tiếng anh về toán học đồng thời nâng cao kỹ năng giải toán nhé!
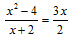 then x = .............-4
then x = .............-4
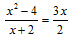 then x = .............-4
then x = .............-4
Given that 75k is perfect cube, the least positive integer k is ...........
45Given that 75k is perfect cube, the least positive integer k is ...........
45If n is a natural number such that n2 - 5 is a square number, then n = .......
3If n is a natural number such that n2 - 5 is a square number, then n = .......
3Given two numbers x, y such that (4y2 - 12y + 25)(4x2 + 6x + 4) = 28
The ratio of y to x is ..........
Given two numbers x, y such that (4y2 - 12y + 25)(4x2 + 6x + 4) = 28
The ratio of y to x is ..........
Exam number 2: Choose the best answer.
Question 1:Question 2:
Find the value of the constant m such that the polynomial f(x) = x3 - x + m is divisible by x + 2.Question 3:
If x = 3; y = -1 then x5 + 5x4y + 10x3y2 + 10x2y3 + 5xy4 + y5 = .................Question 4:
Which of the following statements is NOT true?
Question 5:
As shown in the figure, the length of BE is .............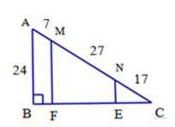
Question 6:
On a car trip Sam drove m miles, Kara drove twice as many miles as Sam did and Darin drove 20 miles less than Kara did. In terms of m, how many miles did Darin drive?
Question 7:
Given that two numbers x and y satisfy 2 < x < 3 and 7 < y < 8. Which of the following expressions has the greatest value?Question 8:
The solution set of the equation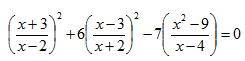 is S = {........}
is S = {........}
Question 9:
Let f(x) the polynomial given by f(x) = (1 + 2x + 3x2 + 4x3 + 5x4 + 84x5)
Suppose that f(x) = ao + a1x + a2x2 + ..... + ..... + a50x50.
The value of T = a1 + a2 + .... + a50 is .........
Question 10:
The maximum value ofGiven the function f(x) = 1/4 .m(m + 2)x2 + 3/2. mx + 3 with f(2) = -3.
The greatest possible value of m is .........
Given the function f(x) = 1/4 .m(m + 2)x2 + 3/2. mx + 3 with f(2) = -3.
The greatest possible value of m is .........
In the xy - plane, given three points A(-1; 2); B(-1; 8); C(5; 8). If ABCD is a square then the coordinate of D is (.....). Write your answer with the semicolon between x- coordinate and y- coordinate.
(5; 2)In the xy - plane, given three points A(-1; 2); B(-1; 8); C(5; 8). If ABCD is a square then the coordinate of D is (.....). Write your answer with the semicolon between x- coordinate and y- coordinate.
(5; 2)Find the area of the trapezoid ABCD, BC // AD, AB = CD = 5cm, BC = 10cm, AD = 16cm.
The area of the trapezoid ABCD is .........cm2.
Find the area of the trapezoid ABCD, BC // AD, AB = CD = 5cm, BC = 10cm, AD = 16cm.
The area of the trapezoid ABCD is .........cm2.
Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây: