If a + b = 3, a2 + b2 = 7 then a3 + b3 = ..........
Answer: ...............18
If a + b = 3, a2 + b2 = 7 then a3 + b3 = ..........
Answer: ...............18
Vòng thi quốc gia của Cuộc thi giải Toán Tiếng Anh qua mạng năm 2015 - 2016 đã bắt đầu mở từ ngày 08/04/2016. Mời các bạn học sinh lớp 8 tham gia làm bài test Đề thi Violympic Toán Tiếng Anh lớp 8 vòng 10 năm 2015 - 2016 trên trang VnDoc.com để thử sức với vòng thi này. Chúc các bạn làm bài tốt!
Mời các bạn tham khảo thêm:
Find the value of k such that x3 + kx2 + (4 - k)x - 35 is divisible by x - 7.
Answer: k = ........
Find the value of k such that x3 + kx2 + (4 - k)x - 35 is divisible by x - 7.
Answer: k = ........
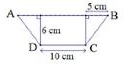
Figure is not drawn to scale.
Answer: The area of the trapezoid is ..........cm2.

Figure is not drawn to scale.
Answer: The area of the trapezoid is ..........cm2.
Find the value of x such that: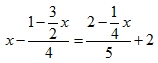
Answer: x = ...............
Find the value of x such that: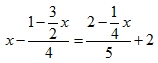
Answer: x = ...............
Let ABCD be a trapezoid with AB // CD, Â = D = 90o and AB = AD = CD/2.
Find the measure of the angle BCD.
Answer: BCD = ..........o.
Let ABCD be a trapezoid with AB // CD, Â = D = 90o and AB = AD = CD/2.
Find the measure of the angle BCD.
Answer: BCD = ..........o.
Let ABCD.A'B'C'D' be a cube with AC' = √3cm. Find the total surface area of this cube.
Answer: ..........cm2.
Let ABCD.A'B'C'D' be a cube with AC' = √3cm. Find the total surface area of this cube.
Answer: ..........cm2.
Bottle A contains 15% syrup. Bottle B contains 40% syrup. When these 2 bottles of syrup are mixed, the syrup content is 30% and the total volume is 600ml. How much syrup is in the bottle A at first?
Answer: ..........ml.
Bottle A contains 15% syrup. Bottle B contains 40% syrup. When these 2 bottles of syrup are mixed, the syrup content is 30% and the total volume is 600ml. How much syrup is in the bottle A at first?
Answer: ..........ml.
Let ABC be a triangle with AB = 3cm, AC = 7cm. The internal bisector of the angle BAC intersects BC at D. The line passing through D and parallel to AC cuts AB at E. Find the measure of DE.
Answer: DE = ..........cm.
Let ABC be a triangle with AB = 3cm, AC = 7cm. The internal bisector of the angle BAC intersects BC at D. The line passing through D and parallel to AC cuts AB at E. Find the measure of DE.
Answer: DE = ..........cm.
Given the equation (x - m)(m - 1) + (x - 1)(m + 1) = -2m.
Find all values of m such that this equation has no solution.
Answer: m = ...........
Given the equation (x - m)(m - 1) + (x - 1)(m + 1) = -2m.
Find all values of m such that this equation has no solution.
Answer: m = ...........
Given the equation: ![]()
The average (arithmetic mean) of all roots of this equation is ...........
Given the equation: ![]()
The average (arithmetic mean) of all roots of this equation is ...........
The Ford car left Hanoi for Nghe An and the Audi car left Nghe An for Ha Noi at the same time. The ratio of their speeds (the Ford car to the Audi car) was 4 : 3. The Ford decreased its speed by 25% and the Audi car increased its speed by 25% after they had passed each other.
When the Ford car reached Nghe An, the Audi car was still 20km away from Hanoi. The distance between Hanoi and Nghe An is ...... km.
The Ford car left Hanoi for Nghe An and the Audi car left Nghe An for Ha Noi at the same time. The ratio of their speeds (the Ford car to the Audi car) was 4 : 3. The Ford decreased its speed by 25% and the Audi car increased its speed by 25% after they had passed each other.
When the Ford car reached Nghe An, the Audi car was still 20km away from Hanoi. The distance between Hanoi and Nghe An is ...... km.
Suppose that the polynomial f(x) = x5 - x4 - 4x3 + 2x2 + 4x + 1 has 5 solutions x1; x2; x3; x4; x5. The other polynomial k(x) = x2 - 4.
Find the value of P = k(x1) x k(x2) x k(x3) x k(x4) x k(x5)
Answer: P = .............
Suppose that the polynomial f(x) = x5 - x4 - 4x3 + 2x2 + 4x + 1 has 5 solutions x1; x2; x3; x4; x5. The other polynomial k(x) = x2 - 4.
Find the value of P = k(x1) x k(x2) x k(x3) x k(x4) x k(x5)
Answer: P = .............
The smallest value of ![]() is .............
is .............
The smallest value of ![]() is .............
is .............
Exam number 2: Cóc vàng tài ba
Question 1: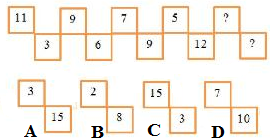
Question 2:
Assume that two numbers x and y satisfy: 2x + y = 6.
Find the minimum value of expression A = 4x2 + y2
Question 3:
ABCD is a square of side length 5cm. DEFG is a square of side length 3cm such that E lies on the extension of CD and G lies on AD. Find the area, in cm2, of triangle BDF.
Question 4:
In the xy - plane, given three points A(-1; 2); B(-3; -1); D(6; 2).
If ABCD is a parallelogram then C = ........
Question 5:
If a and b are two non-zero distinct numbers such that 3a2 + 4b2 = 7ab then the value of the expression is ...........
Question 6:
Given the rectangle whose perimeter is 24cm. If its length is decreased by 1cm and its width is increased by 1cm, then the area of the original rectanle is increased by 3cm2. Find the area of the original rectangle.
Question 7:
The triangle ABC has AB = 5cm, AC = 8cm, Â = 60o and the internal bisector AD (D ∈ BC). The length of BD is .........cm.
Question 8:
What number should replace the question mark?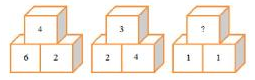
Question 9:
If all roots of the polynomial P(x) = x2 + 5x - 1 are also roots of the polynomial Q(x) = x3 + ax2 + bx + c then the value of a + b + 6c is ............Question 10:
Let ABC be an isoceles triangle (AB = AC) and its area is 501cm2. BD is the internal bisector of the angle ABC (D ∈ AC), E is a point on the opposite ray of CA such that CE = CB. I is a point on BC such that CI = 1/2 BI. The line EI meets AB at K, BD meets KC at H. Find the area of the triangle AHC.
Find the greatest interger number x such that the value of (3x - 2)/4 is greater than the value of (5x + 3)/5.
Answer: The greatest integer number x is .........
Find the greatest interger number x such that the value of (3x - 2)/4 is greater than the value of (5x + 3)/5.
Answer: The greatest integer number x is .........
How many sides does a polygon have if the number of its diagonals is as triple as the number of its sides?
Answer: The number of its sides is ............
How many sides does a polygon have if the number of its diagonals is as triple as the number of its sides?
Answer: The number of its sides is ............
Find the positive value of k such that x = 2 is a root of the following equation: x2 - kx + k2 - 4 = 0
Answer: k = ..........
Find the positive value of k such that x = 2 is a root of the following equation: x2 - kx + k2 - 4 = 0
Answer: k = ..........
If x, y, z satisfy these equations yz = 3/2 - x2/2; zx = 1/2 - y2/2 and xy = 5/2 - z2/2 then the value of Ιx + y + zΙ is ...........
3If x, y, z satisfy these equations yz = 3/2 - x2/2; zx = 1/2 - y2/2 and xy = 5/2 - z2/2 then the value of Ιx + y + zΙ is ...........
3Find the remainder when (x + 2)(x + 3)(x + 4)(x + 5) + 2017 is divided by x2 + 7x + 11.
Answer:
The remainder is .........
Find the remainder when (x + 2)(x + 3)(x + 4)(x + 5) + 2017 is divided by x2 + 7x + 11.
Answer:
The remainder is .........
A rectangle has a length of 60cm and a width of 30cm. It is cut into 2 indentical squares, 2 identical rectangles and a shaded small square. Find the area of the shaded square.
Find the area of the shaded square.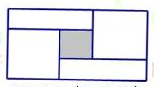
Answer: The area of the shaded square is ............... cm2.
A rectangle has a length of 60cm and a width of 30cm. It is cut into 2 indentical squares, 2 identical rectangles and a shaded small square. Find the area of the shaded square.
Find the area of the shaded square.
Answer: The area of the shaded square is ............... cm2.
Given P(x) = (x2 - 1/2 x - 1/2)1008
If P(x) = a2016x2016 + a2015x2015 + ..... + a1x + a0
then the value of the sum a0 + a2 + a4 + .... + a2014 is ...........
Given P(x) = (x2 - 1/2 x - 1/2)1008
If P(x) = a2016x2016 + a2015x2015 + ..... + a1x + a0
then the value of the sum a0 + a2 + a4 + .... + a2014 is ...........
Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây: